Градиент. Операторы Гамильтона (набла) и Лапласа

⇐ ПредыдущаяСтр 2 из 2

В этом вопросе устанавливается взаимосвязь между скалярным и векторным полем. Для простоты рассмотрим контурную карту местности (см. рис. 8, а), на которой изображена симметричная гора, поднимающаяся к вершине в центре карты (см. рис. 8, б). Высоты, нанесённые на контурную карту, представляют собой скалярные величины: каждая точка даёт высоту в определённое число метров. Когда все точки равных высот соединены между собой изолиниями, то в горизонтальной плоскости полностью определяется форма земной поверхности. Итак, на рис. 8, а) и б) изображено скалярное поле высот.

Для того, чтобы создать векторное поле поместим на склоне горы шар, и обозначим стрелками силу, удерживающую его от ската вниз (см. рис. 8, в). Этим самым определено векторное поле сил. При этом длина стрелки показывает величину удерживающей силы в различных точках, а направление стрелки – направленность силы. На некоторых географическим картах стрелки заменяются штриховым рисунком (см. рис. 8, г). Итак, на рис. 8, в) и г) изображено векторное поле сил, действующих на шар для его удержания.

Рис. 8 – Пример скалярного поля и его взаимосвязь с векторными полем

Для рассматриваемого случая связь между скалярным полем высот и векторным полем сил очень проста и хорошо известна: сила зависит от крутизны склона, или, другими словами, от степени изменения высоты с расстоянием. Эта величина изменения представляет собой производную по направлению, аналогичную по своему существу обычной производной, используемой в дифференциальном исчислении. Правда, усложнение заключается в необходимости определить направление крутизны склона, без чего нельзя найти направление, по которому шар будет стремиться скатываться. Наиболее крутой наклон в данной точке называют градиентом в этой точке. Градиент является вектором, и, следовательно, создаёт векторное поле.

Обобщим, данный вывод на электромагнитное поле. Электромагнитное поле в скалярном виде графически задается в виде эквипотенциальных поверхностей уровней в 3-х мерном пространстве либо эквипотенциальных линий уровня в 2-х мерном пространстве. Взаимное расположение поверхностей (линий) уровней позволяют судить о скорости изменения скалярного поля по тому или иному направлению, но только качественно. Количественную характеристику скорости изменения скалярного поля дает производная по направлению. Чем ближе расположены линии поля, тем круче наклон и тем больше градиент.

Производная скалярного поляU(x, y, z) по направлению, заданному вектором , вычисляется по формуле

, (21)

где , , 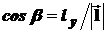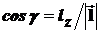– направляющие косинусы вектора .

Вектор единичной длины , совпадающий с вектором по направлению, имеет следующие координаты .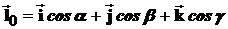

Абсолютная величина 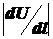производной по направлению определяет скорость изменения скалярного поля в точке M, а знак производной – характер ее изменения Если , то поля U(x, y, z) возрастает в данном направлении, если , то поле убывает.

Градиент скалярного поляU(М) есть вектор, направленный по нормали к поверхности уровня поля в сторону максимального возрастания поля и численно равный наибольшей производной по направлению. В таком определении градиент является инвариантной, т.е. не зависящей от выбора системы координат, характеристикой скалярного поля. Координатная формула для вычисления градиента имеет вид:

. (22)

При этом говорят, что в области V определено векторное поле градиентов.

Градиент является обобщением понятия первой производной функции одной переменной на случай функции трех переменных.

Отметим некоторые свойства градиента.

1) Производная по любому направлению равна скалярному произведению градиента на единичный вектор этого направления

.              (23)

здесь j– угол между единичным вектором направления и вектором gradU.

Используя это свойство, можно дать определение градиента, не зависящее от системы координат. Градиентом скалярного поля U(M) в точке М называется вектор, проекция которого на направление заданного единичного вектора равна производной поля U(M) по этому направлению

.                                         (24)

2) Производная по направлению принимает свое наибольшее значение в направлении градиента

.                      (25)

Модуль градиента показывает максимальную скорость изменения функции в окрестности точки М, то есть частоту линий уровня.

3) Вектор-градиент направлен по нормали к поверхности уровня в сторону возрастания функцииU(M).

Пусть на поверхности уровня задана произвольная кривая L, проходящая через точку М, в параметрическом виде задан радиус-вектор и его дифференциал , т.е. бесконечно малое смещение вдоль данной кривой из точки М, в которой вычисляется градиент gradU(см. рис. 9).

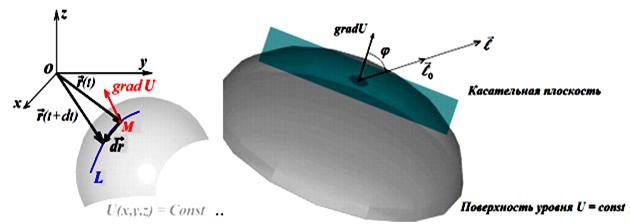
а)                                      б)

Рис. 9 – Вектор-градиент к поверхности уровня

Тогда из определения поверхности уровня dU = 0 следует

и .

Из произвольности выбора кривой L следует, что градиент в точке М ортогонален к любой кривой, лежащей на поверхности уровня и содержащей эту точку М, а значит, к самой поверхности уровня.

Из этого свойства непосредственно следует, что если U(M)=C – поверхность уровня в скалярном поле и (M) – единичная нормаль к этой поверхности уровня в точке М, то

,                                                    (26)

где знак + или – выбирается в зависимости от ориентации поверхности.

4) Если в области V градиент равен нулю (grad U=0), тоU = constant, т.е. скалярное поле постоянно вV.

5) Градиент обладает теми же дифференциальными свойства, что и дифференциал функции.

Действительно, если скалярное поле определено функцией f(u, v), где u и v – дифференцируемые скалярные поля, то

                               (27)

В частности, если f равно u + v, u v или u/v, то из (27) имеем

                               (28)

Рассмотрим пример. Найти градиент радиального поля U(x, y, z) = r, где

- модуль радиус-вектора .

Решение.

,

аналогично

, .

И тогда окончательно

.

Таким образом, градиент это векторная величина, показывающая степень изменения скалярного поля.

Для упрощения и ускорения записей уравнений векторного анализа ирландский математик Уильям Гамильтон ввел оператор в виде перевернутой греческой буквы дельты . В последствие этому оператору английский ученый Оливер Хэвисайд придумал название «набла» по аналогии с буквой финикийского алфавита. Кроме того, применение данного оператора позволяет легче запоминать уравнения векторного анализа.

Этот дифференциальныйвектор-оператор набла (Гамильтона) определяется как

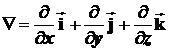.                                           (29)

Если формальное произведение понимать как производную , тогда

,                         (30)

т.е. произведение вектора-оператора ∇ на скаляр U(x, y ,z) даёт значение градиента поля U в точке M(x, y , z). Иначе говоря, действие оператора Гамильтона на скалярное поле генерирует векторное поле градиентов.

Через оператор «набла» естественным способом выражаются основные операции векторного анализа: grad(градиент), div(дивергенция), rot (ротор), а также оператор Лапласа.

Дифференциальным оператором Лапласа или лапласианом, обозначаемым D (большой греческой буквой дельта) называется дифференциальный оператор вида:

.                                           (31)

Этот оператор можно определить и как скалярный квадрат оператора набла, т.е. скалярное произведение оператора набла на себя:

. (32)

Оператор Лапласа – скалярный оператор, его применение к скалярному полю генерирует скаляр.

Пусть для скалярной функции U(x, y, z) определены частные производные второго порядка, тогда результат применения оператора Лапласа к этой функции записывается в следующем виде

. (33)

Также как в случае функции одной переменной U = U(x), геометрический смысл действия оператора Лапласа аналогичен геометрическому смыслу вычисления второй производной по направлению, что связано с понятиями выпуклости и кривизны графика функции (см. рис. 10).

Рис. 9 – Геометрический смысл оператора Лапласа

Если лапласиан ∆U < 0, тогда функция имеет выпуклость и поле имеет тенденцию расходиться из этой области (например, жидкость будет растекаться из области с максимальным напором), если ∆U > 0, то график функции имеет вогнутость и поле имеет тенденцию концентрироваться в этой области (например, жидкость будет стекаться к областям понижения рельефа). Если ∆U = 0, тогда скалярная функция поля не может достигать своих экстремальных значений ни в одной точке этой области. Уравнение ∆U = 0 называется уравнением Лапласа. Оно используется при описании различных установившихся процессов, например установившегося движения несжимаемой жидкости и др. Скалярные поляU(x, y, z), удовлетворяющие условию ∆U = 0, называются гармоническими, к ним относятся различного рода потенциалы – потенциал поля тяготения, электрического поля и др.

Таким образом, в данном вопросе установлено, что скалярные поля потенциала и векторные поля силы связаны между собой дифференциальным оператором градиентом, который математически представляет собой скалярное произведение векторного оператора набла на скалярную функцию поля. Для получения (определения) из скалярного поля другого скалярного поля применяется дифференциальный оператор Лапласа.

В электродинамике используется понятие градиента для определения напряженности электрического поля, которая равна минус градиент электрического потенциала.

Дата добавления: 2018-05-12; просмотров: 5078; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!