Понятия цифровой электроники. Логические операции. Логические элементы
Теоретической основой проектирования цифровых устройств является алгебра логики, или алгебра Д. Буля, оперирующая двумя логическими высказываниями «истинно» и «ложно», которые обозначаются соответственно символами 1 и 0.
Сложное высказывание называется логической функцией: y=f(x1,x2...xn), в которой сама функция y и ее аргументы - двоичные числа, принимаюшие значения 0 и 1. Наиболее часто в цифровых схемах применяются логические элементы, реализующие следующие логические функции:
Логические операции
1. Инверсия : 
Таблица истинности. Таблица истинности ставит в соответствие определенной комбинации входных переменных – заданное значение логической функции.
Таблица 10.1. Таблица истинности инвертора &
| X | Y |
| 0 | 1 |
| 1 | 0 |
2. Операция логического сложения или дизъюнкция: Y = X1 + X2
= X1UX2
Операция логического умножения или конъюнкция: Y = X1*X2 = X1&X2
1 Инвертор - реализует функцию логического отрицания или инверсии, которая часто обозначается как НЕ.


Логические функции могут задаваться различными способами, из которых мы будем использовать 3.
1) аналитическое представление функции (для НЕ - y =`x);
2) табличный способ, когда функция задается в виде таблицы истинности;
3) способ временных диаграмм.
 2 Логический элемент ИЛИ - реализует функцию логического сложения (дизъюнкция).
2 Логический элемент ИЛИ - реализует функцию логического сложения (дизъюнкция).
3 Логический элемент И - реализует функцию логического умножения (конъюнкция).
|
|
|

4 Логический элемент И-НЕ (Штрих Шеффера).

5 Логический элемент ИЛИ-НЕ (Стрелка Пирса).

Логический элемент – равнозначность (исключающее ИЛИ-НЕ).


7 Логический элемент - Исключающее ИЛИ (неравнозначность).

Мажоритарный логический элемент или схема голосования.
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
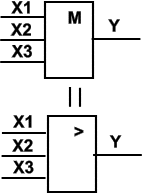
Y = 1, когда на входе единиц больше чем нулей.
Основные тождества алгебры Буля
Алгебра логики (АЛ) является основным инструментом синтеза и анализа дискретных автоматов всех уровней. АЛ называют также Булевой алгеброй. АЛ базируется на трёх функциях, определяющих три основные логические операции.
1. Функция отрицания (НЕ). f1 =`X читается, как f1 есть (эквивалентна) НЕ Х. Элемент, реализующий функцию НЕ, называется элементом НЕ (инвертором).

Элемент НЕ имеет два состояния.
2. Функция логического умножения (конъюнкции). Функция логического умножения записывается в виде f2=X1·X2. Символы логического умножения &, L, <×>, ´. Функция конъюнкции читается так: f2 есть (эквивалентна) Х1 и Х2, поскольку функция истинна тогда, когда истинны 1-й и 2-й аргументы (переменные). Конъюнкцию называют функцией И, элемент, реализующий эту функцию, элементом И.
|
|
|

В общем случае функцию логического умножения от n переменных записывают так:

Количество переменных (аргументов), участвующих в одной конъюнкции, соответствует количеству входов элемента И.
3. Логическое сложение (дизъюнкция). Функция логического сложения записывается в виде f3=X1 + X2, и читается так: f3 есть Х1 или Х2, поскольку функция истинна, когда истинна одна или другая переменная (хотя бы одна). Поэтому функцию дизъюнкции часто называют функцией ИЛИ. Символы логического сложения +,V.
В общем случае функция ИЛИ записывается:

Используя операции (функции) И, ИЛИ, НЕ можно описать поведение любого комбинационного устройства, задав сколь угодно сложное булево выражение. Любое булево выражение состоит из булевых констант и переменных, связанных операциями И, ИЛИ, НЕ.
Пример булева выражения:
 .
.
Основные законы алгебры логики. Основные законы АЛ позволяют проводить эквивалентные преобразования функций, записанных с помощью операций И, ИЛИ, НЕ, приводить их к удобному для дальнейшего использования виду и упрощать запись.
ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ Таблица 1.1
|
|
|
| N | а | б | Примечание |
| 1 2 3 4 5 | 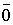 =1
X+0=X
X+1=1
X+X=X
X+ =1
X+0=X
X+1=1
X+X=X
X+  =1 =1
|  =0
X*1=X
X*0=0
X*X=X
X* =0
X*1=X
X*0=0
X*X=X
X*  =0 =0
| Аксиомы (тождества) |
| 6 |  =X =X
| Закон двойного отрицания | |
| 7 | X+Y=Y+X | X*Y=Y*X | Закон коммутативности |
| 8 | X+X*Y=X | X  =X =X
| Закон поглощения |
| 9 |  = =  * * 
| 
| Правило де-Моргана (закон дуальности) |
| 10 |  +Z=X+Y+Z +Z=X+Y+Z
| 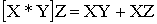
| Закон ассоциативности |
| 11 | X+  *Z= X+ Z *Z= X+ Z
| 
| Закон дистрибутивности |
Булевой алгебре свойственен принцип двойственности, что наглядно иллюстрирован в табл. 1.1. Как следует из табл. 1.1, только закон двойного отрицания не подчиняется этому принципу.
Используя законы алгебры логики, можно упростить булевы выражения, в частности, правило склеивания позволяет упростить выражение типа
 .
.
Действительно, используя законы 2, 5 и 11 можно записать исходное выражение в виде Х2(Х1 +`Х1 ) =Х2. Так как логическая операция Х1 +`Х1 = 1 (см. з-н 5), а Х2×1 = Х2 (см. з-н 2б), полученное выражение истинно.
Системы исчисления
В дискретной автоматике и вычислительной технике числовая информация представляется в двоичной системе счисления, при этом двоичные переменные можно рассматривать как элементы двоичного кода числа, то есть как цифры этой системы счисления. Двоичная система счисления, как и десятичная, относится к позиционным системам и является системой с основанием 2. В десятичной системе число А, имеющее n-разрядную целую часть и m-разрядную дробную часть, представляется суммой:
|
|
|
А=an-110n-1+an-210n-2+¼+ai10i+¼+a0100+a-110-1+a-210-2+¼+a-m10-m,
где ai - десятичная цифра от 0 до 9, а основанием системы счисления является число 10. Например, число 236.75 в десятичной системе счисления в соответствии с этим уравнением можно записать: 236.75=2×102+3×101+6×100+7×10-1+5×10-2.
Аналогично, в двоичной системе счисления число В можно представить в виде суммы
В=bn-12n-1+bn-22n-2+¼+bi2i+¼+b020+b-12-1+b-22-2+¼+b-m2-m,
где bi - двоичные цифры 0 и 1, а основанием системы счисления является число 2 (в десятичном виде). Например, то же число 236.75 в двоичном коде запишется: 236.75=1×27+1×26+1×25+0×24+1×23+1×22+0×21+0×20+1×2-1+1×2-2
Разумеется, для одного и того же числа А, количество разрядов в двоичной системе существенно больше, чем в десятичной. Например, трехразрядное десятичное число 235 в двоичной системе представляется восемью разрядами: 11101011. Перевод целой части числа из десятичной системы в двоичную производится методом последовательного деления числа на 2 до тех пор, пока частное от деления не станет равным единице, например:
| 42 | 2 | ||||
| 42 | 21 | 2 | |||
| 0 | 20 | 10 | 2 | ||
| 1 | 10 | 5 | 2 | ||
| 0 | 4 | 2 | 2 | ||
| 1 | 2 | 1 | |||
| 0 |
При этом число в двоичной системе числения записывается в виде остатков от деления, начиная с последнего частного, справа налево.В рассмотренном примере: 42 (10) = 101010 (2).
Для перевода дробной части числа последовательно умножаем дробную часть на два.
| 0 | 6875 |
| X2 | |
| 1 | 375 |
| X2 | |
| 0 | 75 |
| X2 | |
| 1 | 5 |
| X2 | |
| 1 | 0 |
Двоичное число записывается в виде целых частей чисел, полученных при умножении только дробной части, начиная сверху после запятой. В рассматриваемом примере (0,6875) (10) = 0,1011(2).
По рассмотренным правилам числа можно переводить и в другие системы счисления, например в восьмеричную, шестнадцатеричную и т. д., во всех случаях умножение или деление производится на основание новой системы счисления. Для представления чисел в любой системе счисления с основанием р используется набор из р символов: для р=2 – (0,1), для р=8 – (0,1,2,3,4,5,6,7), для р=10 – (0,...,9), для р=16 – (0,...,9,A,B,C,D,E,F).
Правила перевода из восьмеричной и шестнадцатеричной систем в двоичную систему: переводим по порядку все символы - цифры, затем нули слева и справа в записи двоичного числа отбрасываем. Пример:
725,54Q = (111 010 101, 101 100) = 111010101,1011B
Обратный перевод из двоичной системы:
Для перевода в восьмеричную систему: разбиваем двоичное число на группы по 3 разряда, начиная от запятой вправо и влево, добавляем недостающие нули слева и справа.
Аналогично для перевода из двоичной в шестнадцатеричную разбиваем на группы по 4 разряда. Пример: 1110101101,10111B = (001 110 101 101,101 110) = 1655,56Q
1110101101,10111B = (0011 1010 1101,1011 1000) = 3AD,B8H
Перевод числа из одной системы исчисления в другую и наоборот.
Двоичная система исчисления
516=5*10²+1*10¹+6*10º
Перевод чисел из двоичной системы в десятичную:

Дата добавления: 2018-05-12; просмотров: 623; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
