Линейная интерполяция методом ЦДА
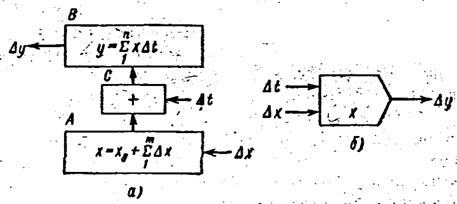
Рис. 6. Структурная схема (а) и схемное обозначение (б) интегратора цифрового дифференциального анализатора
Применение ЦДА основано на приближении
 ,
,
где 
Интегратор стоит из двух регистров и управляемого сумматора
(рис 6 а). Импульсом Dt содержимое регистра А (вели чина x) переносится в регистр В, что соответствует умножению Dtx. При заполнении регистра В возникает сигнал переноса Dу. Начальное значение.х0 предварительно устанавливается, в регистр А. Сочетание нескольких интеграторов, обеспечивает решение задачи интерполяции отрезка прямой и окружности, пронзи вольно расположенной в пространстве. -
Для движения по отрезку прямой I с постоянной результирующей скоростью v получим (рис. 7,а)

Рис. 7 - Отрезок прямой в пространстве (в) я блок-схема интерполятора (б)
 ;
;  ;
;  ;
;
 ;
; 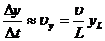 ;
;  ;
;
 ;
;  ;
;  ;
;
где cos a = xL/L; cos b = yL/L; cos g = zL/L.
Эта система уравнений решается интеграторами по схеме (рис. 7б).
Конец интерполяции определяется по сопоставлению выданного числа импульсов с величинами xL , yL , zL , хранящимися в памяти устройства.
Круговая интерполяция методом ЦДА
Окружность в пространстве, образованная пересечением сферы К с плоскостью Е, может быть задана уравнением радиус-вектора R

Рис. 8 - Окружность в пространстве (а) и блок-схема интерполятора (б)
Вектор скорости движения v по окружности определится векторным произведением угловой скорости на вектор R:
|
|
|
 ,
,
где wx= |w| cos aE; wy= |w| cos bE; wx= |w| cos gE; xR, yR ,zR - проекции вектора R на оси координат.
Для окружности в плоскости Е с радиусом R1 получим следующую систему уравнений при движении с постоянной скоростью v =  :
:
 ;
;
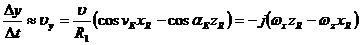 ;
;
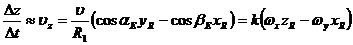 ;
;
Эта система уравнений решается ЦДА по блок-схеме на Начальные значения слагающих вектора R по координатным осям устанавливаются в блоках памяти ЦДА. Трехкоординатная интерполяция окружности является частным случаем объемной сферической интерполяции. Если окружность лежит в плоскости X - Y, то v£ = 0, и система уравнений и схема интерполятора (рис. 9, а) упрощается:
 ;
;
 ;
;

Рис.9 - Блок-схема кругового интерполятора в плоскости X-Y (а) и линейно-кругового интерполятора (б):
Л и К - сигналы на включение линейной или круговой интерполяции; Б - логический блок, задающий линейную или круговую ннтерполяцию
Объемная линейная и плоскостная круговая интерполяция могут выполняться общей схемой с определенными логическими переключениями (рис. (9, б). При интерполяции дуга окружности делится на п сегментов с угловым шагом  (рис.10).
(рис.10).
Определим погрешность интерполя ции. Уравнения окружности перед первым шагом и после него
|
|
|
x2+y2 = R2;
(x+  x)2+(y+
x)2+(y+  y)2 = R12.
y)2 = R12.

Рис.10 – Определение ошибки круговой интерполяции
Учитывая равенства
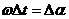 ;
;  ;
; 
 ;
; 



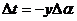 ,
,
получим после первого и после n-го шага
R2[1=(  )2] = R12 ;
)2] = R12 ;
R2[1=(  )2]n = Rn2,
)2]n = Rn2,
при 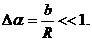
Раскладывая в ряд и пренебрегая членами высшего порядка, получим
Rn 
Для квадранта с  получим погрешность радиуса
получим погрешность радиуса

В пределе дуга bравна дискрете перемещения, и погрешность
ради уса соответствует R  0,79 дискрет.
0,79 дискрет.
Дата добавления: 2018-04-15; просмотров: 823; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
