Поняття про форму і розміри Землі.
Земля не є правильним геометричним тілом, її фізична поверхня, особливо поверхня суші надзвичайно складна. Поверхня Землі, яку прийнято називати фізичною, або топографічною, є поєднанням поверхні океанів і материків із складними геометричними формами. Океани займають майже три чверті площі планети, а нерівності суші незначні порівняно з її площею, тому форма Землі визначається поверхнею Світового океану. Це підтверджують і зйомки Землі з космічних літальних апаратів.
Поверхня океану в стані повного спокою і рівноваги є рівневою поверхнею, тобто поверхнею, на якій потенціал сили тяжіння Землі має однакове значення. Рівнева поверхня може бути проведена через будь-яку точку фізичної поверхні Землі, а також над або під поверхнею (рис. 4.1). Середній рівень Балтійського моря, відмічений межею Кронштадтського футштока, в нашій державі прийнятий за початкову рівневу поверхню, від якої відлічують висоти точок земної поверхні. Поверхня, що визначає форму планети й збігається з поверхнею Світового океану, називається основною.
Під загальною фігурою Землі в геодезії розуміють фігуру, яка уявлено обмежена під сушею поверхнею Світового океану в спокійному стані. Цю поверхню називають основною рівневою поверхнею, або поверхнею геоїда.
Рівневу поверхню гравітаційного поля Землі, яка співпадає з середнім рівнем води в океанах називають геоїдом, й приймають за математичну поверхню Землі або «рівень води», від якого відлічують висоту точок земної поверхні.
|
|
|
Для геодезичних вирахувань беруть правильну математичну фігуру, яка найбільш наближена до геоїда – сфероїд.
Сфера (математичний термін) – замкнута поверхня, всі точки якої однаково віддалені від однієї точки (центра сфери).
Відрізок, який з’єднує центр сфери з будь-якої її точкою, а також його довжину, називають радіусом сфери.
Сфероїд – стиснутий еліпсоїд обертання малого стискання (будь-яка поверхня близька до сфери).
Форма Землі, утворена рівневою поверхнею, що збігається з поверхнею Світового океану в стані цілковитого спокою і рівноваги й продовжена під материками, називається геоїдом.
Сучасні дослідження показали, що форма Землі формується під впливом внутрішніх і зовнішніх сил. Основними є сила внутрішнього тяжіння і відцентрова сила. За даними геофізики Земля поводиться як пластичне тіло. Якби вона була нерухомим і однорідним по щільності тілом, то під дією лише сил внутрішнього тяжіння вона, як фігура рівноваги, мала б форму кулі.
Насправді внутрішня будова Землі за щільністю неоднорідна і земна кора (зовнішній шар землі завтовшки в середньому 40 км.) складається з неоднорідних за щільністю ділянок: материки і океанічні западини складних геометричних форм, рівнинні і гірські форми рельєфу материків і океанів, що межують з ними. Внаслідок такого нерівномірного розподілу мас в земній корі змінюються напрями сил притягання, а отже, сил тяжіння і прямовисних ліній. Як результат поверхня геоїда, залишаючись у кожній точці перпендикулярною до прямовисних ліній, набуває складної і неправильної в геометричному відношенні форми, яку неможна описати кінцевим математичним виразом (рис.4.3). Прямовисними лініями називаються лінії, які збігаються з напрямком дії сили тяжіння і перпендикулярні до рівневої поверхні в будь-якій її точці.
|
|
|
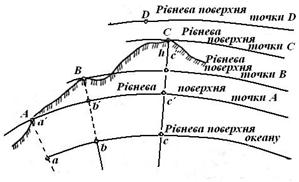
Рис. 4.1. Рівневі поверхні
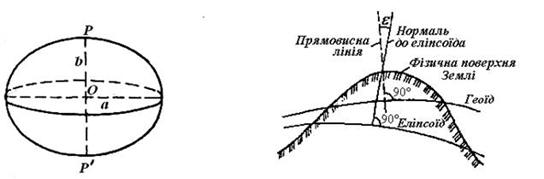
Рис. 4.2. Земний еліпсоїд та його елементи. Рис. 4.3. Відхилення прямовисної лінії.
Для математичної обробки результатів геодезичних вимірів потрібно знати форму поверхні Землі. Використовувати для цієї мети фізичну поверхню або поверхню геоїда не можна внаслідок їх складності. Оскільки найбільші відхилення геоїда від еліпсоїда (еліпсоїд – фігура, утворена обертанням еліпса довкола малої осі внаслідок дії відцентрової сили) не перевищують 100 – 150 м, фігурою, найбільш близькою до геоїда, є еліпсоїд обертання, що називається земним еліпсоїдом. Напрямки прямовисної лінії і нормалі в точках земної поверхні не збігаються (рис. 4.3) і утворюють кут відхилення прямовисної лінії ε. В середньому його значення становить 3 – 4", а в місцях аномалій досягає десятків секунд. Нормалі, це лінії, перпендикулярної до поверхні еліпсоїда.
|
|
|
Параметрами, що визначають розміри і форму земного еліпсоїда, є велика а і мала b півосі і величина відносного стиску 
(рис. 4.2). Величини цих параметрів можуть бути отримані за допомогою градусних вимірів, тобто шляхом геодезичних вимірів довжини дуги меридіана в 1°. Знаючи довжину градуса в різних місцях меридіана, можна визначити фігуру і розміри Землі.
За даними градусних вимірювань вчені Деламбр (1800), Бессель (1841), Хейфорд (1909) та ін. розрахували розміри земних еліпсоїдів. Параметри еліпсоїда, обчислені вченими ЦНДІГАіК під керівництвом Ф. Н. Красовського (1940), такі: а = 6378245м, b = 6356863м, α = 1:298,3. В 1946 р. ці розміри затверджені як обов’язкові для проведення геодезичних і картографічних робіт в СРСР. В інженерній геодезії фігуру Землі приймають за кулю радіусом 6371,11км.
Дата добавления: 2018-04-15; просмотров: 876; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!