Свободные колебания при линейно – вязком сопротивлении

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Рассмотрим движение материальной точки под действием восстанавливающей силы и силы сопротивления , пропорциональной скорости точки. Составим дифференциальное уравнение движения

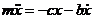
и приведем его к виду

, где 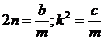. (1.8)

Предположим, что его решение должно иметь вид

. (1.9)

Для проверки правильности предположения найдем выражения для и подставим их и (1.9) в (1.8). Вынося общий множитель за скобку, имеем

Полученное произведение равно нулю, если . Это означает, что сделанное предположение (1.9) справедливо. Однако характер движения будет зависеть от соотношения величин и .

1. Пусть . Тогда - действительные отрицательные числа и решение будет иметь вид

. (1.10)

Характер возможных движений в этом случае представлен на рис.1.5; движение является апериодическим, экспоненциальным, что говорит о большом сопротивлении.

Рис.1.5

2. Пусть 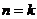. Тогда - действительные отрицательные числа и решение будет иметь вид

(1.11)

Характер движения аналогичен представленному на рис.1.5.

3. Пусть . Тогда - комплексные числа и решение может быть приведено, с помощью формулы Эйлера для преобразования комплексных величин, к виду

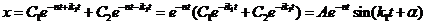. (1.12)

Характер процесса затухающих колебаний представлен на рис.1.6.

Рис.1.6

Период затухающих колебаний

(1.13)

несколько больше периода свободных колебаний, а последовательность амплитуд представляет в этом случае убывающую геометрическую прогрессию, знаменатель которой называется декрементом колебаний. Его величина будет

, (1.14)

где и - амплитуды -го и - го колебания (см. рис. 1.6).

В некоторых задачах используется модуль его натурального логарифма; он называется логарифмическим декрементом колебаний .

В тех случаях, когда сила сопротивления пропорциональна скорости в степени выше первой (например, ), дифференциальное уравнение нелинейно, а его решение не может быть записано в виде аналитической зависимости. По результатам численного решения такого уравнения строится график (при большом сопротивлении график похож на рис.1.5; при малом – на рис.1.6, однако интервалы времени между наибольшими отклонениями и отношения соседних отклонений не будут постоянны).

Иногда на практике приходится иметь дело с обратной задачей, когда по записи процесса колебательного движения необходимо сделать вывод о структуре силы сопротивления. Алгоритм действий следующий: во-первых, измеряются интервалы времени между наибольшими отклонениями. Если интервалы одинаковы, то сила сопротивления является либо силой сухого трения, либо силой линейно – вязкого сопротивления. Во-вторых, измеряются наибольшие отклонения от средней линии; если они образуют арифметическую прогрессию, преобладает сухое трение, а если геометрическую, то линейно-вязкое. В противном случае действует сила сопротивления, пропорциональная скорости точки в степени выше первой.

ПРИМЕР 3. ([9]). Для определения вязкости жидкости Кулон употреблял следующий метод: подвесив на пружине тонкую пластинку, он заставлял ее колебаться сначала в воздухе, а затем в той жидкости, вязкость которой надлежало определить, и находил продолжительность одного размаха: - в первом случае и - во втором. Сила трения между пластинкой и жидкостью может быть выражена формулой 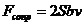, где - площадь пластинки, - ее скорость, - коэффициент вязкости. Пренебрегая трением между пластинкой и воздухом, определить коэффициент по найденным из опыта величинам и , если масса пластинки .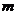

РЕШЕНИЕ. Изобразим на рис.1.7 пластинку в сосуде с жидкостью и нанесем силы, на нее действующие.

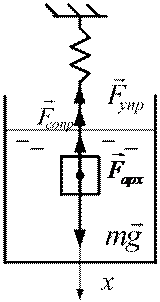
Рис.1.7

Если начало координаты 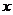поместить в положение статического равновесия, то проекция уравнения движения пластинки на ось 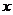будет совпадать с уравнением (1.8).

При колебаниях в воздухе пренебрежем силой Архимеда и силой сопротивления 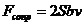, тогда дифференциальное уравнение движения будет совпадать с уравнением (1.1). Дифференциальное уравнение движения пластинки, полностью погруженной в линейно-вязкую жидкость, совпадает с (1.8). Эти обстоятельства позволяет воспользоваться полученными выше формулами.

Возведем в квадрат выражение для периода затухающих колебаний и учтем, что частота свободных колебаний может быть выражена через период как . Тогда получим выражение

где . После несложных преобразований находим

1.4. Вынужденные колебания материальной точки при действии гармонического возбуждения.

В некоторых случаях кроме восстанавливающей силы может действовать возмущение, которое является заданной функцией времени. Возмущение бывает силовым (на рис.1.8.а к точке приложена переменная сила), кинематическим (на рис.1.8.б точка подвеса двигается по заданному закону) или инерционным (на рис.1.8.в возмущение обусловлено вращением неуравновешенной массы ;).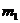

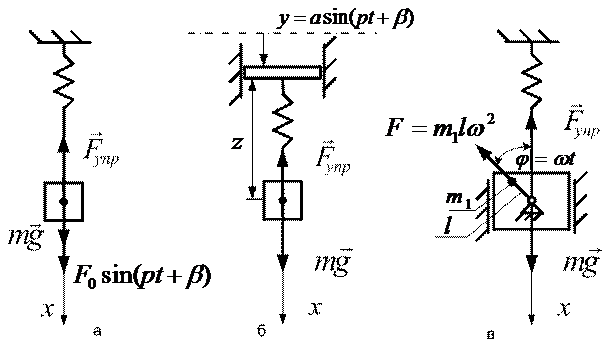Рис.1.8

Рассмотрим наиболее распространенный случай, когда возмущающая сила изменяется по гармоническому закону, т.е. . Дифференциальное уравнение в этом случае можно записать так:

Оно может быть переписано в виде

, (1.15)

где - известные константы.

Это неоднородное дифференциальное уравнение второго порядка, решение которого есть сумма решений однородного уравнения (1.1) и частного решения уравнения (1.15). В случае, когда , последнее находится достаточно просто. Если предположить, что его вид , где - неизвестные постоянные, то после подстановки выражений для 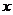и в неоднородное уравнение (1.15), получим

В результате общее решение неоднородного уравнения запишется как

. (1.16)

Как уже говорилось выше, постоянные интегрирования и могут быть определены из начальных условий. В общем случае искомое движение будет включать гармонические колебания трех типов: первые два будут происходить с частотой свободных колебаний , при этом амплитуда первых будет зависеть от начальных условий, а вторых - от параметров вынуждающего воздействия; колебания третьего типа будут происходить с частотой изменения вынуждающей силы, а их амплитуда не будет зависеть от начальных условий.

Колебания первого типа называют свободными, второго – сопутствующими, а третьего – вынужденными.

Остановимся подробнее на последнем слагаемом (в технических приложениях эти колебания называют вибрацией). Введем величину , представляющую смещение точки при действии на нее постоянной силы . Величина отношения амплитуды вынужденных колебаний к этому смещению показывает, во сколько раз динамическое отклонение превосходит ; эта величина называется коэффициентом динамичности и определяется как .

Зависимость коэффициента динамичности от отношения , по сути, представляет собой в безразмерном виде, зависимость амплитуды вынужденных колебаний от частоты вынуждающего воздействия. В дальнейшем под словами амплитудно-частотная характеристика мы будем подразумевать графическое изображение функции , а зависимость отставания смещения от вынуждающей силы – фазово-частотной характеристикой. Графики этих характеристик для силового гармонического возбуждения колебаний приведены на рис.1.9.а и 1.9.б соответственно.

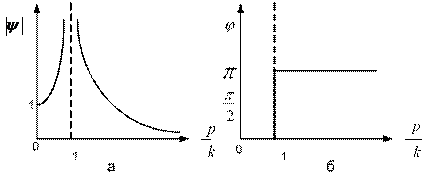
Рис.1.9

Анализ амплитудно-частотной характеристики показывает, что при стремлении частоты вынуждающей силы к нулю, амплитуда вынужденных колебаний стремится к величине статического отклонения; при бесконечно большой частоте вынуждающей силы амплитуда вынужденных колебаний стремится к нулю; при совпадении частоты вынуждающей силы и собственной частоты амплитуда вынужденных колебаний может стать бесконечно большой (явление резонанса). Анализ фазово-частотной характеристики показывает, что смещение и вынуждающая сила до резонанса совпадают по направлению; после резонанса их направления противоположны.

Явление резонанса. Кратко коснемся ситуации, когда 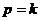. Частное решение уравнения (1.15) в этом случае следует искать в виде . Подставив это выражение в (1.15), получаем два соотношения

Отсюда , . Окончательно получим

. (1.17)

График этой зависимости (при нулевых начальных условиях) приведен на рис.1.10.

Рис.1.10

Как видно, при 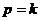происходит неограниченное возрастание амплитуды вынужденных колебаний, причем рост амплитуды линейно зависит от времени. Из этого факта следует важный вывод: если рабочая частота механизма находится за частотой резонанса, последнюю следует проходить быстро (чтобы амплитуда вынужденных колебаний не успела достигнуть опасных значений, вызывающих разрушение механизма).

Явление биений. В случае, когда частота близка к собственной частоте , благодаря наложению колебаний наступает своеобразное явление, называемое биением. Опуская выкладки (при желании с ними можно ознакомиться, например, в [4]), для вынужденных колебаний получаем зависимость

. (1.18)

График этого движения представлен на рис.1.11.

Рис.1.11

Показанные здесь биения представляют собой колебания, происходящие с частотой вынуждающей силы, причем амплитуда этих колебаний медленно меняется, следуя также периодическому закону. Чем ближе величина к собственной частоте , тем больше амплитуда биений и период ее изменения; при 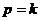биения переходят в резонанс. После прохода резонанса вновь возникают биения, исчезающие с ростом частоты вынуждающего воздействия.

Кинематическое возбуждение. Если к одному из концов пружины жесткости прикрепить груз массы 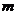, а другой конец заставить совершать вертикальные гармонические колебания (см. рис.1.8.б) по закону , то такое возбуждение колебаний называют кинематическим.

Очевидно, что рассмотрение этого примера в неподвижной координатной системе приводит к дифференциальному уравнению

где 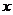- смещение груза в неподвижной координатной системе, - растяжение пружины в положении статического равновесия.

Записанное уравнение совпадает с (1.15) при . Очевидно, что все сказанное выше, будет справедливо и для этого случая.

Если нас интересует движение груза по отношению к движущемуся концу пружины (т.е. относительное движение груза), то, согласно [4], к силам, действующим на груз, следует добавить силу инерции переносного движения

Рассмотрение задачи в подвижной координатной системе приводит к дифференциальному уравнению

совпадающему с (1.15) при .

Коэффициент динамичности в этом случая характеризует отношение амплитуды вынужденных колебаний к амплитуде кинематического возбуждения:

. (1.19)

Амплитудно-частотная и фазово-частотная характеристики движения для этого случая приведены на рис.1.12а и 1.12.б соответственно.

Рис.1.12

Очевидно, что при вынужденные колебания отсутствуют; с ростом частоты кинематического возбуждения амплитуда вынужденных колебаний растет, пока частота не достигнет области резонанса; при дальнейшем возрастании частоты кинематического возбуждения амплитуда вынужденных колебаний стремиться к амплитуде кинематического возбуждения, при этом кинематическое возбуждение и вынужденные колебания происходят в противофазе (т.е. ).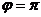

Связь решений в неподвижной и подвижной координатных системах обусловлена (см. рис. 1.8.б) соотношением

ПРИМЕР 4. Виброметр используется для определения амплитуд вертикальных колебаний частей машины. В подвижной системе прибора демпфер отсутствует. Собственная частота колебаний виброметра – 6 Гц. В каком диапазоне должна находиться частота исследуемой вибрации, чтобы погрешность измерения ее амплитуды не превышала 5%?

РЕШЕНИЕ. Очевидно, что в рассматриваемом примере имеет место кинематическое возбуждение колебаний. Из рис.1.12.а и формулы (1.19) видно, что при амплитуда вибрации стремиться к амплитуде кинематического возбуждения. Очевидно, что в таком случае показания виброметра будут наиболее точно регистрировать колебания объекта, на котором он установлен; при этом кинематическое возбуждение и относительное движение груза будут в противофазе (т.е. ).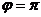

Воспользуемся формулой (1.19) для расчета амплитуды вибрации и выразим из нее отношение . Потребуем, чтобы величина этого отношения отличалась от 1 (их точное совпадение) не более, чем на 5%, т.е. была бы равна 1.05. Тогда на границе искомого диапазона должно выполняться равенство

Выполнив расчет, получим, что

Из графика 1.11.а видно, что и в дорезонансной области существуют частоты вибрации, где соотношение

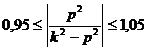
выполняется, однако конструировать виброметр для работы в столь узком диапазоне частот не имеет смысла.

Инерционное возбуждение. Если вынужденные колебания обусловлены вращением неуравновешенной массы 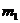(см. рис.1.8.в), то такое возбуждение колебаний называется инерционным.

В этом случае к действующим силам следует добавить центробежную силу инерции , и учесть ее вертикальную составляющую

Очевидно, что вынужденные колебания при инерционном возбуждении будут аналогичными рассмотренным выше колебаниям в подвижной системе отсчета при кинематическом возбуждении.

Полигармоническое возбуждение. В случае, когда вынуждающая сила представляет собой полигармоническое воздействие (например, ; - целое число), в силу линейности задачи решение 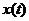может быть получено в виде суммы из решений, в каждом из которых рассматривается действие только одного моногармонического воздействия, т.е. .

Дата добавления: 2018-04-04; просмотров: 434; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 Следующая ⇒

Мы поможем в написании ваших работ!