Средняя квадратич.ошибка весового среднего
Средние квадратические ошибки неравноточных измерений различны, поэтому для оценки точности таких измерений выбирают общую меру. Такой мерой является средняя квадратическая ошибка такого измерения, вес которого равен единице.Следует отметить, что величина М (средняя квадратическая ошибка веса) может относится к воображаемому измерению, если среди результатов нет ни одного с весом равным единице.  .Установим связь между средней квадратической ошибкой единицы веса М и средней квадратической ошибкой результата измерений с весом :
.Установим связь между средней квадратической ошибкой единицы веса М и средней квадратической ошибкой результата измерений с весом :
 . Если имеем ряд неравноточных измерений с весами P1, P2, P3 и средней квадратической ошибкой m1, m2,...,mn, то для каждого результата измерений ошибки веса будут равны:
. Если имеем ряд неравноточных измерений с весами P1, P2, P3 и средней квадратической ошибкой m1, m2,...,mn, то для каждого результата измерений ошибки веса будут равны:
 .Среднее квадратическое значение из этого ряда будет:
.Среднее квадратическое значение из этого ряда будет: 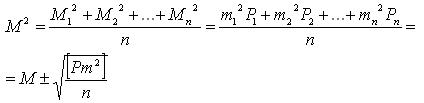 . Если заменить m на ∆ или δ, то получим соответственно:
. Если заменить m на ∆ или δ, то получим соответственно:
 . Эту формулу можно применять для связи ошибки весового среднего М0 с весом [P] и ошибкой единицы веса М, то есть можно записать:
. Эту формулу можно применять для связи ошибки весового среднего М0 с весом [P] и ошибкой единицы веса М, то есть можно записать:
 .
.
2.Метод наименьших квадратов – один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке геодезических измерени.
Метод наименьших квадратов содержит в себе 2 основных способа: коррелатный и параметрический, которые при строгом уравнивании дают одинаковые результаты. Выбор способа обычно зависит от объема вычислений, определяемого в основном количеством совместно решаемых уравнений, т.е. конфигурацией сети. Коррелатный способ более оптимален для свободных сетей и сетей с небольшим числом исходных пунктов и большим числом определяемых – по-скольку количество уравнений равно числу избыточных измерений. Параметрический способ, наоборот, выгоден для сетей с большим числом исходных и малым числом определяемых, по-скольку количество уравнений будет равно числу необходимых измерений.
|
|
|
Идея коррелатного способа заключается в отыскании поправок к измеренным величинам через вспомогательные неопределенные множители, называемые коррелатами. Сущность уравнивания коррелатным способом состоит в том, что задачу нахождения минимума функции уравнения разложенного по ряду Тейлора решают по способу Лагранжа с определеннымикоррелатами, в результате чего получают коррелатные уравнения поправок (векторы поправок). Преобразовав уравнения поправок получают нормальные уравнения коррелат, через которые находят вероятнейшие значения поправок.
Параметрический способ подразумевает вычисление поправок не к измеренным величинам, а к каким-то приближенным значениям (параметрам), т.е. к конечным результатам уравнения, которыми в геодезических сетях являются координаты или высоты пунктов, и непосредственное получение вероятнейших значений параметров, минуя вероятнейшее значение измеренных элементов сети.
|
|
|
Метод наименьших квадратов был предложен К. Ф. Гауссом (1794-95) и А. Лежандром (1805-06). Первоначально этот метод использовался для обработки результатов астрономических и геодезических наблюдений. Строгое математическое обоснование и установление границ содержательной применимости метода наименьших квадратов даны А. А. Марковым и А. Н. Колмогоровым. Ныне способ представляет собой один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.
Задача Ганзена.
Из всех известных способов рассмотрим способ условных координат.Решение задачи этим способом состоит в решении прямой однократной засечки по видоизмененным формулам Юнга. При этом сначала определяют условные координаты точек  и
и  , а затем их условные координаты перевычисляют в систему координат точек
, а затем их условные координаты перевычисляют в систему координат точек  и
и  .Примем точку
.Примем точку  за начало условных координат
за начало условных координат  , а направление
, а направление  – за положительное направление оси ординат (рис.1). Расстояние
– за положительное направление оси ординат (рис.1). Расстояние  условно примем равным, например, 1000.000 м. Тогда условные координаты точек
условно примем равным, например, 1000.000 м. Тогда условные координаты точек  и
и  будут:
будут: 



 Рис.1.Задача Ганзена (условная система координат). По видоизмененным формулам Юнга из треугольников
Рис.1.Задача Ганзена (условная система координат). По видоизмененным формулам Юнга из треугольников  и
и  найдем условные координаты точек
найдем условные координаты точек  и
и  :
:  ,
,  .
.
|
|
|
По условным координатам точек  и
и  можно определить условный дирекционный угол
можно определить условный дирекционный угол  из решения обратной геодезической задачи, после чего отыскать все углы, образуемые направлениями с точек
из решения обратной геодезической задачи, после чего отыскать все углы, образуемые направлениями с точек  и
и  на точки
на точки  и
и  как разности дирекционных углов соответствующих направлений:
как разности дирекционных углов соответствующих направлений:  (1),
(1), 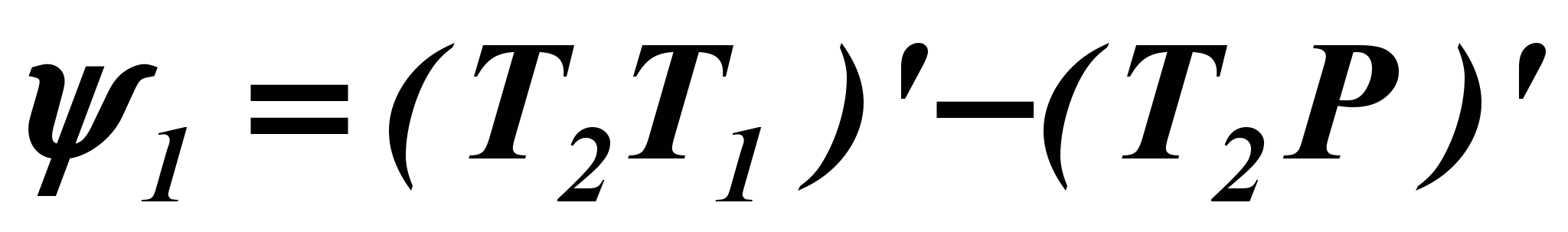 (2),где
(2),где  ,
,  .
.  – исходный условный дирекционный угол направления
– исходный условный дирекционный угол направления  ,
,  и
и  – вычисленные исходные дирекционные углы направлений
– вычисленные исходные дирекционные углы направлений  и
и  .В отыскании углов при точках
.В отыскании углов при точках  и
и  и состояла цель введения условных координат. Определив указанные углы далее по действительным координатам точек
и состояла цель введения условных координат. Определив указанные углы далее по действительным координатам точек  и
и  из треугольника найдем искомые координаты точки
из треугольника найдем искомые координаты точки  :
:  .Координаты точки
.Координаты точки  определяются из треугольника
определяются из треугольника  либо из треугольника
либо из треугольника  , поскольку в обоих треугольниках углы известны. Точность определения координат искомой пары пунктов зависит от величины углов четырехугольника, образованного двумя исходными и двумя определяемыми точками. Наибольшая точность обеспечивается в случае, если образованный четырехугольник по своей форме близок к квадрату.
, поскольку в обоих треугольниках углы известны. Точность определения координат искомой пары пунктов зависит от величины углов четырехугольника, образованного двумя исходными и двумя определяемыми точками. Наибольшая точность обеспечивается в случае, если образованный четырехугольник по своей форме близок к квадрату.
|
|
|
Билет 3
1. Поверка и юстировка коллимационной ошибки у теодолита 3Т5КП
Теодолит 3Т5КП – оптический прибор со шкаловым отсчетным микроскопом самоустанавливающимся компенсатором вертикального круга. Визирная ось зрительной трубы V-V должна быть перпендикулярна к оси вращения трубы III-III.Угол с отклонения визирной оси от перпендикуляра к оси вращения трубы называется коллимационной ошибкой. Для выявления коллимационной ошибки выбирают удаленную, хорошо видимую точку, расположенную так, чтобы линия визирования была примерно горизонтальна. Наводят трубу на эту точку при положении вертикального круга справа от трубы и берут отсчет по горизонтальному кругу (  ). Переведя трубу через зенит, то есть повернув трубу на 180° в вертикальной плоскости, наводят ее на ту же точку и снова берут отсчет (
). Переведя трубу через зенит, то есть повернув трубу на 180° в вертикальной плоскости, наводят ее на ту же точку и снова берут отсчет (  ). Величина коллимационной ошибки найдется как
). Величина коллимационной ошибки найдется как  (1)Если величина ошибки будет превышать удвоенную точность отсчетного устройства прибора, вычисляют среднее из минут, полученных при
(1)Если величина ошибки будет превышать удвоенную точность отсчетного устройства прибора, вычисляют среднее из минут, полученных при  и
и  , и устанавливают средний отсчет с помощью наводящего винта алидады. При этом произойдет смещение перекрестия сетки нитей относительно изображения наблюдаемого предмета. Ослабив предварительно вертикальные винты сетки нитей, боковыми винтами передвигают сетку до точного совмещения перекрестия с изображением предмета. Для контроля поверку повторяют.При поверках оптических теодолитов с односторонним отсчитыванием (ТЗО, Т15 и др.) для исключения влияния эксцентриситета определение коллимационной ошибки делается дважды с поворотом лимба после первого определения на 180°. Величину коллимационной ошибки в этом случае вычисляют по формуле
, и устанавливают средний отсчет с помощью наводящего винта алидады. При этом произойдет смещение перекрестия сетки нитей относительно изображения наблюдаемого предмета. Ослабив предварительно вертикальные винты сетки нитей, боковыми винтами передвигают сетку до точного совмещения перекрестия с изображением предмета. Для контроля поверку повторяют.При поверках оптических теодолитов с односторонним отсчитыванием (ТЗО, Т15 и др.) для исключения влияния эксцентриситета определение коллимационной ошибки делается дважды с поворотом лимба после первого определения на 180°. Величину коллимационной ошибки в этом случае вычисляют по формуле  (2)
(2)
Для устранения коллимационной ошибки в этом случае вычисляют отсчет, исправленный за величину ошибки  (3)
(3)  (4)и устанавливают этот отсчет с помощью наводящего винта алидады. Смещение сетки нитей с точки устраняют также боковыми исправительными винтами сетки нитей.
(4)и устанавливают этот отсчет с помощью наводящего винта алидады. Смещение сетки нитей с точки устраняют также боковыми исправительными винтами сетки нитей.
2.Определить среднюю квадратическую ошибку функции вида: Р=0,5 a*bsin  , если a=50м
, если a=50м  ; b=100м
; b=100м  ;
;  ,
, 
Решение :  ,
,  ,
,  .
. 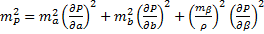 ,
,  ,
, 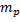 =
=  =1,4
=1,4
Дата добавления: 2018-04-04; просмотров: 819; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
