Часть1: Расчет электростатического поля сферического конденсатора
Санкт-Петербургский государственный политехнический университет
Институт энергетики и транспортных систем
Кафедра «Теоретические основы электротехники»
К У Р С О В О Й П Р О Е К Т
Расчеты электромагнитных полей и электромагнитных параметров
Электротехнических устройств
по дисциплине «Теоретические основы электротехники»
Выполнил
Студент группы 33213/1 П.Д.Никитин
Руководитель
доцент, к.т.н. А.Н.Модулина
«_____» _____________________2014 г.
Санкт-Петербург
2014 г.
Санкт-Петербургский государственный политехнический университет
ЗАДАНИЕ
НА ВЫПОЛНЕНИЕ КУРСОВОГО ПРОЕКТА
студенту группы 33213/1Никитину П.Д.
1. Тема проекта:Расчеты электромагнитных полей и электромагнитных параметров электротехнических устройств
2. Срок сдачи студентом законченного проекта 17 декабря 2014 г.
3. исходные данные к проекту:
3.1. Сферический конденсатор;
3.2 Линейный провод, распложенный вблизи проводящего экрана;
3.3. Устройство с ферромагнитным сердечником.
4. Содержание пояснительной записки:
4.1. Введение;
4.2. Основная часть.
4.2.1. Расчет электростатического поля сферического конденсатора, сечение которого изображено на рис. Z-1
 Рис. Z-1
Рис. Z-1
|
1. Вывести выражения потенциала и напряженности электростатического поля в пространстве между обкладками сферического конденсатора (см. рис.Z-1) с радиусами R1=2,5 см и R2=6 см, построить графики полученных зависимостей U(r) и E(r) в случаях, когда:
|
|
|
1.1. между электродами помещена двухслойная изоляция с абсолютными диэлектрическими проницаемостями слоев  =9 e0 и
=9 e0 и  , радиус поверхности раздела слоев диэлектрика равен R12=4 см, внутренняя обкладка конденсатора подключена к источнику ЭДС с напряжением U0=300 В, внешняя заземлена (U2=0);
, радиус поверхности раздела слоев диэлектрика равен R12=4 см, внутренняя обкладка конденсатора подключена к источнику ЭДС с напряжением U0=300 В, внешняя заземлена (U2=0);
1.2. двухслойная изоляция заменена однородным диэлектриком с проницаемостью  , замена произведена при подключенном к внутреннему электроду источнике ЭДС;
, замена произведена при подключенном к внутреннему электроду источнике ЭДС;
1.3. двухслойная изоляция заменена однородным диэлектриком с проницаемостью  , замена произведена после отключения внутреннего электрода от источника ЭДС.
, замена произведена после отключения внутреннего электрода от источника ЭДС.
Во всех рассмотренных случаях определить полные заряды q каждого из электродов и поверхностную плотность зарядов s на них.
2. Полагая напряжение между электродами u12=U1–U2 фиксированным и равным U0, получить и построить зависимости напряжений слоев диэлектрика uI=U1–U12 и uII=U12–U2, максимальной напряженности поля Emax, зарядов q каждого из электродов и поверхностной плотности зарядов s на них, а также емкости системы C от e1.
|
|
|
3. Определить оптимальное значение диэлектрической проницаемости e2 внешнего слоя изоляции, при котором максимальные величины напряженности во внутреннем и внешнем слоях диэлектрика одинаковы.
4.2.2. Расчет плоскопараллельного электростатического поля между линейным заряженным проводом и проводящим экраном
| а) | б) |

| 
|
Рис. Z-2
Провода несимметричной трехфазной системы расположены в однородной среде с диэлектрической проницаемостью e0 вблизи проводящего экрана. Минимальное расстояние от провода до экрана равно d. Один из проводов (1), показанный на рис.Z-2,а, имеет линейный заряд t, заряды проводов 2 и 3, расположенных относительно 1-го в соответствии с рис.Z-2,б, равны нулю. Радиусы проводов одинаковы и равны R=0,1d.
1. Построить картину плоскопараллельного электростатического поля, создаваемого 1-м проводом (см. рис.Z-2,а). При построении картины поля радиусом провода пренебречь. Принять число линий равного потенциала, включая границу, n=5 и число трубок потока вектора напряженности m= 9. Определить распределение индуцированного заряда s по поверхности экрана.
2. Рассчитать емкость 1-го провода относительно экрана на единицу длины системы. Сопоставить полученное значение емкости с емкостью
|
|
|
а) такого же провода, расположенного на расстоянии d от плоской проводящей поверхности,
б) цилиндрического конденсатора с радиусом внутренней жилы R1=R, внутренним радиусом оболочки R2=d и диэлектрической проницаемостью диэлектрика e0.
3. Определить величины потенциалов каждого из проводов трехпроводной линии, принява=3, b= 4.
4. Определить емкость провода трехфазной транспонированной линии на единицу ее длины.
4.2.3. Расчет магнитного поля и определение параметров устройства с ферромагнитным сердечником

a= 6; b= 8; c= 20; d=2; f=4; g=10
Рис. Z-3
Плоскопараллельное магнитное поле создается в межполюсном пространстве системой обмоток, обтекаемых током i = 1 А, витки которых w = 100 равномерно распределены по сечению (рис. Z-3,а).
1. Принимая магнитную проницаемость материала сердечника mFe = ∞ и положив толщину обмотки t=0, построить картину магнитного поля, используя:
а) графический метод;
б) результат расчета «вручную» распределения скалярного магнитного потенциала методом конечных разностей.
2. С помощью программы “POLUS” выполнить расчет распределения скалярного магнитного потенциала и функции потока и построить картины полей для толщины обмотки t = 0; t=a/2 и t=a. По построенным картинам полей определить индуктивность обмотки. Построить зависимость индуктивности от ширины обмотки L(t). Размеры магнитной системы в сантиметрах приведены на рис. Z-3,б.
|
|
|
4.3. Заключение.
4.4. Список использованных источников.
4.5. Приложения.
5. Перечень графического материала:
5.1. Графики распределения потенциала и напряженности между обкладками конденсатора во всех рассмотренных случаях; зависимости напряжений слоёв, максимальной напряженности, зарядов электродов q1,2 и поверхностной плотности заряда s на них, ёмкости C от диэлектрической проницаемости e1; распределение напряженности вдоль радиуса при оптимальном значении диэлектрической проницаемости e2;
5.2. Картина электрического поля между проводом и заземленным проводящим экраном в канонической области Dw и в области Dz; распределение индуцированного заряда по поверхности экрана;
5.3. Картины магнитного поля, полученные указанными в п. 4.2.3 способами при заданных значениях ширины обмотки; зависимость индуктивности от ширины обмотки.
5.4. Презентационные материалы к защите.
6. Консультанты доц., д.т.н. Калимов А.Г.
7. Дата получения задания 6 октября 2014 г.
Руководитель доц., к.т.н.Модулина А.Н.
Задание принял к исполнению ________________ Никитин П.Д.
(подпись студента)
________________
(дата)
Содержание
Введение. 7
Часть1: Расчет электростатического поля сферического конденсатора. 8
Часть 2: Расчет плоскопараллельного электростатического поля между линейным заряженным проводом и проводящим экраном. 29
Часть 3: Расчет магнитного поля полюса с обмоткой. 43
Заключение. 54
Список использованных источников. 55
Введение
Часть1: Расчет электростатического поля сферического конденсатора
 Вывести выражение потенциала и напряженности электростатического поля в пространстве между обкладками сферического конденсатора с радиусами
Вывести выражение потенциала и напряженности электростатического поля в пространстве между обкладками сферического конденсатора с радиусами  и
и  . Между электродами помещена двуслойная изоляция с абсолютными диэлектрическими проницаемостями слоев
. Между электродами помещена двуслойная изоляция с абсолютными диэлектрическими проницаемостями слоев  и
и  , радиус поверхности раздела слоев диэлектрика равен
, радиус поверхности раздела слоев диэлектрика равен  , внутренняя обкладка конденсатора подключена к источнику ЭДС с напряжением
, внутренняя обкладка конденсатора подключена к источнику ЭДС с напряжением 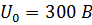 , внешняя заземлена (
, внешняя заземлена ( 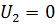 ).
).





Нахождение потенциала и напряжённости электростатического поля по заданному распределению потенциала – задача, обратная основной задаче электростатики. Она решается с помощью уравнения Лапласа и граничных условий. Для сферического конденсатора решим уравнение Лапласа:
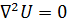

В силу того, что потенциал в сферическом конденсаторе не зависит от угла φ и θ, частные производные по этим углам будут равны нулю, следовательно





Где 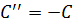
В различных областях сферического конденсатора распределения потенциала будет описываться различными уравнениями:
Для R1<r
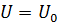
Для R1<r<R12

Для R12<r<R2

Для определения постоянных интегрирования используем граничные условия
На границе 

На границе 


На границе 

Таким образом,система уравнений имеет вид:

Решая полученную систему, найдем:




Зная выражение для потенциала, несложно найти выражение для напряженности электростатического поля:

Для R1<r

Для R1<r<R12

Для R12<r<R2

В итоге мы получили следующие значения напряженности и потенциала в зависимости от расстояния:
Для R1<r

Для R1<r<R12

Для R12<r<R2

Найдем полные заряды q каждого электрода и поверхностную плотность заряда σ на них.
На первом электроде:


На втором электроде:


График потенциала для задания 1.1

График напряженности для задания 1.1

Вывести выражение потенциала и напряженности электростатического поля в пространстве между обкладками сферического конденсатора с радиусами  и
и  . Двуслойная изоляция заменена однородным диэлектриком с проницаемостью
. Двуслойная изоляция заменена однородным диэлектриком с проницаемостью  , замен произведена при подключенном к внутреннему электроду источнике ЭДС
, замен произведена при подключенном к внутреннему электроду источнике ЭДС




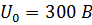
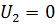
Решение в этом случае такое же, как в пункте 1.1 – нахождение потенциала и напряжённости электростатического поля по заданному распределению потенциала с помощью уравнения Лапласа и граничных условий. Воспользуемся решенным уравнением Лапласа

И рассмотрим распределения потенциала в двух областях:
Для R1<r
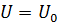
Для R1<r<R2

И два граничных условия:
1) 
2) 
Таким образом, система уравнений имеет вид:

Решив систему уравнений из граничных условий нашли постоянные:


Снова найдем выражения для напряженности электростатического поля:

Для R1<r
 Для R1<r<R2
Для R1<r<R2
 И, подставив константаны, запишем выражения для напряженности и потенциала в конечно форме:
И, подставив константаны, запишем выражения для напряженности и потенциала в конечно форме:
Для R1<r

Для R1<r<R2

Найдем полные заряды q каждого электрода и поверхностную плотность заряда σ на них.
На первом электроде:
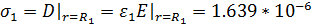

На втором электроде:


График потенциала для задания 1.2

График напряженности для задания 1.2

Вывести выражение потенциала и напряженности электростатического поля в пространстве между обкладками сферического конденсатора с радиусами  и
и  . Двуслойная изоляция заменена однородным диэлектриком с проницаемостью
. Двуслойная изоляция заменена однородным диэлектриком с проницаемостью  , замена произведена после отключения внутреннего электрода от источника ЭДС.
, замена произведена после отключения внутреннего электрода от источника ЭДС.
Замена двуслойного диэлектрика на однородный происходит в три этапа:
А)Внутренний электрод подключен к источнику ЭДС, между обкладками двуслойный диэлектрик. Такая задача уже решена в пункте 1.1, и были получены следующие значения поверхностной плотности зарядов:


Б)Электрод отключен от источника ЭДС, ничего не изменилось.
В)Двуслойный диэлектрик заменен однородным диэлектриком с проницаемостью 
Воспользовавшись условием сохранения заряда на отключенном внутреннем электроде, мы можем сказать, что
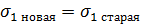
И, следовательно,решить прямую основную задачу электростатики – найти напряженность поля во всех точках, зная заряд.
Потенциал будет описываться новым уравнением с новыми константами:
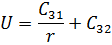
И напряженность соответственно

Новая поверхностная плотность заряда

Для определения постоянной интегрирования C31 используем условие сохранения поверхностной плотности заряда на внутреннем электроде s1новая = s1старая. Таким образом:

Поскольку электрод отключен, значит напряжение на границе  , и мы можем найти константу
, и мы можем найти константу 


Выражения для потенциала и напряженности в конечной форме:

Полные заряды q каждого электрода и поверхностная плотность заряда σ на них будет такая же, как и в задании 1.1.
На первом электроде:


На втором электроде:


График потенциала для задания 1.3

График напряженности для задания 1.3

Полагая напряжение между электродами  фиксированным и равным
фиксированным и равным  , получить и построить зависимости напряжений слоев диэлектрика
, получить и построить зависимости напряжений слоев диэлектрика 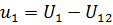 и
и  , максимальной напряженности поля
, максимальной напряженности поля  , зарядов q каждого из электродов и поверхностной плотности зарядов σ на них, а также емкости системы С от
, зарядов q каждого из электродов и поверхностной плотности зарядов σ на них, а также емкости системы С от  .
.
Нам известно, что  ,
, 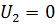
Следовательно,для первого слоя диэлектрика

Потенциал для R1<r<R12 равен:

Из системы уравнений для определения постоянных интегрирования, полученной в пункте 1.1 выразим зависимость 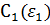


Подставив  в уравнение напряженности, при фиксированном радиусе
в уравнение напряженности, при фиксированном радиусе  , получим:
, получим:

В итоге зависимость напряжения  в первом слое диэлектрика имеет вид:
в первом слое диэлектрика имеет вид:

График этой зависимости выглядит так:

Для второго слоя диэлектрика

Потенциал для R12<r<R2 равен:
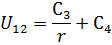
Из системы уравнений для определения постоянных интегрирования, полученной в пункте 1.1 выразим зависимость  и
и 


Подставив  и
и  в уравнение напряженности, при фиксированном радиусе
в уравнение напряженности, при фиксированном радиусе  , и, подставив в зависимость напряжения
, и, подставив в зависимость напряжения  во втором слое диэлектрика, получим:
во втором слое диэлектрика, получим:


Эта зависимость имеет следующий вид:
Напряженность поля  в области первого диэлектрика (R1<r<R12) будет описываться уравнением:
в области первого диэлектрика (R1<r<R12) будет описываться уравнением:

А в области второго диэлектрика (R12<r<R2):

Изобразив на одном графике зависимость  , мы получим график максимальной напряженности поля
, мы получим график максимальной напряженности поля 

Максимальная напряженность:

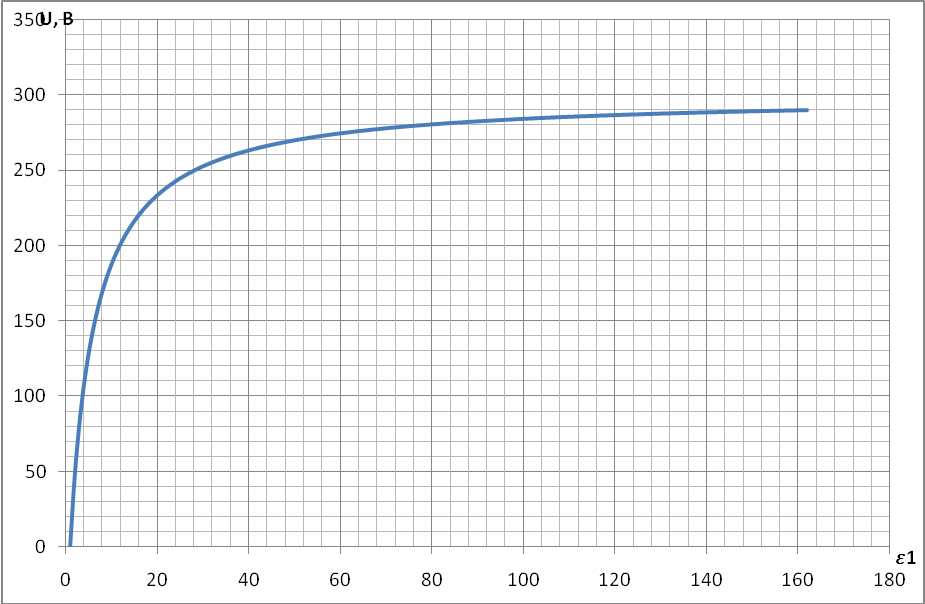
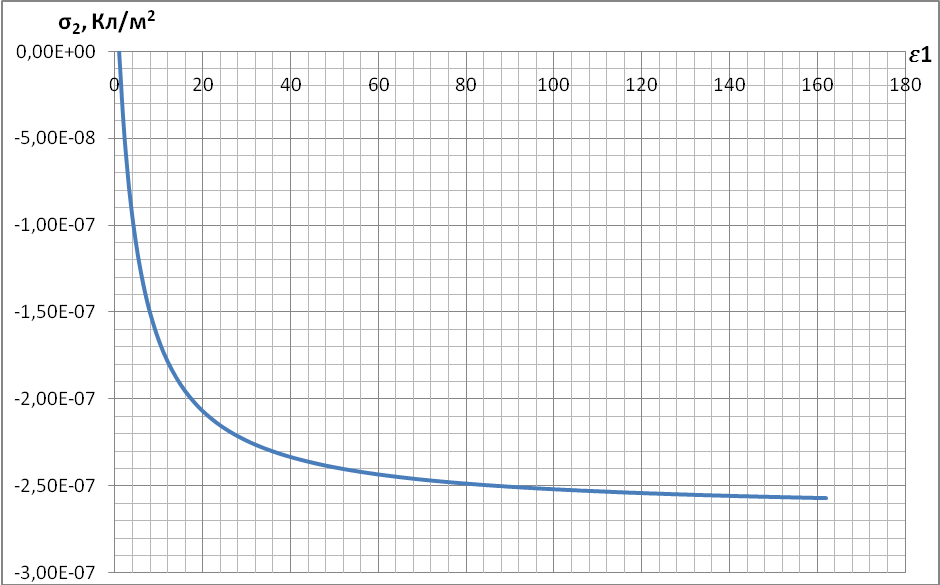
Поверхностная плотность зарядов σ1 и σ2 зависит от  следующим образом:
следующим образом:


Ниже представлены графики этих зависимостей:

Зависимости зарядов q каждого из электродов от 


Их графики выглядят следующим образом:


Зависимость емкости системы  от
от  рассчитаем по формуле:
рассчитаем по формуле:

Зависимость имеет вид:

Определить оптимальное значение диэлектрической проницаемости  внешнего слоя изоляции, при котором максимальные величины напряженности во внутреннем и внешнем слоях диэлектрика одинаковы.
внешнего слоя изоляции, при котором максимальные величины напряженности во внутреннем и внешнем слоях диэлектрика одинаковы.



Из системы уравнений для определения постоянных интегрирования, полученной в пункте 1.1 выразим зависимость  и
и 


Значение абсолютной диэлектрической проницаемости первого слоя  , второго слоя
, второго слоя  .Для того, чтобы максимальные величины напряженности во внутреннем и внешнем слоях диэлектрика были одинаковы, необходимо изменить
.Для того, чтобы максимальные величины напряженности во внутреннем и внешнем слоях диэлектрика были одинаковы, необходимо изменить  до значения
до значения  .
.



 При новом значении
При новом значении  график напряженности имеет вид:
график напряженности имеет вид:
Дата добавления: 2018-04-05; просмотров: 2033; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
