Сложение гармонических колебаний

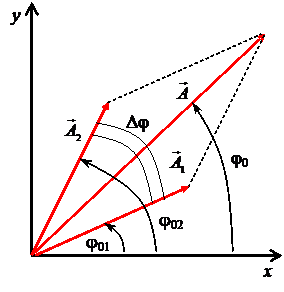
 При сложении гармонических колебаний одинакового направления и одинаковой частоты обычно используется метод векторных диаграмм.

Согласно методу векторных диаграмм, каждому колебанию может быть поставлен в соответствие некоторый вектор, например вектор  (рисунок 7), вращающийся относительно своего начала с угловой скоростью, равной циклической частоте ω0 этого колебания.

Модуль такого вектора равен амплитуде соответствующего колебания, а его проекция на выбранное направление, например, на ось х (рисунок 7), будет совершать гармонические колебания:

,

где φ – угол между вектором  и осью координат х в момент времени t.

Обозначив проекцию А_х через х, получим уравнение гармонических колебаний:

.

При сложении двух гармонических колебаний одинакового направления и одинаковой циклической частоты, происходящих, например, вдоль оси х, первое из которых описывается уравнением:

,

а второе - уравнением

,

где х₁, х₂ - смещения; А₁, А₂ - амплитуды; , - начальные фазы соответствующих колебаний; t - время, результирующее колебание будет происходить также вдоль оси х с той же циклической частотой ω₀ в соответствии с уравнением

.

При этом амплитуда результирующего колебания А и тангенс начальной фазы φ0 в последнем уравнении находятся методом векторных диаграмм и определяются в соответствии с рисунком 8 по формулам:   ,   .

Сложение взаимно-перпендикулярных колебаний

При сложении двух гармонических колебаний одинаковой циклической частоты ω₀, происходящих в двух взаимно-перпендикулярных направлениях, например, вдоль осей координат х и у, определяемых соответственно уравнениями:

,

,

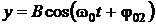где х и у - смещения; А и В - амплитуды; ,  - начальные фазы;             t - время, уравнение результирующего колебания будет иметь вид:

.

Затухающие механические колебания

     Свободные колебания, амплитуда которых уменьшается с течением времени вследствие потерь энергии в окружающую среду, называются затухающими.

     Уравнение затухающих механических колебаний имеет следующий вид:

,

где  х- смещение, А₀ - начальная амплитуда в момент времени, равный нулю;         

β - коэффициент затухания, который определяется коэффициентом сопротивления r и массой m колеблющейся материальной точки:

;

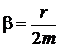
ω- частота затухающих колебаний:

,

где t - время; - начальная фаза колебаний.

     Период затухающих колебаний

.

Как следует из уравнения затухающих колебаний и рисунка 9, амплитуда А затухающих колебаний (пунктирная линия на рисунке 9) экспоненциально  уменьшается с течением времени:

Время τ, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Учитывая, что амплитуда затухающих колебаний спустя время, равное времени релаксации

,

Получим, исходя из определения времени релаксации, что

Поэтому время релаксации

.

     Следовательно, время релаксации обратно пропорционально коэффициенту затухания β.

Величина, равная натуральному логарифму отношения значений амплитуд, соответствующих моментам, отличающимся по времени на период, называется логарифмическим декрементом затухания:

.

То есть

.

Следовательно, логарифмический декремент затухания возрастает при увеличении коэффициента затухания β и периода Т  колебаний.

Мы поможем в написании ваших работ!