Частина II. Коливання і хвилі
Основні закони і співвідношення
· Рівняння гармонічного коливання має вигляд
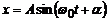
або
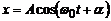 ,
,
де: x – зміщення коливної точки (чи центра мас тіла) від положення рівноваги; А – амплітуда; t – час; a – початкова фаза; w0 – циклічна частота власних незгасаючих коливань (власна циклічна частота).
· Частота (лінійна)
 ,
,
період коливань
 ,
,
де N – число коливань за час t.
· Зв’язок циклічної частоти з періодом
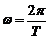 .
.
· Формули для розрахунку періоду вільних незгасаючих механічних коливань різних осциляторів:
а) пружинного маятника
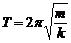 ;
;
б) математичного маятника
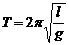 ;
;
в) фізичного маятника
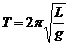 .
.
Тут: m – маса маятника (у випадку а) – це маса матеріальної точки чи тіла, прикріпленого до пружини); k – жорсткість пружини; l – відстань від центра мас маятника до точки підвісу (у випадку б) ця величина співпадає з довжиною нитки); g – прискорення вільного падіння; L – зведена довжина фізичного маятника;
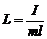 ,
,
де І – момент інерції маятника відносно осі, що проходить через точку підвісу перпендикулярно до площини коливань центра мас.
· У випадку фізичного маятника рівняння коливань прийнято записувати через кут відхилення j від положення рівноваги (кутове зміщення)
 .
.
· Кінетична енергія осцилятора
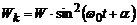 ,
,
Потенціальна енергія
 ,
,
Повна механічна енергія
 .
.
· При складанні двох однаково направлених гармонічних коливань однакової частоти одержується гармонічне коливання тієї ж частотиз амплітудою
|
|
|
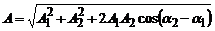
та з початковою фазою a, що задовільняє рівняння
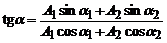 .
.
Тут A1 і A2 – амплітуди вихідних коливань, a1 та a2 – початкові фази.
· При складанні двох взаємно перпендикулярних гармонічних коливань однакової частоти рівняння траєкторії результуючого руху має вигляд
 ,
,
А – амплітуда коливання по осі Ох, В – по осі Оу.
· Рівняння згасаючих коливань
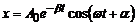 ,
,
де: А0 – амплітуда при  ; b – коефіцієнт згасання, w – циклічна частота згасаючих коливань,
; b – коефіцієнт згасання, w – циклічна частота згасаючих коливань,
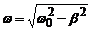 .
.
· Логарифмічний декремент згасання
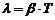 .
.
· Рівняння усталених вимушених коливань
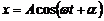 ,
,
де: w – циклічна частота зовнішньої періодично діючої сили;
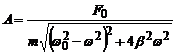 ;
;
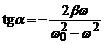 ;
;
F0 – амплітудне значення змушувальної сили.
· Резонансна частота
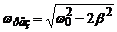 .
.
· Рівняння плоскої хвилі, що поширюється вздовж осі Ох:
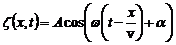
або
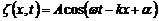 ,
,
де: 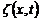 – зміщення коливної точки в момент часу t в точці простору з координатою х; А – амплітуда коливань; w – циклічна частота; v – модуль фазової швидкості хвилі; a – початкова фаза;
– зміщення коливної точки в момент часу t в точці простору з координатою х; А – амплітуда коливань; w – циклічна частота; v – модуль фазової швидкості хвилі; a – початкова фаза;  – хвильове число;
– хвильове число; 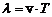 – довжина хвилі; Т – період коливань.
– довжина хвилі; Т – період коливань.
· Модуль швидкості звуку в рідині
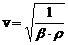 ,
,
де r – густина, b – адіабатична стисливість рідини.
· Модуль швидкості поширення звуку в газах (близьких до ідеального)
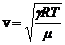 ,
,
де g – коефіцієнт Пуасона (показник адіабати), R – універсальна газова стала, m – молярна маса, Т – абсолютна температура.
|
|
|
· Закони зміни з часом заряду на обкладках конденсатора  та різниці потенціалів між обкладками
та різниці потенціалів між обкладками  в реальному коливальному контурі за формою однакові, адже U та q є прямо пропорційними величинами(
в реальному коливальному контурі за формою однакові, адже U та q є прямо пропорційними величинами( 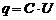 , С – електроємність):
, С – електроємність):
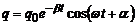 ,
,
 ,
,
де коефіцієнт згасання коливань 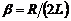 , R – активний опір котушки, L – її індуктивність,
, R – активний опір котушки, L – її індуктивність, 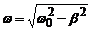 ,
, 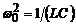 , q0 і U0 – значення qmax та Umax при t = 0, причому
, q0 і U0 – значення qmax та Umax при t = 0, причому 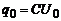 .
.
Закон зміни сили струму  запишемо лише для ідеального контура (R = 0):
запишемо лише для ідеального контура (R = 0):
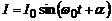 ,
,
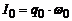 . Період коливань в такому контурі
. Період коливань в такому контурі
 .
.
· Період електромагнітних коливань в реальному контурі
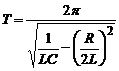 .
.
· У випадку вимушених електромагнітних коливаньрезонанс напруг наступає, якщо циклічна частота зовнішньої періодичної напруги наближається до резонансної частоти контура  , а резонанс струмів при
, а резонанс струмів при 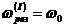 .
.
· Рівняння плоскої електромагнітної хвилі, що поширюється вздовж осі Ох
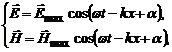
де:  та
та  – напруженості електричного і магнітного полів хвилі,
– напруженості електричного і магнітного полів хвилі,  та
та 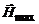 – амплітуди відповідних величин.
– амплітуди відповідних величин.
· Зв’язок модулів напруженостей E і H
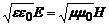 ,
,
де: 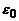 та
та  – електрична і магнітна сталі; e та m – діелектрична і магнітна проникності середовища.
– електрична і магнітна сталі; e та m – діелектрична і магнітна проникності середовища.
· Модуль швидкості поширення електромагнітних хвиль
|
|
|
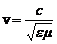 ,
,
 – електродинамічна стала. Оскільки v залежить від середовища, то й довжина хвилі різна в різних середовищах (період коливань і, відповідно, частота незмінні).
– електродинамічна стала. Оскільки v залежить від середовища, то й довжина хвилі різна в різних середовищах (період коливань і, відповідно, частота незмінні).
· Інтенсивність електромагнітної хвилі
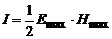 .
.
Приклади розв’язування задач
Приклад 1.Матеріальна точка масою m = 5 г здійснює гармонічні коливання з частотою n0 = 0,5 Гц. Амплітуда коливань А = 3 см. Визначити: 1) модуль швидкості v точки в момент часу, коли зміщення x = 1,5 см; 2) максимальне значення модуля діючої сили Fmax; повну енергію W точки.
Розв’язання
| Дано: m = 5 г n0 = 0,5 Гц А = 3 см х = 1,5 см |
| v ? Fmax ? W ? |
Рівняння гармонічних коливань має вигляд
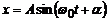 ,
,
де w0 – власна циклічна частота, a – початкова фаза коливань. Продиференціювавши це рівняння, отримаємо вираз для проекції вектора швидкості
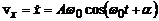 .
.
Щоб пов’язати цю величину зі зміщенням, заданим в умові задачі, піднесемо обидва виписані рівняння до квадрату і додамо одержані вирази:
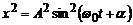 ,
,
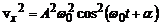 ,
,
 .
.
Звідси 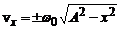 .
.
Врахуємо тепер зв’язок циклічної частоти з лінійною 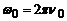 і вираз модуля вектора через його проекції, котрий в одновимірному випадку зводиться до
і вираз модуля вектора через його проекції, котрий в одновимірному випадку зводиться до 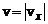 . Остаточно маємо
. Остаточно маємо
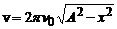 .
.
|
|
|
Щоб розрахувати величину Fmax, запишемо другий закон Ньютона у проекціях на напрям вектора прискорення 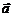 :
:
 .
.
Проекцію прискорення знайдемо як похідну по часу від проекції швидкості
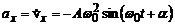 .
.
Тепер
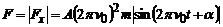 .
.
Очевидно, що  , якщо
, якщо 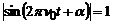 , тому остаточно
, тому остаточно
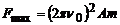 .
.
Повну механічну енергію коливної точки розраховують за формулою  , отже
, отже
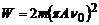 .
.
Виписуємо тепер значення величин в міжнародній системі одиниць і виконуємо числовий розрахунок:
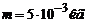 ;
; 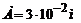 ;
;  ;
;
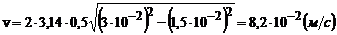 ;
;
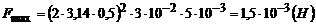 ;
;
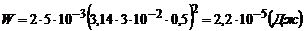 .
.
Відповідь:  ,
, 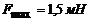 ,
, 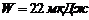 .
.
Приклад 2. Записати рівняння коливання, отриманого при складанні двох однаково направлених гармонічних коливань 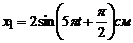 та
та 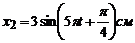 .
.
Розв’язання
Дано:
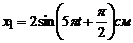
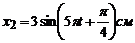
|
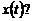
|
Результатом додавання двох гармонічних коливань однакової частоти та однакового напрямку є теж гармонічне коливання тієї ж частоти і того самого напрямку:
 ,
,
де амплітуда А розраховується за формулою
 ,
,
а початкова фаза a знаходиться з рівняння
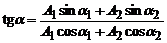 .
.
Величини А1, А2, a1, a2 та w0 маємо з порівняння загального вигляду рівняння гармонічних коливань і рівнянь з умови задачі:
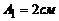 ,
, 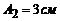 ,
, 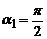 ,
, 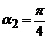 ,
, 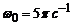 .
.
Маємо
 ,
,
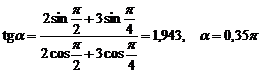 .
.
Тепер рівняння результуючого коливання
 .
.
Відповідь:  .
.
Приклад 3. Матеріальна точка одночасно бере участь у двох взаємно перпендикулярних гармонічних коливаннях, рівняння яких  та
та 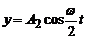 , де
, де  ,
, 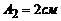 ,
,  . Знайти рівняння траєкторії точки. Побудувати траєкторію з дотриманням масштабу.
. Знайти рівняння траєкторії точки. Побудувати траєкторію з дотриманням масштабу.
Розв’язання
Дано:

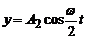

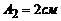

|
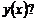
|
Щоб знайти рівняння траєкторії (рівняння, що пов’язує змінні x та y), виключимо час t з рівнянь, що задані в умові. Для цього використаємо формулу 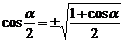 . У нас
. У нас  , тому маємо
, тому маємо
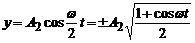 .
.
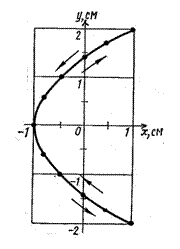 Але з першого рівняння умови задачі
Але з першого рівняння умови задачі 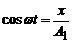 , тому остаточно маємо рівняння траєкторії
, тому остаточно маємо рівняння траєкторії
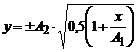 .
.
Це – рівняння параболи, вісь якої співпадає з віссю Ох. З вихідних рівнянь умови задачі бачимо, що зміщення точки по осях координат обмежене, а саме: 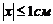 ,
,  .
.
Для побудови траєкторії знайдемо за робочою формулою значення у, що відповідають ряду значень х з інтервалу 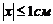 , і складемо таблицю:
, і складемо таблицю:
| х, см | -1 | -0,75 | -0,5 | 0 | +0,5 | +1 |
| у, см | 0 | ±0,707 | ±1 | ±1,41 | ±1,73 | ±2 |
Побудуємо тепер графік.
Відповідь: 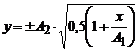 .
.
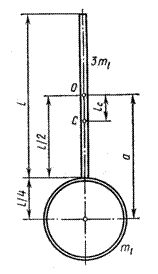
Приклад 4. Дано фізичний маятник у формі стрижня довжиною l = 1 м і масою 3m1 з прикріпленим до одного з його кінців обручем діаметром d = 0,5 l і масою m1. Горизонтальна вісь Oz маятника проходить через середину стрижня перпендикулярно до нього (див. рис.). Визначити період Т коливань такого маятника.
Розв’язання
| Дано: l = 1 м mстр = 3m1 d = 0,5 l mобр = m1 |
| Т ? |
Період коливань фізичного маятника визначають за формулою
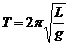 ,
,
 де g – прискорення вільного падіння, L – зведена довжина маятника.
де g – прискорення вільного падіння, L – зведена довжина маятника.
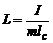 ,
,
m – маса маятника, lс – відстань від центра мас до осі коливань, I – момент інерції маятника відносно цієї осі. Вісь коливань на рисунку проходить через т. О перпендикулярно до площини рисунка. Тепер
 . (1)
. (1)
Момент інерції маятника рівний сумі моментів інерції стрижня І1 та обруча І2:
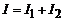 . (2)
. (2)
Момент інерції стрижня відносно осі, що проходить через його центр мас перпендикулярно до самого стрижня, визначається за формулою  , тому
, тому
 .
.
Момент інерції обруча знайдемо з використанням теореми Штейнера  , де: І – момент інерції відносно довільної осі, І0 – момент інерції відносно осі, що проходить через центр мас (в даному випадку обруча) паралельно до заданої осі; а – відстань між цими осями (див. рис.). Одержуємо для обруча
, де: І – момент інерції відносно довільної осі, І0 – момент інерції відносно осі, що проходить через центр мас (в даному випадку обруча) паралельно до заданої осі; а – відстань між цими осями (див. рис.). Одержуємо для обруча
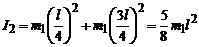 .
.
Підставляючи вирази І1 та І2 у формулу (2), знайдемо
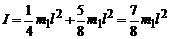 .
.
Відстань lс розраховуємо, виходячи з означення центра мас системи матеріальних точок (м.т.), точніше, з формули для обчислення координати центра мас
 , і – номер м.т.
, і – номер м.т.
( 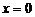 зручно вибрати в т. О, а саму вісь Ох направити до центра мас обруча; при цьому
зручно вибрати в т. О, а саму вісь Ох направити до центра мас обруча; при цьому 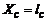 ). Маємо
). Маємо
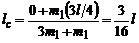 .
.
Підставляючи у формулу (1) вирази І, lс та масу маятника (4m1), знайдемо період його коливань:
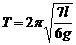 .
.
Числовий розрахунок:
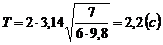 .
.
Відповідь: 2,2 с.
Приклад 5. Амплітуда згасаючих коливань за час t1 = 20 с зменшилася у два рази. У скільки разів вона зменшиться за час t2 = 1 хв?
Розв’язання
Дано:
t1 = 20 с
 t2 = 1 хв
t2 = 1 хв
|

|
Залежність амплітуди згасаючих коливань від часу визначається співвідношенням
 ,
,
де 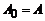 при
при 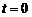 , b – коефіцієнт згасання. Запишемо згадане співвідношення для моментів часу t1 і t2:
, b – коефіцієнт згасання. Запишемо згадане співвідношення для моментів часу t1 і t2:
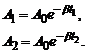
Перепишемо цю систему рівнянь у формі
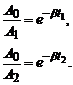
Очевидно, що 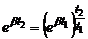 , тому відразу дістанемо робочу формулу
, тому відразу дістанемо робочу формулу
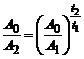 .
.
Виконаємо числовий розрахунок:
 ;
;
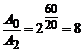 .
.
Відповідь: у вісім разів.
Приклад 6. Знайти жорсткість пружини ресори вагона, вага якого з вантажем Р = 5×105 Н, якщо при швидкості, модуль якої v = 12 м/с, вагон сильно розгойдується внаслідок поштовхів на стиках рейок. Довжина рейки l = 12,8 м. Вагон має 4 ресори.
Розв’язання
| Дано: Р = 5×105 Н v = 12 м/с l = 12,8 м n = 4 |
| k ? |
Значне розгойдування вагона виникає тоді, коли період власних коливань вагона з вантажем співпадає з періодом сили, котра викликає його вимушені коливання.
Період дії змушувальної сили знайдемо, розділивши довжину рейки на модуль швидкості вагона, тобто
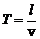 .
.
Період власних коливань вагона з вантажем (пружинного маятника) визначається за формулою
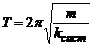 ,
,
m – маса системи,  – жорсткість системи з паралельно з’єднаних однакових пружин. Врахуємо, що потенціальна енергія такої системи стиснених пружин рівна n енергій однієї пружини, адже зміщення х у всіх пружин одне:
– жорсткість системи з паралельно з’єднаних однакових пружин. Врахуємо, що потенціальна енергія такої системи стиснених пружин рівна n енергій однієї пружини, адже зміщення х у всіх пружин одне:
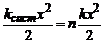 .
.
Тому 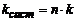 . Разом з тим,
. Разом з тим, 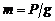 , g – прискорення вільного падіння.
, g – прискорення вільного падіння.
Прирівняємо праві частини двох формул для розрахунку періоду
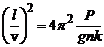 .
.
Звідси
 .
.
Числовий розрахунок:
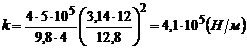 .
.
Відповідь: 0,41 МН/м.
Приклад 7. Плоска хвиля поширюється вздовж прямої зі швидкістю, модуль якої v = 20 м/с. Дві точки, що розміщені на цій прямій на відстанях х1 = 12 м та х2 = 15 м від джерела хвилі, коливаються з різницею фаз 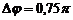 . Знайти довжину хвилі l, написати рівняння хвилі і знайти зміщення вказаних точок в момент часу
. Знайти довжину хвилі l, написати рівняння хвилі і знайти зміщення вказаних точок в момент часу 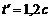 , якщо амплітуда коливань А = 0,1 м та початкова фаза хвилі
, якщо амплітуда коливань А = 0,1 м та початкова фаза хвилі 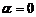 .
.
Розв’язання
Дано:
v = 20 м/с
х1 = 12 м
х2 = 15 м
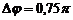
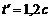 А = 0,1 м
А = 0,1 м
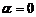
|
l ?
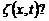

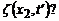
|
Рівняння плоскої хвилі, що поширюється вздовж осі Ох, має вигляд
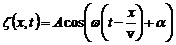 , (1)
, (1)
де: 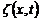 – зміщення в точці, що на відстані х від джерела, в момент часу t; w – циклічна частота коливань.
– зміщення в точці, що на відстані х від джерела, в момент часу t; w – циклічна частота коливань.
Фаза хвилі – аргумент косинуса, тому різниця фаз
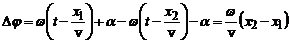 .
.
Оскільки  , а довжина хвилі
, а довжина хвилі 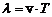 (Т – період коливань), то маємо
(Т – період коливань), то маємо
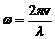 (2)
(2)
і  . Звідси
. Звідси
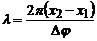 . (3)
. (3)
Рівняння хвилі (1) тепер запишемо з урахуванням формули (2):
 (4).
(4).
Підставимо у робочі формули (3) і (4) значення фізичних величин.
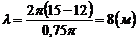 ,
,
 .
.
Тепер розрахуємо  та
та  :
:

Відповідь: 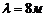 ;
;  ;
; 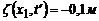 ;
; 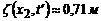 .
.
Приклад 8. В коливальному контурі, індуктивність якого L = 0,01 Гн, заряд конденсатора зменшується в десять разів за час, рівний періоду коливань Т = 1×10-5 с. Визначити опір контура.
Розв’язання
Дано:
L = 0,01 Гн
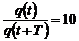 Т = 1×10-5 с
Т = 1×10-5 с
|
| R ? |
Рівняння згасаючих електромагнітних коливань має вигляд:
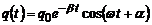 ,
,
де  – заряд у довільний момент часу t,
– заряд у довільний момент часу t, 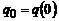 , b – коефіцієнт згасання, w – циклічна частота згасаючих коливань, a – початкова фаза.
, b – коефіцієнт згасання, w – циклічна частота згасаючих коливань, a – початкова фаза.
Через період коливань заряд стане рівним
 .
.
Оскільки 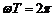 (зв’язок циклічної частоти з періодом), то
(зв’язок циклічної частоти з періодом), то  , тому маємо
, тому маємо
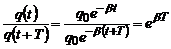
або
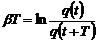 .
.
Коефіцієнт згасання для електромагнітних коливань
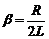 ,
,
тому попереднє співвідношення приймає вигляд
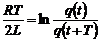
або
 .
.
Числовий розрахунок:
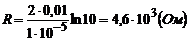 .
.
Відповідь: 4,6 кОм.
Приклад 9. Коливальний контур складається з конденсатора, ємність якого С = 1/3×10-8 Ф, та котушки з індуктивністю 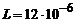 Гн. Знайти період вільних коливань у контурі, коефіцієнт згасання та логарифмічний декремент згасання, якщо опір котушки R = 60 Ом.
Гн. Знайти період вільних коливань у контурі, коефіцієнт згасання та логарифмічний декремент згасання, якщо опір котушки R = 60 Ом.
Розв’язання
| Дано: С = 1/3×10-8 Ф L = 12×10-6 Гн R = 60 Ом |
| T ? b ? l ? |
Період згасаючих електромагнітних коливань
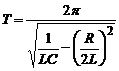 .
.
Коефіцієнт згасання
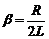 .
.
Логарифмічний декремент згасання
 .
.
Підставимо значення фізичних величин у виписані формули:
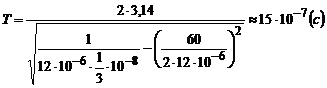 ;
;
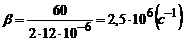 ;
;
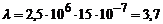 .
.
Відповідь: Т = 1,5 мкс; b = 2,5×106 с-1; l = 3,7.
Приклад 10. Плоска електромагнітна хвиля поширюється в однорідному ізотропному середовищі з діелектричною проникністю 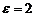 та магнітною проникністю
та магнітною проникністю 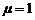 . Модуль амплітуди напруженості електричного поля хвилі
. Модуль амплітуди напруженості електричного поля хвилі 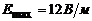 . Визначити: 1) фазову швидкість хвилі; 2) модуль амплітуди напруженості магнітного поля хвилі.
. Визначити: 1) фазову швидкість хвилі; 2) модуль амплітуди напруженості магнітного поля хвилі.
Розв’язання
Дано:

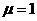
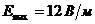
|
| v ? Hmax ? |
Фазова швидкість електромагнітних хвиль
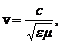
Модулі напруженостей електричного і магнітного полів хвилі Е та Н пов’язані співвідношенням

де 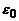 і
і  – електрична та магнітна сталі.
– електрична та магнітна сталі.
Оскільки рівняння плоскої хвилі (записане через модулі векторів  та
та  ) має вигляд
) має вигляд
 ,
,
де w – циклічна частота, t – час, k – хвильове число, x – відстань від джерела хвилі до точки простору, a – початкова фаза, то маємо аналогічний зв’язок між модулями амплітуд напруженостей:
 .
.
Звідси
 .
.
Числовий розрахунок:
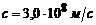 .
.
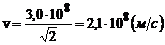 ;
; 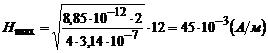 .
.
Відповідь: 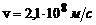 ;
;  .
.
Дата добавления: 2018-04-04; просмотров: 840; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
