Тема 4. Основные понятия теории пределов
Тема 1. Аналитическая геометрия на плоскости с элементами векторной алгебры.
Нормальным вектором  прямой
прямой  называется вектор, перпендикулярный каждому вектору, лежащему на данной прямой.
называется вектор, перпендикулярный каждому вектору, лежащему на данной прямой.
Если известны координаты нормального вектора  и известны координаты какой-либо точки
и известны координаты какой-либо точки  прямой
прямой  , то уравнение этой прямой можно записать в виде:
, то уравнение этой прямой можно записать в виде:
|
(1)
Прямая на плоскости может быть задана также своим общим уравнением:
|
(2)
Направляющим вектором  прямой
прямой  называется вектор, коллинеарный любому вектору данной прямой.
называется вектор, коллинеарный любому вектору данной прямой.
Если известны координаты направляющего вектора  и известны координаты какой-либо точки
и известны координаты какой-либо точки  прямой
прямой  , то уравнение этой прямой можно записать в виде:
, то уравнение этой прямой можно записать в виде:
|
(3)
Если известны координаты двух точек  и
и  прямой
прямой  , то уравнение этой прямой имеет вид:
, то уравнение этой прямой имеет вид:
|
(4)
Расстояние от точки  , не лежащей на прямой
, не лежащей на прямой  , до этой прямой можно найти по формуле:
, до этой прямой можно найти по формуле:
|
|
|
|
(5)
где  - коэффициенты общего уравнения (2).
- коэффициенты общего уравнения (2).
Тема 2.Аналитическая геометрия в пространстве.
Нормальным вектором  плоскости
плоскости  называется вектор, перпендикулярный каждому вектору, лежащему в данной плоскости.
называется вектор, перпендикулярный каждому вектору, лежащему в данной плоскости.
Если известны координаты нормального вектора  и известны координаты какой-либо точки
и известны координаты какой-либо точки  плоскости
плоскости  , то уравнение этой плоскости можно записать в виде:
, то уравнение этой плоскости можно записать в виде:
|
(6)
Плоскость в пространстве может быть задана также своим общим уравнением:
|
(7)
Расстояние от точки  , не лежащей на плоскости
, не лежащей на плоскости  , до этой плоскости можно найти по формуле:
, до этой плоскости можно найти по формуле:
|
, (8)
где  - коэффициенты общего уравнения (11).
- коэффициенты общего уравнения (11).
Рассмотрим в пространстве некоторую прямую  , проходящую через точку
, проходящую через точку 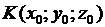 и имеющую направляющий вектор
и имеющую направляющий вектор  . Уравнение этой прямой имеет вид:
. Уравнение этой прямой имеет вид:
|
(9)
|
|
|
Если известны координаты двух точек  и
и  прямой
прямой  , то уравнение этой прямой можно записать в виде:
, то уравнение этой прямой можно записать в виде:
|
(10)
Угол между плоскостью, заданной общим уравнением (11), и прямой, заданной каноническими уравнениями (13), можно найти по формуле:
|
(11)
где  - направляющий вектор прямой,
- направляющий вектор прямой,  - нормальный вектор плоскости.
- нормальный вектор плоскости.
Тема 3. Элементы линейной алгебры.
Матрицей  называется прямоугольная таблица чисел, состоящая из
называется прямоугольная таблица чисел, состоящая из  строк и
строк и  столбцов.
столбцов.  - элемент матрицы; i –номер строки, j – номер столбца, на пересечении которых находится данный элемент. Если число строк совпадает с числом столбцов
- элемент матрицы; i –номер строки, j – номер столбца, на пересечении которых находится данный элемент. Если число строк совпадает с числом столбцов  , то матрица является квадратной.
, то матрица является квадратной.
Определителем 2-го порядка, соответствующим квадратной матрице  , называется число, определяемое равенством:
, называется число, определяемое равенством:
|
(12)
Определителем 3-го порядка, соответствующим квадратной матрице  , называется число, определяемое равенством:
, называется число, определяемое равенством:
|
(13)
Символически вычисление определителя 3-го порядка можно изобразить схемой:
|
|
|

т.е. с неизменным знаком берутся произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали; с противоположным знаком берутся произведения элементов, стоящих на второстепенной диагонали и в вершинах треугольников с основаниями, параллельными второстепенной диагонали.
Системой трёх линейных уравнений с тремя неизвестными называется система вида

где  - числовые коэффициенты при неизвестных
- числовые коэффициенты при неизвестных  , образующие основную матрицу системы. Если определитель
, образующие основную матрицу системы. Если определитель  , соответствующий основной матрице, отличен от нуля (т.е. система невырожденная), то единственно существующее решение
, соответствующий основной матрице, отличен от нуля (т.е. система невырожденная), то единственно существующее решение  такой системы можно найти по формулам Крамера:
такой системы можно найти по формулам Крамера:
|
(14)
|
(15)
т.е. столбец коэффициентов при соответствующем неизвестном в главном определителе заменяется столбцом свободных членов, после чего определитель  вычисляется по правилу треугольников (см. выше).
вычисляется по правилу треугольников (см. выше).
Тема 4. Основные понятия теории пределов.

| Число  называется пределом функции называется пределом функции  при значениях аргумента при значениях аргумента  , стремящихся к значению , стремящихся к значению  (обозначается (обозначается  ), если как бы малó ни было положительное число ), если как бы малó ни было положительное число  , всегда найдётся такое положительное число , всегда найдётся такое положительное число  (зависящее от (зависящее от  ), что для всех ), что для всех  , удовлетворяющих неравенству , удовлетворяющих неравенству  , выполняется и неравенство , выполняется и неравенство  (то есть (то есть
|
для всех значений аргумента  , попадающих в интервал радиуса
, попадающих в интервал радиуса  с центром в точке
с центром в точке  , разница между значениями функции и её пределом
, разница между значениями функции и её пределом  становится сколь угодно малой).
становится сколь угодно малой).
Число  называется пределом функции
называется пределом функции  при
при  (обозначается
(обозначается 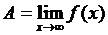 ), если как бы малó ни было положительное число
), если как бы малó ни было положительное число  , всегда найдётся такое положительное число
, всегда найдётся такое положительное число  (зависящее от
(зависящее от  ), что для всех
), что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется и неравенство
, выполняется и неравенство  (то есть для всех значений аргумента
(то есть для всех значений аргумента  , попадающих в интервалы
, попадающих в интервалы  или (
или (  ), разница между значениями функции и её пределом
), разница между значениями функции и её пределом  становится сколь угодно малой).
становится сколь угодно малой).
Отметим некоторые свойства предела функции:
1) Предел суммы (разности) двух функций равен сумме (разности) пределов слагаемых:
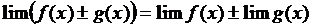
2) Предел произведения двух функций равен произведению пределов сомножителей:

3) Предел постоянной величины равен самой постоянной:

4) Постоянный множитель можно выносить за знак предела:

5) Предел дроби равен отношению предела числителя к пределу знаменателя (если предел знаменателя отличен от нуля):
 , при
, при 
Функция  называется бесконечно большой при
называется бесконечно большой при  (
(  ), если
), если  (
(  ).
).
Функция  называется бесконечно малой при
называется бесконечно малой при  (
(  ), если
), если  (
(  ).
).
Бесконечно малые и бесконечно большие функции связаны друг с другом следующим образом: если  - бесконечно большая, то
- бесконечно большая, то  - бесконечно малая. И наоборот: если
- бесконечно малая. И наоборот: если  - бесконечно малая, то
- бесконечно малая, то  - бесконечно большая.
- бесконечно большая.
Если при отыскании предела рациональной дроби пределы числителя и знаменателя равны нулю (или бесконечны), то такие ситуации называют неопределённостями и символически обозначают  (или
(или  ). Существуют и другие виды неопределённостей, например:
). Существуют и другие виды неопределённостей, например:  ,
,  ,
, 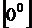 ,
,  . Для каждого вида неопределённости существует свой метод её устранения.
. Для каждого вида неопределённости существует свой метод её устранения.
Правило1: Для устранения неопределённости  при
при  , возникшей в пределе рациональной дроби, нужно в числителе и знаменателе выделить линейный множитель
, возникшей в пределе рациональной дроби, нужно в числителе и знаменателе выделить линейный множитель 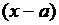 , дающий эту неопределённость, и сократить дробь.
, дающий эту неопределённость, и сократить дробь.
Правило 2: Для устранения неопределённости  при
при  , возникшей в пределе рациональной дроби, нужно числитель и знаменатель разделить на наивысшую степень
, возникшей в пределе рациональной дроби, нужно числитель и знаменатель разделить на наивысшую степень  , присутствующую в этой дроби.
, присутствующую в этой дроби.
Число  называется пределом функции
называется пределом функции  слева в точке
слева в точке  , если как бы малό ни было положительное число
, если как бы малό ни было положительное число  , всегда можно указать такое положительное число
, всегда можно указать такое положительное число  (зависящее от
(зависящее от  ), что для всех
), что для всех  из интервала
из интервала  выполняется неравенство
выполняется неравенство  . Предел слева (левый предел) обозначается:
. Предел слева (левый предел) обозначается:

Аналогично определяется предел функции справа  .
.
Левый и правый пределы функции называются односторонними пределами.
Функция  называется непрерывной в точке
называется непрерывной в точке  ,если:
,если:
1) она определена в этой точке;
2) 
Если нарушается хотя бы одно из условий непрерывности, то говорят, что функция  терпит разрыв в точке а (или является разрывной).
терпит разрыв в точке а (или является разрывной).
Точки разрыва функции можно классифицировать следующим образом:
- если оба односторонних предела в точке а существуют и конечны (равные друг другу или различные), то точка а является точкой разрыва первого рода;
- если хотя бы один из односторонних пределов в точке а не существует или бесконечен, то точка а является точкой разрыва второго рода.
|
|

Поскольку определение вертикальной асимптоты  совпадает с определением точки разрыва второго рода (см. выше), то можно утверждать, что вертикальные асимптоты проходят через точки разрыва второго рода.
совпадает с определением точки разрыва второго рода (см. выше), то можно утверждать, что вертикальные асимптоты проходят через точки разрыва второго рода.
|

 является прямая
является прямая 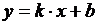 , где
, где
(16)
|
(17)
но только в том случае, если оба этих предела существуют и конечны.
В частности, при  наклонная асимптота становится горизонтальной асимптотой
наклонная асимптота становится горизонтальной асимптотой  .
.
Дата добавления: 2018-04-05; просмотров: 219; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!









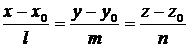








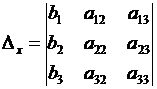 ,
,  ,
, 
 (или
(или  , или
, или  ).
).

