Метатеоретические свойства исчисления предикатов со схемами аксиом

1. Рассмотренные аксиоматическое и натуральное исчисления предикатов являются дедуктивно эквивалентными по классу выводимостей, т. е. в системеисчисления предикатов со схемами аксиом из посылок Г выводима формула B, если и только если эта же выводимость имеет место и в натуральном исчислении предикатов первого порядка. Правилу modus ponens аксиоматического исчисления предикатовсоответствует правило исключения импликации, а правилу генерализации – правило введения квантора общности. Также все схемы аксиом, доказуемые в системе исчисления предикатов со схемами аксиом, доказуемы и в системе натурального исчисления.

2. Исчисление предикатов со схемами аксиом непротиворечиво относительно исчисления высказываний со схемами аксиом.

Введем функцию . Тогда выражение  будет обозначать формулу исчисления высказываний со схемами аксиом, образованную из формулы A исчисления предикатовследующим образом:

– в формуле A устраняются все кванторы существования (по определению ;

– необходимо опустить все кванторы общности и термы;

– предикаторы замещают пропозициональными переменными таким образом, что одинаковые предикаторы замещаются одинаковыми пропозициональными переменными.

В этом случае для функции  будут выполняться свойства:

– ;

– ;

– ;

– .

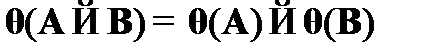Для обоснования метаутверждения о непротиворечивости аксиоматического исчисления предикатов относительно аксиоматического исчисления высказываний необходимо доказать лемму о том, что, будучи применена к произвольной теореме исчисления предикатовсо схемами аксиом, функция  порождает тождественно-истинную формулу логики высказываний.

Применив эту лемму к аксиомам CA1-CA10, функция  породит некоторую формулу этой же самой структуры, т. е. породит аксиому исчисления высказываний со схемами аксиом. Что касается кванторной части, то любой частный случай CA11, т. е. 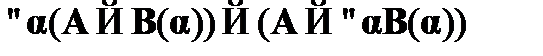, будет преобразован функцией в формулу вида 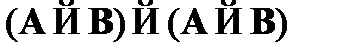. Все частные случаи этой схемы являются тождественно-истинными формулами. То же самое касается аксиомы CA12.Любой частный случай CA13-14
будет преобразован в формулу вида , частные случаи которой являются тождественно-истинными.

Итак, если формула A исчисления предикатов со схемами аксиом – теорема, то  – тождественно-истинная формула логики высказываний. Таким образом, лемма доказана.

Доказательство метатеоремы

Доказательство будет вестись методом от противного. Допустим, что исчисление предикатов со схемами аксиом (CA_Pr) синтаксически противоречиво:

(1) 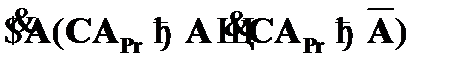      – допущение;

(2) 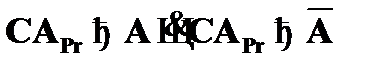             – исключение  к (1), A– абс. огр.;

(3) 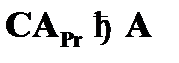                                 – исключение  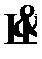к (2);

(4) 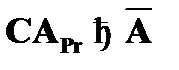                                 – исключение  к (2);

(5)                                     – тождественно-истинная формула по лемме;

(6)                                     – тождественно-истинная формула по лемме;

(7) 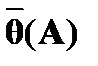                                    – из (6) по ;

(8)       – введение отрицания на основании (5) и (7).

Метатеорема доказана.

3. Исчисление предикатов со схемами аксиом семантически непротиворечиво.

В доказательстве данной метатеоремы необходимо показать общезначимость всех схем аксиом и правил вывода. В отношении правил вывода это означает необходимость показать, что они позволяют получать из общезначимых формул только общезначимые формулы. Допустим, что некоторая формула, совпадающая со схемой аксиомы CA1,
не является общезначимой, т. е. :

(1) 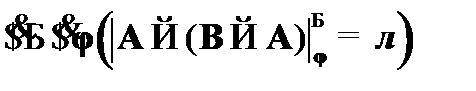      – допущение о необщезначимости CA1;

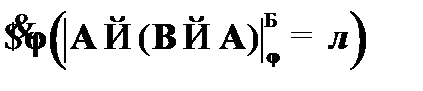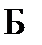(2)            –  к (1),  – абс. огр.;

(3) 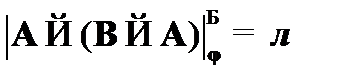                          –  к (2),  – абс. огр.;

(4)                               – по определению из (3);

(5) 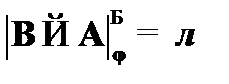                            – по определению из (3);

(6)                                 – по определению из (5);

(7) 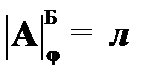                                   – по определению из (5);

(8) 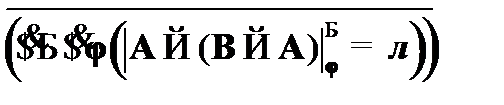   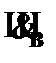– ,к (4) и (7);

(9)       – закон де Моргана к (8);

(10) 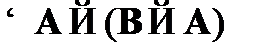                       – по определению общезначимости из (9).

Аналогичным образом показывается общезначимость остальных схем аксиом.
Остаются кванторные формулы CA11 и CA13(доказательство CA12 и CA14производится аналогичным образом), а также инвариантность правил modus ponens и генерализации. Как и в предыдущем случае, доказательство будет вестись методом от противного:

(1)  – допущение, где A не содержит свободно ;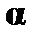

(2)  –  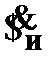к (1),  – абс. огр.;

(3)         –  к (1),  – абс. огр.;

(4) 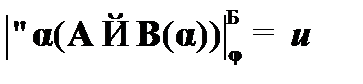                          – по определению из (3);

(5)                                        – по определению из (3);

(6) 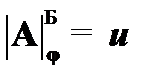                                             – по определению из (5);

(7)                                     – по определению из (5);

(8)                                 – по определению из (7), где  отличается от  не более чем значением переменной ;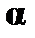

(9)                                         –  к (8), – абс. огр.;

(10)                      – по определению к (4);

(11)                               –  к (10);

(12)                        – по определению из (11);

(13)                                            – допущение;

Примечание. Индивидная переменная α не входит свободно в формулу A, а на всех остальных свободных переменных имеет место равенство функций, т. е. .

(14) 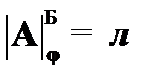                                           – из (13) в силу равенства ;

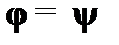(15) 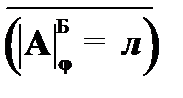                                        – , к (6), (14);

(16) 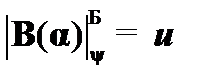                                       – , к (12), (15);

(17) 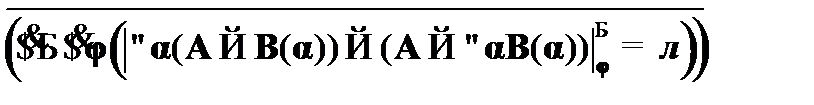 – , к (9), (16);

(18) 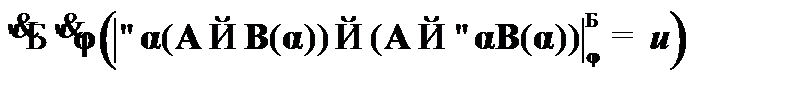– закон де Моргана к (17);

(19) 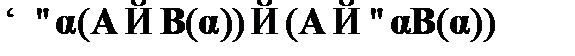                 – из (18).

Доказательство общезначимости CA13

(1) 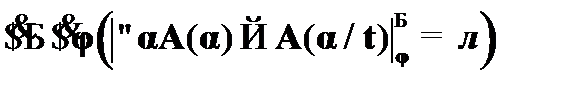– допущение о необщезначимости CA13;

(2) 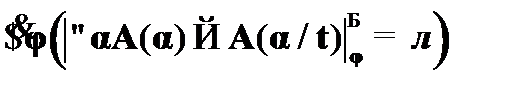   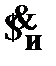   –  к (1),  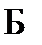– абс. огр.;

(3)          –  к (1),  – абс. огр.;

(4) 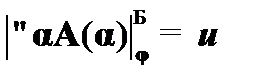                          – по определению из (3);

(5)                       – по определению из (3);

(6) 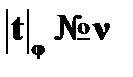                                  – из (4), т. е. объект  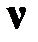не выполняет условия A;

(7)                   – по определению из (4);

(8)                               –  к (10);

(9) 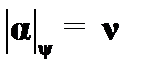                                 – из (8) по определению;

(10)                                 – из (9), т. е. объект 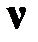 выполняет условие A;

(11)  – , к (6), (10);

(12) 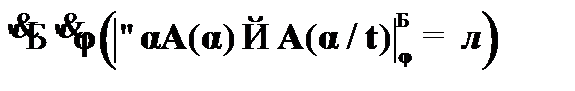– закон де Моргана к (11);

(13)           – по определению общезначимости из (12).

Таким образом, доказана общезначимость всех аксиом. Для правила вывода modus ponens это было уже доказано. Осталось правило генерализации. Согласно данному правилу если , то .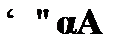

Доказательство

(1) 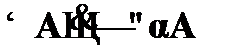                        – допущение;

(2) 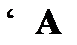                                       –  из (1);

(3) 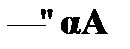   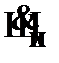                               –  из (1);

(4)                    – определение общезначимости к (2);

(5) 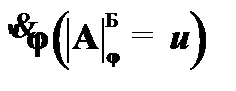                       –  к (4);

(6)                                –  к (5);

(7) 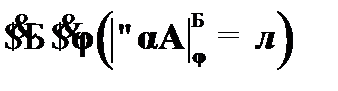                              – определение общезначимости к (3);

(8) 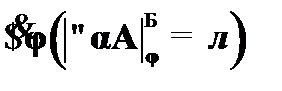   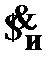                –  к (1),  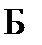– абс. огр.;

(9)                               –  к (1),  – абс. огр.;

(10)                      – по определению из (9);

(11)    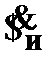                          –  к (10),  – абс. огр.;

(12)    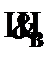                          – , к (6), (11);

(13) 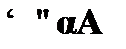                                – , к (12).

Таким образом, показано, что все схемы аксиом являются схемами общезначимых формул исчисления предикатов. Правила вывода также сохраняют свойство формул. Следовательно, любая доказуемая в исчислении предикатов со схемами аксиом формула является общезначимой.

4. Исчисление предикатов со схемами аксиом является синтаксически непротиворечивым и семантически полным. Синтаксис и семантика данного исчисления адекватны друг другу.

5. Исчисление предикатов со схемами аксиом неразрешимо, а также не является максимальным. Последнее означает, что к данной системе без противоречия можно присоединять в качестве новых схем аксиом недоказуемые в ней выражения. Это приводит к сужению класса возможных реализаций языка, что позволяет строить нелогические теории.

---

Дата добавления: 2018-04-05; просмотров: 441; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!