Натуральное исчисление предикатов

⇐ ПредыдущаяСтр 21 из 25Следующая ⇒

В натуральном исчислении предикатов сохраняются те же правила, что использовались нами при построении натурального исчисления высказываний, но к ним добавляются кванторные правила.

Кванторные правила вывода

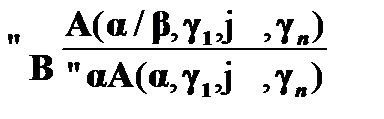– правило введения квантора общности (β – абсолютно ограничено, а 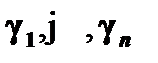– ограничения);

– правило исключения квантора общности;

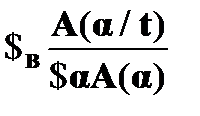– правило введения квантора существования;

– правило введения квантора общности ( – абсолютно ограничено, а – ограничения).

Как видно из приведенных правил, их применение требует выполнения ряда условий. Во-первых, выражение является результатом правильной подстановки
в формулу вместо всех свободных вхождений переменной терма t. Выражение – метаязыковая запись результата правильной подстановки в выражение вместо всех свободных вхождений переменной индивидной переменной .
Подстановка является правильной в том случае, если число вхожденийлюбой связанной переменной, определенное для формулы , остается неизменным и после подстановки.

Во-вторых, как мы уже знаем, свободные индивидные переменные трактуются как пробегающие по некоторому универсуму рассуждения U и принимающие любые значения на нем. Но в составе формул индивидные переменные не всегда являются знаками, обозначающими произвольный объект универсума. Свободная индивидная переменная употреблена в некоторой формуле в интерпретации всеобщности, если она в составе формулы понимается как знак, обозначающий произвольный объект из универсума.
Если выведение истинного предложения из некоторой высказывательной формы необходимо ограничить возможными значениями индивидных переменных, то говорят, что переменная использована в условной интерпретации. В случае условной интерпретации переменных выбор значений для одной переменной (абсолютное ограничение – абс. огр.) ограничивает выбор значений для других свободных переменных, входящих в это выражение (ограничение – огр.).

Правило исключения квантора общности ( ) разрешает осуществить переход от формулы вида к формуле . При этом устраняется квантор общности, а в формуле 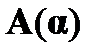необходимо осуществить подстановку терма t вместо всех свободных вхождений переменной .

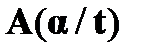Правило введения квантора существования ( ) позволяет осуществить переход от формулы к формуле . При этом посылка должна быть результатом правильной подстановки вместо всех свободных вхождений переменной терма t в формулу .

Правило исключения квантора существования ( ) разрешает осуществить переход от формулы 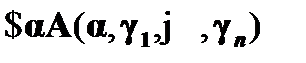к формуле . В посылке правила утверждается наличие в универсуме объекта, удовлетворяющего условию , что, в свою очередь, позволяет считать таковым объект, обозначенный свободной переменной . Иными словами, необходимо осуществить выбор такого значения для , что утверждение будет истинно. Переменная абсолютно ограничена, и ее следует рассматривать как такое имя объекта, которое удовлетворяет условию 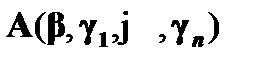. Выбор значения для 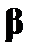ограничивает возможные значения для остальных свободных индивидных переменных 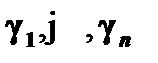. Таким образом,
в данном правиле переменные – это все те свободные индивидные переменные, которые входят в выражение .

Правило введения квантора общности ( 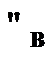) позволяет перейти от формулы к формуле . Однако в данном случае мы имеем две возможности. Во-первых, переменная при данных фиксированных значениях входит в формулу в интерпретации всеобщности. В таком случае переход от к формуле является вполне допустимым. Во-вторых, формула может принимать значение «ложь» при каких-то фиксированных значениях и при некоторых значениях . Тогда следует выбрать одно из таких значений для переменной . Это сделает переменную 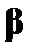абсолютно ограниченной, а все остальные свободные переменные ограниченными. Формула является при таком выборе ложной. Но, как нам известно, из ложного высказывания следует все, что угодно, а значит, будет следовать и выражение . В данном правиле переменные 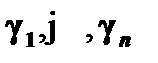– это все свободные переменные формулы .

Применение кванторных правил позволяет как менять подкванторные индивидные переменные на новые переменные, так и обходиться без их замены.

Выводом в натуральном исчислении предикатов первого порядка называется
непустая конечная последовательность формул , которая должна удовлетворять условиям:

– каждая является посылкой либо получена из предыдущих формул по одному из правил вывода;

– в случае если применялись правила введения импликации или введения отрицания, то исключаются из дальнейших шагов построения вывода все формулы, начиная с последней посылки и вплоть до результата применения данного правила;

– ни одна индивидная переменная не может быть абсолютно ограничена дважды;

– ни одна переменная не может ограничивать сама себя;

– только наличие завершенного вывода гарантирует, что между посылками и заключением имеется отношение логического следования.

Доказательством называется вывод из пустого множества посылок. Последняя формула в доказательстве называется доказуемой формулой или теоремой.

Завершенным называется вывод, в котором никакая переменная абсолютно не
ограничивается в выводе, не встречается свободно ни в исключенных посылках, ни в заключении. Завершенным доказательством называется завершенный вывод из пустого множества посылок.

Говоря о правилах (эвристиках) выбора посылок в натуральном исчислении предикатов, следует помнить об эвристиках, сформулированных в отношении натурального исчисления высказываний. К ним добавляется еще одна, касающаяся квантифицированных формул.

Четвертая эвристика. Если в результате применения первой эвристики удалось дойти до формулы, имеющей вид или , то можно далее продолжить выбор посылок из формулы A по первой или второй эвристикам, не обращая внимания на наличие кванторов.

Пример 6. Обоснуем выводимость вида :

(1) – посылка;

(2) 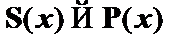– 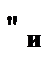к (1);

(3) 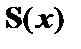– посылка;

(4) 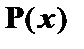– modus ponens к (2), (3);

(5) – к (3), (4);

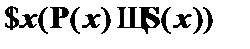(6) – к (5).

Все условия вывода в данном случае соблюдены, вывод является завершенным.

Пример 7. Докажем выводимость вида :

(1) – посылка;

(2) – к (1), x – абс. огр.;

(3) – 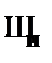к (2);

(4) – к (2);

(5) – к (3), (4).

На последнем шаге вывод должен быть прерван, так как применить правило введения квантора существования нельзя. Это привело бы к повторному ограничению переменной x.

Пример 8. Докажем теорему :

(1) – посылка по 1-й эвристике;

(2) – посылка по 1-й эвристике;

(3) – к (1);

(4) – к (1);

(5) – к (4);

(6) – modus ponens к (5), (2);

(7) – к (3);

(8) – modus ponens к (7), (6);

(9) – 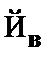к (2), (8);

(10) 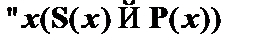– к (9), x – абс. огр;

(11) – к (1), (10).

Данный вывод является завершенным доказательством. Причем на шаге (2) доказательства применялась четвертая эвристика к формуле .

В целом для натурального исчисления предикатов справедливым является метаутверждение: завершенный вывод 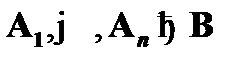имеет место тогда и только тогда, когда . Это говорит об адекватной формализации логики предикатов первого порядка в натуральном исчислении предикатов.

Дата добавления: 2018-04-05; просмотров: 442; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 16 17 18 19 202122 23 24 25 Следующая ⇒

Мы поможем в написании ваших работ!