Основные логические отношения
Наряду с выделением логических законов в рамках пропозициональной логики решается задача по установлению логических отношений (отношения по истинности и ложности) между формулами. При этом учитываются возможные совместные значения формул при различных интерпретациях нелогических символов в их составе.
Данные определения задают логические отношения не только между формулами логики высказываний, но и между формулами любой другой логической теории. Фундаментальными являются отношения совместимости по истинности, совместимости по ложности и логического следования. Производными от них являются отношения контрадикторности, контрарности, субконтрарности, эквивалентности, подчинения и независимости.
Формулы множестваГназываются совместимыми по истинности в некоторой логической теорииТ, если и только если вТсуществует интерпретация нелогических символов, входящих в указанные формулы, при которой каждая формула, входящая вГ, принимает значение «истина».Если данное условие не соблюдается, то рассматриваемые формулы являются несовместимыми по истине.
Формулы множестваГназываются совместимыми по ложности в теорииТ, если и только если вТсуществует интерпретация нелогических символов, входящих в указанные формулы, при которой каждая формула из Гпринимает значение «ложь». В противном случае формулы несовместимы по ложности.
Из множества формулГлогически следует формулаВ в некоторой логической теории Т, если и только если вТне существует интерпретации нелогических символов, входящих вГиВ, при которой каждая формула из Гпринимает значение «истина»,
а формулаВ– значение «ложь». В противном случае говорят, что формула B не следует из Г. Выражение «из множества формул Г логически следует B» может быть записано так: «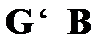 
», где знак « 
» указывает на отношение логического следования.
|
|
|
ФормулыAиBнаходятся в отношении контрадикторности (противоречия), если и только если они несовместимы по истинности и несовместимы по ложности.
ФормулыAиBнаходятся в отношении контрарности (противоположности), если и только если они несовместимы по истинности, но совместимы по ложности.
ФормулыAиBнаходятся в отношении субконтрарности (подпротивоположности), если и только если они совместимы по истинности, но несовместимы по ложности.
Формулы AиBлогически эквивалентны, если и только если изAлогически следуетB, а из Bлогически следуетA.
ФормулаАлогически подчиняется формулеB, если и только если при логическом следовании AизB ( 
)нет обратного логического следования( 
).
ФормулыAиBлогически независимы, если они совместимы по истинности
и ложности и при этом не следуют друг из друга.
|
|
|
| Таблица 7 | ||||||
| p | q | 
| 
| 
| 
| |
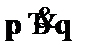
| 1 | и | и | и | и | и | л |
| 2 | и | л | л | л | л | и |
| 3 | л | и | и | л | л | и |
| 4 | л | л | и | и | л | л |
Рассмотренные выше таблицы истинности позволяют однозначно решить вопрос об отношениях между формулами пропозициональной логики. К примеру, рассмотрим отношения между формулами 
, 
, 
и 
. Для этого нам необходимо построить совместную для данных формул таблицу истинности (табл. 7).
Как видно из приведенной таблицы, формулы 
и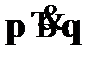 
являются контрадикторными, так как во всех строках при истинности одной из них вторая обязательно оказывается ложной. Из формулы 
логически следует формула 
(при истинности первой, вторая ни в одной строке не является ложной), но обратного следования нет (так как в третьей строке, при истинности импликации, эквиваленция ложна). Это значит, что данные формулы находятся в логическом подчинении. Точно в таком же отношении находятся и формулы 
и 
. Кроме того, можно утверждать, что из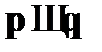 
логически следует формула 
. Следовательно, далее можно установить любые отношения между формулами.
В пропозициональной логике истинными являются несколько утверждений метатеоретического характера. Наиболее важными из них являются:
|
|
|
1. Из некоторой формулы Aлогически следует формула B тогда и только тогда, когда формула ( 
) является тождественно-истинной, т. е.
.
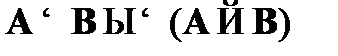Данное свойство может быть формально обобщено:
,
т. е. из посылок 
логически следует формула B, если и только если формула 
является тождественно-истинной. Данное метаутверждение следует из самого смысла логического следования и импликации.
2. Если тождественно-истинной является формула A и тождественно-истинной является формула 
, то тождественно-истинной является и формула B. Формализовано это утверждение может быть посредством записи:
.
Данное утверждение, в сущности, раскрывает правило modus ponens:
.
3. Если вместо любой пропозициональной переменной везде, где она встречается в тождественно-истинной формуле, подставить произвольную формулу, то в результате мы снова получим тождественно-истинную формулу.
Дата добавления: 2018-04-05; просмотров: 594; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!