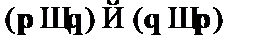Таблицы истинности. Виды формул
После того как задан алфавит пропозициональной логики, можно перейти к следующему шагу, т. е. заняться собственно построением логической теории. При этом для построения пропозициональной логики используется метод таблиц истинности.
Прежде всего следует решить комплекс вопросов, связанных с интерпретацией пропозициональных переменных.Для этого следует, во-первых, из множества формул выделить класс формул, являющихся законами, и, во-вторых, установить логические отношения между формулами.
С этой целью необходимо установить, каким образом могут интерпретироваться пропозициональные переменные в формуле. Процедура интерпретации нелогических символов состоит в приписывании им значений. Тип значений каждого такого символа должен быть тем же самым, что и у соответствующих значений естественного языка.
Значениями пропозициональных переменных являются абстрактные объекты – «истина» и «ложь». Допустимой интерпретацией переменных  является произвольный набор их значений, т. е. любая последовательность
является произвольный набор их значений, т. е. любая последовательность 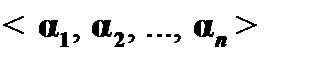 , где каждое
, где каждое 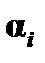 есть либо «истина», либо «ложь», причем
есть либо «истина», либо «ложь», причем  есть значение переменной
есть значение переменной  . Если эта последовательность содержит две переменные, то наборами значений являются упорядоченные пары: <и, и>, <и, л>, <л, и>, <л, л>.
. Если эта последовательность содержит две переменные, то наборами значений являются упорядоченные пары: <и, и>, <и, л>, <л, и>, <л, л>.
Число всех возможных наборов значений n переменных равно 2n. Чтобы получить все слова длины n автоматически, одной из переменных приписывают 2n раз значение и и л, меняя их через 1. Следующей переменной приписывают эти же значения, меняя их через 2, третьей – меняя через 4 и т. д., пока не будут приписаны значения всем n переменным.
|
|
|
Табличные представления пропозициональных связок. Следующий этап построения логической теории состоит в придании точных значений символам алфавита. Исходными логическими символами являются пропозициональные связки, которые можно рассматривать как знаки функций истинности – функций, аргументами и значениями которых являются «истина» и «ложь».
Придать значение пропозициональной связке (в пропозициональной логике) – значит сопоставить ей определенную функцию истинности. Удобнее всего задать эти функции табличным способом. Так как данные операции могут применятся не только к пропозициональным связкам, но и к произвольным формулам, мы таблично зададим указанные связки именно для этого случая.
| Таблица 1 | ||||||
| А | В | 
| 
| 
| 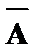
| 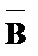
|
| и | и | и | и | и | л | л |
| и | л | л | и | л | л | и |
| л | и | л | и | и | и | л |
| л | л | л | л | и | и | и |
В первых двух столбцах табл. 1указаны все возможные наборы значений формул А и В, а в остальных – значения, которые принимают формулы 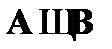 ,
, ,
,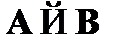 ,
,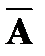 и
и  в соответствующих случаях. Данную таблицу можно рассматривать как определение функции истинности, представленной знаками ˄, ˅, É
в соответствующих случаях. Данную таблицу можно рассматривать как определение функции истинности, представленной знаками ˄, ˅, É
и знаком отрицания. Знаки ˄, ˅ и É являются бинарными связками, а знак внешнего отрицания – унарной связкой. Бинарные связки позволяют издвух формул образовать новую, более сложную формулу.
|
|
|
Данная таблица определяет функцию истинности конъюнкции (˄) следующим образом:  , в остальных случаях функция принимает значение л, т. е. в конъюнктивных высказываниях утверждается одновременное наличие двух положений дел – описываемого в А и описываемого в В. Если оба положения имеют место в действительности, то конъюнктивное высказывание является истинным. В предложениях естественного языка в роли знака конъюнкции выступают союзы «и», «а», «но» и иные тождественные с ними по значению. Однако не любое употребление союза «и» в естественном языке выражает указанный смысл связки ˄. Во многих случаях союз «и» выражает некоторую последовательность действий: «Я вышел из дома и закрыл за собой дверь».
, в остальных случаях функция принимает значение л, т. е. в конъюнктивных высказываниях утверждается одновременное наличие двух положений дел – описываемого в А и описываемого в В. Если оба положения имеют место в действительности, то конъюнктивное высказывание является истинным. В предложениях естественного языка в роли знака конъюнкции выступают союзы «и», «а», «но» и иные тождественные с ними по значению. Однако не любое употребление союза «и» в естественном языке выражает указанный смысл связки ˄. Во многих случаях союз «и» выражает некоторую последовательность действий: «Я вышел из дома и закрыл за собой дверь».
Поэтому при выявлении логической формы данного высказывания нельзя заменить союз «и» знаком «&».
Высказывания, содержащие дизъюнкцию (˅), выражают мысль о наличии, по крайней мере, одного из двух положений дел. При этом, в случае нестрогого характера разделения, не исключено их одновременное наличие. Таким образом, при рассмотрении дизъюнкции как функции получаем:  , т. е. при одновременной ложности аргументов данная функция принимает значение л, во всех прочих случаях ее значение равно и. В естественном языке дизъюнкция выражается посредством связок «или», «либо ..., либо ...» и иных, эквивалентных им. Следует помнить, что данные связки могут указывать на альтернативность ситуаций. В этом случае мы имеем дело со строгой дизъюнкцией(
, т. е. при одновременной ложности аргументов данная функция принимает значение л, во всех прочих случаях ее значение равно и. В естественном языке дизъюнкция выражается посредством связок «или», «либо ..., либо ...» и иных, эквивалентных им. Следует помнить, что данные связки могут указывать на альтернативность ситуаций. В этом случае мы имеем дело со строгой дизъюнкцией(  ), для которой, помимо указанного условия, должно также выполняться еще одно условие ложности:
), для которой, помимо указанного условия, должно также выполняться еще одно условие ложности:  . Пример строгой дизъюнкции: «У Иванова либо есть алиби, либо его нет».
. Пример строгой дизъюнкции: «У Иванова либо есть алиби, либо его нет».
|
|
|
Материальная импликация (É) описывает условную связь. Выражение, стоящее слева от знака импликации, именуется антецендентом (основанием),справа – консеквентом (следствием). Импликация предполагает, что при наличии положения дел, описываемого антецендентом (А), имеет место также и положение дел, описываемое консеквентом (В). Отсюда следует, что при истинности основания следствие не может быть ложным. В функциональной форме записи условие ложности импликации может быть записано так: 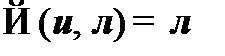 . Во всех остальных случаях импликативное (условное) высказывание принимает значение и. Наиболее адекватным выражением материальной импликации в естественном языке является использование конструкции «если …, то …». Однако во многих случаях этот союз несет и дополнительную нагрузку – выражает связь между положениями дел, при которой одно из них обусловливает другое.
. Во всех остальных случаях импликативное (условное) высказывание принимает значение и. Наиболее адекватным выражением материальной импликации в естественном языке является использование конструкции «если …, то …». Однако во многих случаях этот союз несет и дополнительную нагрузку – выражает связь между положениями дел, при которой одно из них обусловливает другое.
|
|
|
| Таблица 2 | ||
| – | 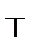
| 
|
| < > | и | л |
В табл. 1 указаны всего лишь четыре булевы функции, соответствующие исходным пропозициональным связкам. В общем же случае число булевых функций бесконечно, хотя для каждого n число
n-местных истинностно-истинностных функций конечно и равно  . Например, количество одноместных функций составляет 4, двухместных – 16, трехместных – 256 и т. д. Таким образом, существуют только две нульместные булевы функции вида
. Например, количество одноместных функций составляет 4, двухместных – 16, трехместных – 256 и т. д. Таким образом, существуют только две нульместные булевы функции вида 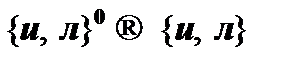 (табл. 2) и ровно четыре функции вида
(табл. 2) и ровно четыре функции вида 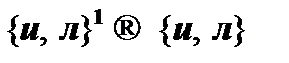 (табл. 3).
(табл. 3).
В табл. 2первая функция представляет собой нульместную константу «истина»,
а вторая – нульместную константу «ложь». Их надо рассматривать просто как другие обозначения для «истины» и «лжи».
| Таблица 3 | ||||
| p | 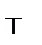
| p | 
| 
|
| <и> | и | и | л | л |
| <л> | и | л | и | л |
В табл. 3 приведены все одноместные функции. Первая и последняя – это уже знакомые нам константные функции «истина» и «ложь», т. е. переменная p является фиктивной. Вторая функция – это функция, значение которой совпадает со значением ее аргумента. Третья функция задает унарную связку отрицание.
Существует ровно 16 двухместных булевых функций вида  (табл. 4).
(табл. 4).
Таблица 4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| p | q | 
| 
| 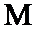
| p | 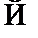
| q | 
| 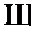
| 
| 
| 
| 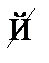
| 
| 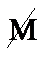
| 
| 
|
| и | и | и | и | и | и | и | и | и | и | л | л | л | л | л | л | л | л |
| и | л | и | и | и | и | л | л | л | л | и | и | и | и | л | л | л | л |
| л | и | и | и | л | л | и | и | л | л | и | и | л | л | и | и | л | л |
| л | л | и | л | и | л | и | л | и | л | и | л | и | л | и | л | и | л |
В этой таблице первая и последняя функции – это константные функции; 4 и 6 – это функции, сохраняющие значение соответствующего аргумента; 11 и 13 – это функции отрицания соответствующих аргументов. Среди оставшихся 2, 5 и 8 – это функции, которые задают точный смысл исходных классических двухместных логических связок: нестрогой дизъюнкции, материальной импликации и конъюнкции; 7, 10, 15 – это функции, задающие точный смысл материальной эквиваленции, строгой дизъюнкции и связки Нико; функция 3 – это обратная импликация; функции 12 и 14 – это соответственно антиимпликация и обратная антиимпликация; функция 9 называется функцией Шефера.
Перечисленные пропозициональные связки имеют важную особенность: значения сложных высказываний, образованных с их помощью, зависят только от значений тех выражений, из которых образованы сложные. Таким образом, зная значения А и В, можно однозначно установить значения выражений, образованных с помощью соответствующих логических связок. Это позволяет рассматривать данные символы как знаки функций истинности. Соответствующие им пропозициональные связки называются истинностно-функциональными.
Алгоритм построения таблиц истинности. Построение таблицы истинности для произвольной формулы А предполагает последовательное осуществление следующих действий:
1. Выделить все пропозициональные переменные, входящие в состав А.
2. В столбик выписать все возможные наборы значений переменных.
3. В составе формулы А выделить все подформулы (начиная от элементарных
и кончая самой формулой А).
4. Вычислить значение каждой подформулы при каждом наборе значений переменных.
5. Вычислить значение по главной связке.
| Таблица 5 | ||||
| p | q | 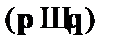
| 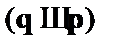
| 
|
| и | и | и | и | и |
| и | л | л | л | и |
| л | и | л | л | и |
| л | л | л | л | и |
При вычислении значений сложных подформул используются табличные определения связок. Например, нам дана формула: 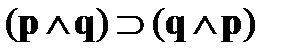 . Данная формула содержит две пропозициональных переменных – pи q. Тогда каждая переменная принимает одно из двух значений – {и, л}. Отсюда следует, что таблица должна содержать четыре строки. Подформулами являются выражения:
. Данная формула содержит две пропозициональных переменных – pи q. Тогда каждая переменная принимает одно из двух значений – {и, л}. Отсюда следует, что таблица должна содержать четыре строки. Подформулами являются выражения:  и
и  . Главная связка –
. Главная связка –
« 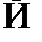 » (табл. 5).
» (табл. 5).
| Таблица 6 | ||||
| p | q | | ||
| и | и | и | и | и |
| и | л | л | и | л |
| л | и | л | и | л |
| л | л | л | и | л |
Таблица для формулы может быть построена более
компактно, для чего необходимо лишь выписать в ее отдельные столбцы элементарные подформулы (для них задаются все возможные наборы значений), значения же сложных подформул указываются под их главными знаками в составе формулы. Значение самой формулы указывается под ее
главным знаком, данный столбец таблицы называется результирующим (табл. 6).
Законом классической логики высказываний является формула, принимающая значение «истина» при любых наборах значений входящих в нее пропозициональных переменных. Рассмотренная выше формула как раз и является таким законом. Формулы данного типа называют тождественно-истинными или общезначимыми. Утверждение «формула А является тождественно-истинной» сокращенно записывается в метаязыке следующим образом: « 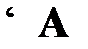 ».
».
Формула называется тождественно-ложной, если и только если она принимает значение «ложь» при любых наборах значений входящих в нее пропозициональных переменных.Любое отрицание тождественно-истинной формулы дает тождественно-ложную форму.
Формулы, принимающие значение «истина» или «ложь», по крайней мере, при одном наборе значений входящих в нее пропозициональных переменных, называются соответственно выполнимыми или опровержимыми.
Логически истинным будет высказывание, если его формула примет значение «истина» во всех строках таблицы. Логически ложным будет высказывание, формула которого принимает значение «ложь» при любом наборе переменных. Остальные высказывания именуются логически недетерминированными.
Все логические связки, введенные в табл. 5, не являются независимыми друг от друга. Через исходные связки можно ввести в язык классической логики высказываний любую связку, являющуюся знаком функции истинности. Как правило, язык пропозициональной логики может быть задан всего лишь при помощи пары связок. Однако две связки являются функционально полными – это функция Шеффера и функция Пико. Данные связки по отдельности позволяют выразить любые другие.
Дата добавления: 2018-04-05; просмотров: 1433; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!