ЭНЕРГИТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
Министерство образования и науки Росссийской Федерации
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский технологический университет «МИСиС»
НОВОТРОИЦКИЙ ФИЛИАЛ
Кафедра оборудование металлургических предприятий
Т.В. Степыко
Сопротивление материалов
Методическое пособие для проведения практических занятий
Для студентов направлении: 150400 «Металлургия»,
151000 «Технологические машины и оборудование»,
140100 «Теплоэнергетика и теплотехника»,
240100 «Химическая технология»,
140400 «Электроэнергетика и электротехника»,
очной и заочной форм обучения
Новотроицк, 2014
УДК 539.3/6
Рецензенты:
Начальник цеха сервисного обслуживания сталеплавильного производства ОАО «Уральская Сталь» Прохоров А.В.
Зав. кафедрой оборудование металлургических предприятий ФГАОУ ВПО «Национальный исследовательский технологический университет «МИСиС», Новотроицкий филиал, к.п.н. Нефедов А.В.
Степыко Т.В. Сопротивление материалов: Методическое пособие для проведения практических занятий. – Новотроицк: НФ НИТУ «МИСиС», 2014. – 93с.
Предназначено для студентов, обучающихся по направлениям подготовки бакалавров 150400 «Металлургия», 151000 «Технологические машины и оборудование», 140100 «Теплоэнергетика и теплотехника», 240100 «Химическая технология», 140400 «Электроэнергетика и электротехника», очной и заочной формы обучения.
|
|
|
Рекомендовано Методическим Советом НФ НИТУ «МИСиС».
© Новотроицкий филиал
ФГАОУ ВПО «Национальный
исследовательский технологический университет «МИСиС», 2014
СОДЕРЖАНИЕ
| Введение……………………………………………………………………... | 4 |
| 1 Анализ внутренних силовых факторов………………………………….. | 5 |
| 1.1 Теоретическая часть……………………………………………… | 5 |
| 1.2 Практическая часть………………………………………………. | 7 |
| 1.3 Вопросы для самопроверки……………………………………… | 9 |
| 2 Растяжение и сжатие……………………………………………………… | 10 |
| 2.1 Теоретическая часть……………………………………………… | 10 |
| 2.2 Практическая часть………………………………………………. | 13 |
| 2.3 Вопросы для самопроверки……………………………………… | 20 |
| 3 Прямой изгиб……………………………………………………………… | 21 |
| 3.1 Теоретическая часть……………………………………………… | 21 |
| 3.2 Практическая часть………………………………………………. | 24 |
| 3.3 Вопросы для самопроверки……………………………………… | 32 |
| 4 Энергетические методы определения перемещений…………………… | 33 |
| 4.1 Теоретическая часть……………………………………………… | 33 |
| 4.2 Практическая часть………………………………………………. | 36 |
| 4.3 Вопросы для самопроверки……………………………………… | 47 |
| 5. Основы теории напряженного и деформированного состояния………. | 48 |
| 5.1 Теоретическая часть……………………………………………… | 48 |
| 5.2 Практическая часть……………………………………………….. | 50 |
| 5.3 Вопросы для самопроверки……………………………………… | 55 |
| 6 Сдвиг и кручение………………………………………………………….. | 57 |
| 6.1 Теоретическая часть……………………………………………… | 57 |
| 6.2 Практическая часть………………………………………………. | 59 |
| 6.3 Вопросы для самопроверки……………………………………… | 62 |
| 7 Метод сил………………………………………………………………….. | 64 |
| 7.1 Теоретическая часть……………………………………………… | 64 |
| 7.2 Практическая часть………………………………………………. | 65 |
| 7.3 Вопросы для самопроверки……………………………………… | 71 |
| 8 Сложное сопротивление………………………………………………….. | 72 |
| 8.1 Теоретическая часть……………………………………………… | 72 |
| 8.2 Практическая часть………………………………………………. | 73 |
| 8.3 Вопросы для самопроверки……………………………………… | 77 |
| 9 Устойчивость продольно сжатых стержней…………………………….. | 79 |
| 9.1 Теоретическая часть……………………………………………… | 79 |
| 9.2 Практическая часть………………………………………………. | 81 |
| 9.3 Вопросы для самопроверки……………………………………… | 84 |
| Задачи для выполнения контрольных и домашних работ……………….. | 85 |
| Список используемых источников………………………………………… | 92 |
ВВЕДЕНИЕ
|
|
|
|
|
|
В методическом пособии рассматриваются темы практических занятий, охватывающие основные разделы курса сопротивления материалов: построение эпюр внутренних усилий для стержней, валов, балок, ломаных стержней и рам, кривых брусьев, расчеты на прочность и жесткость при растяжении и сжатии, кручении; определение деформаций балок при изгибе; статически неопределимые задачи изгиба балок; определение перемещений в балках и рамах, расчет рам методом сил; теория напряженного и деформированного состояния, сложное сопротивление; устойчивость сжатых стержней.
Все практические занятия предваряются кратким изложением соответствующего теоретического материала. В пособии использована Международная система единиц (СИ). Обозначения величин приняты в соответствии с международными рекомендациями ИСО. Примеры могут быть использованы студентами при выполнении домашних и контрольных работ.
|
|
|
АНАЛИЗ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ
Теоретическая часть
При изучении классификации внешних сил (нагрузок) следует отчетливо представлять их разновидности в зависимости от способа их приложения – объемные и поверхностные. Поверхностные нагрузки делят на распределенные и сосредоточенные. По характеру действия нагрузки делят на статические и динамические. Необходимо разбираться в разновидностях каждой из нагрузок и суметь привести пример на каждую из них.
Нагрузки, действующие на тело, вызывают в нем деформации. Тело, деформации которого рассматриваются, имеет форму бруса, т.е. тела, у которого длина значительно больше линейных размеров поперечного сечения. Если деформация после прекращения действия сил на тело исчезает, то такая деформация называется упругой. Неисчезающие деформации называются остаточными или пластическими, такие деформации в машинах и сооружениях, как правило, не допускаются.
Внешние силы (нагрузки), действующие на брус, вызывают возникновение в нем внутренних сил (сил упругости). Для определения внутренних сил пользуются методом сечений, который позволяет определить внутренние силы в том или ином сечении тела, и заключается в следующем: брус, находящийся в равновесии, разрезают (мысленно) на две части, отбрасывают одну из частей, заменяют действие отброшенной части на оставшуюся внутренними силами и составляют уравнения равновесия для оставшейся части, на которую действуют приложенные к ней внешние и внутренние силы. Действующая в проведенном поперечном сечении система внутренних сил эквивалентна в общем случае одной силе и одному моменту. Разложив их на составляющие, получим соответствующие три силы (по направлению координатных осей Qx, Qy, Nz) и три момента (относительно этих осей Мх, Мy, Mz), которые называют внутренними силовыми факторами (ВСФ)
Рисунок 1- Распределение ВСФ
Возникновение тех или иных ВСФ зависит от фактического нагружения бруса. Определяют ВСФ с помощью уравнений равновесия статики (рисунок 1).
1 ∑Fix=0 4 ∑Mx(Fi)=0
2 ∑Fiy=0 5 ∑My(Fi)=0
3 ∑Fiz=0 6 ∑Mz(Fi)=0
Надо хорошо усвоить, что внутренним нормальным силам соответствуют нормальные напряжения – σ (сигма), касательным силам касательные напряжения – τ (тау). Рисунок 2.
Рисунок 2- Распределение напряжений по сечению
Нормальное напряжение σ, действующее нормально, т.е. перпендикулярно к сечению, и касательное напряжение τ, действующее параллельно плоскости сечения или касательно к нему, являются составляющими полного напряжения р, величина которого равна: 
Напряжение выражает меру внутренних сил, возникающих в материале элемента конструкции.
Практическая часть
Задача 1.Построить эпюру продольных сил для жестко защемленной балки (рисунок 3).
Решение:
1 Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2 Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
I участок 0 ≤z1 ≤ 2 м
N1 = q1· z1,
При z1=0 N1=0
При z1 =2м N1=20 кН
II участок
N2 = q1· 2=10·2=20 кН
III участок
N3 = q1· 2 – F1 = 20 – 40 = - 20 кH,
IV участок 4 ≤ z4 ≤ 5 м
N4 = q1· 2 – F1 + q2· (z4-4),
При z4=4 м N4=-20 кН
При z4 =5 м N4=0
V участок
N5 = q1· 2– F1 – F2+ q2·1 = - 30 кH.
3 По найденным значениям строим эпюру Nz.
Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные - под осью.
Рисунок 3 - Эпюра продольных сил
Вопросы для самопроверки
1 Что такое деформация? Какие деформации называют упругими, и какие пластичными (остаточными)?
2 Что называется напряжением в данной точке сечения тела? На какие две составляющие может быть разложен вектор полного напряжения?
3 Что называется прочностью, жесткостью и устойчивостью детали (конструкции)?
4 В чем заключается сущность расчета на прочность и на устойчивость?
5 По каким признакам и как классифицируются нагрузки в сопротивлении материалов?
6 На каких гипотезах и допущениях основаны выводы расчетных зависимостей сопротивления материалов?
7 Сформулируйте принцип независимости действия сил в применении к сопротивлению материалу.
8 В чем заключается метод сечения? Какова цель применения метода сечений? Укажите последовательность операций при использовании метода сечений?
2 РАСТЯЖЕНИЕ И СЖАТИЕ
Теоретическая часть
Изучение темы необходимо начинать с выяснения вопроса о внутренних силовых факторах, действующих в сечении бруса. Применение метода сечений позволяет найти величину и направление равнодействующей внутренней (продольной) силы упругости в рассматриваемом сечении. Принято считать, что внутренняя растягивающая сила положительна, а сжимающая – отрицательна. Поэтому неизвестную продольную силу N всегда направляют от сечения (рисунок 4), предполагая, что в рассматриваемом сечении возникает растяжение. Величина продольной силы N определяется из условия равновесия отсеченной части, а именно: сумма сил, действующих по оси х, равна нулю при условии равновесия бруса.
Рисунок 4- Направление продольной силы N
SFix=F-N=0, и следовательно N=F.
Если при расчете продольная сила получается положительной, это значит, что она действительно направлена от сечения и является растягивающей. Если N получается отрицательной, то она является сжимающей.
При изучении растяжения и сжатия прямого бруса следует обратить особое внимание на гипотезу плоских сечений, которая справедлива и при других видах нагружения бруса.
Сущность ее заключается в том, что плоские сечения, нормальные к оси бруса до деформации, остаются и после деформации плоскими и нормальными к его оси, а отсюда следует, что продольные элементы бруса растягиваются одинаково, силы упругости будут распределяться по сечению бруса равномерно, а поэтому напряжение во всех точках сечения определяется по формуле
,
где N – внутренняя сила;
А – площадь поперечного сечения, которая является геометрической характеристикой прочности и жесткости, форма сечения значения не имеет, все точки сечения равноопасны.
Мерой деформации растяжения (ε) является относительное удлинение (рисунок 5).
Рисунок 5- Удлинение бруса
где ℓ – первоначальная длина бруса;
Δℓ=ℓ1- ℓ – абсолютное удлинение.
Величина ε не имеет размерности и часто выражается в процентах.
Особого внимания заслуживает закон Гука, согласно которому в пределах упругой деформации материала между напряжением и деформацией принимается прямо пропорциональная зависимость, которая выражается формулой:
, (1)
где σ – нормальное напряжение;
Ε – модуль продольной упругости (модуль упругости первого рода или модуль Юнга);
ε - относительное удлинение (или осевое укорочение).
Модуль продольной упругости имеет размерность напряжения МПа или Па, (1 МПа = 106 Па) и характеризует жесткость материала, его способность сопротивляться упругому деформированию.
Для участка бруса длиной l, на котором постоянны продольная сила и площадь поперечного сечения, закон Гука можно записать в виде:
(2)
Это вторая форма закона Гука. Произведение ЕА называют жесткостью сечения. При расчетах на растяжение и сжатие используют основной принцип прочности детали: действующие или расчетные напряжения ни в одной точке детали не должны превышать допускаемые напряжения.
Так как при растяжении (сжатии) во всех точках сечения напряжения одинаковы, то при расчете бруса на прочность определяют положение наиболее напряженного (опасного) поперечного сечения. Если брус имеет постоянное по его длине поперечное сечение, то опасным является сечение, в котором возникает наибольшая продольная сила N. Если значение продольной силы во всех сечениях одинаково, то опасным является сечение с наименьшей площадью. Для определения опасного сечения бруса при изменяющихся по его длине площади поперечного сечения и продольной силе необходимо строить эпюру нормальных напряжений.
Условие прочности бруса при растяжении (сжатии), составленное для опасного сечения, имеет вид:
(3)
Условие прочности в словесной форме можно записать следующим образом:
| Действующее (расчетное) напряжение |
=
| Внутреннее усилие | ≤ | Допускаемое напряжение |
| Характеристика поперечного сечения |
Форма сечения бруса не влияет на его прочность при растяжении (сжатии). Форму сечения бруса необходимо знать только для определения размеров сечения при известном сечении площади.
С помощью условия прочности выполняют три вида расчетов: проверочный расчет, проектный расчет и определение допускаемой нагрузки.
Надо знать, что в ряде случаев необходимые для расчета бруса усилия невозможно найти только из уравнений равновесия. Такие задачи называют статически неопределимыми. При решении таких задач уравнения, которых не хватает для определения усилий, составляют из условия деформации бруса или системы.
Практическая часть
Задача 1.Ступенчатый стержень круглого поперечного сечения нагружен силами 
. Принимаем материал стержня 
, 
, 
.
Определить:
1 Необходимые размеры попречных сечений бруса;
2 Нормальные напряжения;
3 Перемещения поперечных сечений.
Решение:
1 Построим эпюры продольных сил.
Схема нагружения стержня представлена на рисунке 6. Обозначим сечения, в которых приложены силы и меняются размеры стержня буквами, начиная от А до F. Сечениями, где приложены силы, стержень разбивается на три участка, в пределах которых продольная сила постоянная, поэтому для определения ее значений нужно рассечь каждый участок и из условия равновесия отсеченной части, не содержащей заделку, определить величину продольной силы.
Проведем на участке АВ произвольное сечение I-I, отбросим часть стержня, содержащую заделку, и рассмотрим условие равновесия оставшейся правой части. На рассматриваемую часть стержня действует сила Р3 = 20кН и продольная сила N1 в сечении I-I. При определении продольных сил в сечениях предполагаем, что они растягивают рассматриваемую часть стержня, т.е. направлены от сечения.
Проектируя силы на ось Х, получим N1 - Р3 = 0. Откуда N1 =Р3 =20 кН.
Т.к. продольная сила N1 получилась с положительным знаком, то участок стержня АВ растягивается.
Проведем произвольное сечение II-II и рассмотрим равновесие отсеченной части стержня, не содержащей заделку.
,
N2 +Р2 - Р3 = 0
N2 = -Р2 + Р3 =20 -10 = 10 кН.
Положительный знак продольной силы N2 свидетельствует о том, что третий участок испытывает растяжение.
Проведем произвольное сечение III-III и рассмотрим равновесие отсеченной части стержня, не содержащей заделку.
,
N3 - Р1 +Р2 - Р3 = 0
N3 = Р1 - Р2 + Р3 =40 - 10 + 20 = 50 кН.
Рисунок 6 - Схема нагружения стержня
Положительный знак продольной силы N3 свидетельствует о том, что третий участок испытывает растяжение.
По найденным значениям продольных сил строим график (эпюру) изменения продольных сил по длине стержня. Проводим базу эпюры параллельно оси стержня и в выбранном масштабе откладываем вверх положительные значения продольных сил и вниз отрицательные.
При правильно построенной эпюре продольных сил в сечениях, где приложены сосредоточенные силы на эпюре будут иметь место скачки на величину приложенной силы.
2 Определим необходимые размеры попречных сечений бруса.
Необходимые размеры поперечних сечений бруса определим исходя из условии прочности при растяжении.
Определим площади сечений на каждом участке
;
; 
; 
.
Значение напряжений на каждом участке
; 
; 
; 
; 
; 
.
Выразим диаметр на участке где продольные силы имеют большее значение.
;
;
;
.
Округляем диаметры до ближайшего целого большего числа.
; 
; 
; 
.
3 Построение эпюр нормальних напряжений.
;
;
;
;
;
.
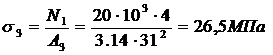По этим данным строим эпюру нормальных напряжений.
4 Построение эпюры перемещений поперечных сечений.
Деформация бруса на каждом участке:
;
;
;
;
.
Перемещения в сечениях:
;
;
;
;
;
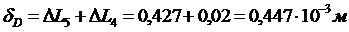4 Определим необходимую толщину и диаметр головки стержня:
; 
На срез ось рассчитываем по формуле:
;
На смятие ось рассчитываем по формуле:
;
Принимаем диаметр головки стержня D=41мм;
Принимаем толщину головки стержня h=8мм.
Задача 2.Дано: l=1м; l/L=0.3; С/L=0,52; λ/L=0,6; F1/F=1,2; F2/F=1,2; Р1/Р=3; Р2/Р=4; 
; Р=10 кН; Е=1×105 МПа.
Определить: N, σ, ΔL.
Рисунок 7 – Схема нагружения стержня
Задача 3.Дано: 
; а=2,7м; b=3.7м; с=1,3м; α=45°; [σ]=160МПа; 
; n=1,5.
Раскрыть статическую неопределимость стержневой системы.
Решение:
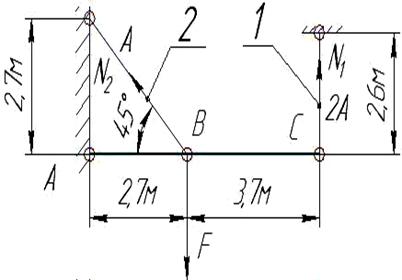
Рисунок 8 - Статически неопределимая стержневая система
Вопросы для самопроверки
1 Как можно нагрузить прямой брус, чтобы он работал только на растяжение (сжатие)?
2 Какие внутренние силовые факторы возникают в поперечном сечении стержня при его растяжении или сжатии?
3 Как строится эпюра продольных сил?
4 Что такое продольная и поперечная деформация бруса при растяжении (сжатии) и какова зависимость между ними?
5 По какой формуле определяется величина напряжения в поперечном сечении стержня?
6 Сформулируйте закон Гука и приведите формулу, выражающую этот закон.
3 ПРЯМОЙ ИЗГИБ
Теоретическая часть
Приступая к изучению этой темы необходимо уяснить, что теория изгиба построена при следующих допущениях и предположениях (рисунок 9):
Рисунок 9 - Схема нагружения бруса
1 геометрическая ось бруса, т.е. ось, проходящая через центры тяжести сечений, есть прямая линия;
2 внешние силы, изгибающие брус, лежат в одной плоскости, проходящей через геометрическую ось бруса и все нагрузки перпендикулярны к геометрической оси бруса
- плоскость действия нагрузок является плоскостью симметрии бруса;
- поперечные сечения бруса, плоские до деформации изгиба, остаются плоскими и после деформации;
3 деформации бруса незначительны.
Изгибом называют такой вид деформации бруса, при котором в его поперечных сечениях возникают два силовых фактора – поперечная сила Q и изгибающий момент Мx, для определения численных значений, которых используется метод сечений. Необходимо помнить, что поперечная сила в данном сечении равна алгебраической сумме внешних сил, расположенных только по одну сторону (справа или слева) от рассматриваемого сечения, а изгибающий момент в данном сечении равен алгебраической сумме моментов внешних сил (расположенных слева или справа от сечения), взятых относительно центра тяжести сечения. При этом надо понять и строго придерживаться правила знаков для поперечной силы и изгибающего момента. Поперечная сила считается положительной, если внешние силы стремятся сдвинуть левую часть балки относительно правой вверх или правую часть балки относительно левой – вниз. Правило для поперечной силы показано на рисунке 10.
Рисунок 10 - Правило знаков поперечной силы Q при изгибе
Правило знаков для изгибающих моментов: внешним моментам, изгибающим мысленно закрепленную в рассматриваемом сечении отсеченную часть балки выпуклостью вниз, приписывается знак плюс, а моментам, изгибающим отсеченную часть балки выпуклостью вверх – знак минус.
Рисунок 11- Правило знаков изгибающего момента МХ при изгибе
Следует научиться свободно, строить эпюры поперечных сил и изгибающих моментов. Для проверки правильности построения эпюр целесообразно пользоваться теоремой Журавского, устанавливающей зависимость между изгибающим моментом и поперечной силой:
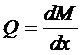, (4)
т.е. поперечная сила равна производной от изгибающего момента по абсциссе сечения х.
Интенсивность распределения нагрузки:
, (5)
т.е. вторая производная от изгибающего момента по абсциссе сечения х равна интенсивности распределенной нагрузки.
Необходимо уметь выводить формулу для определения нормальных напряжений в производной точке сечения балки:
, (6)
где М – изгибающий момент в данном сечении балки;
у – расстояние точки сечения от нейтральной оси;
Ix – осевой момент инерции сечения балки.
Из формулы для определения нормальных напряжений в производной точке можно получить расчетное уравнение на изгиб. Обозначив допускаемое напряжение на изгиб [σ], получим расчетное уравнение:
, (7)
где Мmax – наибольший изгибающий момент в сечении балки;
Wx – осевой момент сопротивления сечения.
Условие прочности позволяет выполнять три вида расчетов: проверочный расчет балки на прочность, определение допускаемых размеров сечения и расчет допускаемых действующих на балку нагрузок.
После этого следует перейти к изучению вопроса об определении углов поворота поперечных сечений и прогибов балок. Для их определения целесообразно использовать универсальные уравнения.
Линейное перемещение «у» центра тяжести сечения называется прогибом. Наибольший прогиб обозначают f. Сечение балки поворачивается вокруг нейтральной линии сечения на некоторый угол φ, который называется углом поворота сечения. Условие жесткости при изгибе записывают в виде:
f ≤ [f]; φmax ≤ [φ]
Допускаемый прогиб назначают в долях пролета балки ℓ.
Для валов принимают [f] = ( 0,0002 – 0,0010) ℓ.
Допускаемые углы поворота сечений вала в местах, где расположены подшипники, принимают в пределах 0,001 – 0,005 рад.
Практическая часть
Задача 1.Дано: l=2,4м; F=12кН; q=10кН/м; М=6кНм.
Определить номер двутавра, прогиб в середине пролета.
Решение:
Схема нагружения балки представлена на рисунке 12. Определим опорные реакции, записывая уравнения моментов всех сил, приложенных к балке, относительно точек А и В.
МА=0 
МВ=0 
Рисунок 12- Схема нагружения балки
Проверка: 
Положительные знаки опорных реакций свидетельствуют о том, что предполагаемое направление соответствует истинному. Возьмем на балке характерные сечения и вычислим в них величины Q и М.
Определение значений поперечной силы в характерных сечениях.
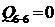
По найденным значениям поперечных сил построена эпюра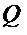 
.
Определение величин изгибающих моментов в характерных сечениях.
По найденным значениям моментов строим эпюру изгибающих моментов Мx.
Из эпюры изгибающих моментов находим опасное сечение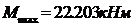 
Из условия прочности 
Найдем необходимый момент сопротивления сечения
По сортаменту (ГОСТ 8239-72) принимаем двутавр № 20 с Wx = 184 см3 
; 
; 
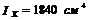Опасное сечение в точке, где М=22.2кНм, Q=12.25кН.
Определим максимальные, нормальные напряжения
Максимальные касательные напряжения
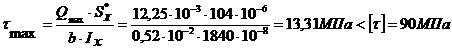
Определяем напряжения в опасном сечении в точке С по формуле
По найденным данным строим эпюры напряжений.
Определим перемещение точки К балки.
Граничные условия имеют следующий вид:
при Х = 0; 
при Х = 4,8м.
Левая опора совпадает с началом координат 
. Следовательно, один из начальных параметров определен.
В уравнение должно войти все внешние усилия расположенные левее точки В.
Для определения прогиба в точке К при х = 2,4м составим уравнение:
Таким образом точка К перемещается вниз на 1,17см.
Анализируя эпюру Mx видим, что на участке 0-1 растянуты нижние волокна, и поэтому на этом участке изогнутая ось балки будет иметь выпуклость вниз. В точке, где Mx = 0, будет точка перегиба. На участке 1-2 растянуты верхние волокна, и изогнутая ось балки будет иметь выпуклость вверх. На участке 3-4 растянуты нижние волокна, и изогнутая ось балки будет иметь выпуклость вниз. В точке, где Mx = 0, будет точка перегиба. Учитывая все сказанное и то, что прогибы в опорных сечениях равны нулю, строим приблизительный вид изогнутой балки (рисунок 13).
Рисунок 13 - Приблизительный вид изогнутой балки
Задача 2.Дано: В предыдущей задаче мы выбрали сечение балки состоящее из двутавра №10 с 
; Wx = 39,7 см3
Определим прогибы балки.
Решение:
В точке 1 прикладываем единичную силу, от нее определяем реакции опор и строим эпюру изгибающих моментов, которую «перемножаем» на эпюру М (рисунок 14).
Знак «плюс» указывает на то, что точка 1 перемещается по направлению единичной силы, т.е. вниз.
В точке 2 прикладываем единичную силу, от нее определяем реакции опор и строим эпюру изгибающих моментов, которую «перемножаем» на эпюру М.
Знак «плюс» указывает на то, что точка 2 перемещается по направлению единичной силы, т.е. вниз.
Определим углы поворотов поперечных сечений балки.
В точке 1 прикладываем единичный момент, от него определяем реакции опор и строим эпюру изгибающих моментов, которую «перемножаем» на эпюру М.
Рисунок 14 – Точка перегиба и изогнутая ось балки
Знак «плюс» указывает на то, что сечение в точке 1 поворачивается по часовой стрелке.
Задача 3.Для заданных двух схем балок (рисунок 15) требуется написать выражения Qу , Мх для каждого участка в общем виде, построить эпюры Qу , Мх, найти 
и подобрать:
Схема а Схема б
Рисунок 15 - Плоский изгиб
для схемы а: деревянную балку круглого поперечного сечения при 
МПа;
для схемы б: стальную балку двутаврового поперечного сечения при 
МПа.
Исходные данные: М = 20 кН·м; Р = 20 кН; q = 8 кН/м; L1=12 м; L2=8м; а1/a=2; а2/a=8; а3/a=3.
Вопросы для самопроверки
1 Дайте определение понятия «прямой чистый изгиб», «прямой поперечный изгиб».
2 Как находится изгибающий момент в каком-либо сечении балки?
3 Как находится поперечная сила в каком-либо сечении балки? Когда поперечная сила считается положительной?
4 Какой случай называется чистым изгибом?
5 Напишите формулу для определения нормального напряжения в произвольной точке поперечного сечения бруса, работающего на изгиб. Какой момент инерции входит в указанную формулу?
6 Как записывается условие прочности при изгибе?
7 Что называется осевым моментом сопротивления?
8 Напишите формулы для определения осевых моментов сопротивления круга, кольца, прямоугольника.
9 Какие формы поперечных сечений рациональны для балок из пластичных материалов?
10 Какие формы поперечных сечений следует применять для чугунных балок?
11 В каких плоскостях возникают касательные напряжения при изгибе? Как находится их величина?
12 Как записывается дифференциальное уравнение натянутой оси балки?
13 Как находят прогиб балки графо-аналитическим методом?
14 Напишите универсальное уравнение для определения перемещений при изгибе.
15 В чем состоит сущность расчета на жесткость при изгибе?
ЭНЕРГИТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
Теоретическая часть
Статически неопределимые балки и рамы – конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Такими связями могут быть как опорные связи, так и стержни самой конструкции. Будем рассматривать балки и простые рамы, то есть такие конструкции, в которых связями, обеспечивающими геометрическую неизменяемость, являются опорные закрепления (опорные связи). Для обеспечения геометрической неизменяемости балки (рамы) в плоскости достаточно трех связей. Каждая связь запрещает какое-то перемещение. Шарнирно-подвижная опора запрещает перемещение по направлению, перпендикулярному плоскости опирания, и является одной связью. Шарнирно-неподвижная опора делает невозможными линейные перемещения по двум взаимно-перпендикулярным направлениям (вертикальному и горизонтальному) и соответствует двум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемления на конце стержня становятся невозможными все перемещения: и вертикальное, и горизонтальное, и угол поворота, поэтому, жесткое защемление представляет собой три связи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждая дополнительная связь сверх трех для плоских систем превращает конструкцию в статически неопределимую. Такие дополнительные связи, которые не являются необходимыми для обеспечения геометрической неизменяемости конструкции, называются лишними.
Оговоримся, что здесь и далее понятие «расчет» подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.
Статически неопределимые системы обладают рядом характерных особенностей:
1. Статически неопределимая система ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически определимой системой оказывается более жесткой;
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках;
3. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе;
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы;
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости;
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.
Основными методами расчета статически неопределимых систем являются:
1. Метод сил. При расчете по методу сил основными искомыми величинами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы;
2. Метод перемещений. При расчете по методу перемещений основными искомыми величинами являются перемещения узловых точек, вызванные деформацией системы. Знание этих перемещений необходимо и достаточно для определения всех внутренних усилий, возникающих в поперечных сечениях элементов, заданной системы;
3. Метод конечных элементов. При расчете по методу конечных элементов система разбивается на простые конечные элементы и по матрице жесткости элемента и системы в целом устанавливается связь между перемещениями узлов элемента и системы и усилиями в них;
4. Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения;
5. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитических методов при расчете особо сложных систем используются различные численные методы.
Кроме указанной классификации, методы расчета статически неопределимых систем можно расчленить по степени их точности, по области работы материала сооружений, по особенностям расчетных операций и т.д.
По степени точности различают точные и приближенные методы расчета.
Точные методы базируются на обычных основных допущениях, принятых при расчете достаточно жестких сооружений (закон Гука, расчет по деформированной схеме, принцип сложения действия сил). Приближенные методы расчета, кроме обычных упрощений, используют дополнительные допущения, что обусловливает заметное отклонение от результатов точных методов расчета.
По области работы материала различают расчет сооружений в упругой стадии и расчет сооружений за пределом упругости. По особенностям расчетных операций методы расчета можно разделить на вычислительные и экспериментальные.
Практическая часть
Задача 1.Дано: L = 4,5 м, q = 40 кН/м, Р = 150 кН, М = 15 кНм, 
, 
, 
Решение:
1 Расчет начинаем с определения степени статической определимости. Так как неизвестных реакций четыре, а уравнений равновесия можно составить три, то задача один раза статически не определима.
2 Для неразрезной балки в качестве основной системы выбираем такую же балку но с врезанными шарнирами на промежуточной опоре в шарнирах (рисунок 16).
3 К основной системе приложим заданную нагрузку, определяем реакции опор и построим эпюры изгибающих моментов от заданной нагрузки.
Участок АВ
Участок ВС
Рисунок 16 - Статически неопределимая балка
4 Снимаем заданную нагрузку, прикладываем Х1=1 и строим эпюру изгибающих моментов.
5 Составим каноническое уравнение
6 Определим коэффициенты канонического уравнения.
Перемножим эпюру М1 саму на себя
Перемножим эпюру М1 и Мр
7 Решим каноническое уравнение.
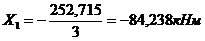
8 К каждой из балок прикладываем заданную нагрузку и найденный момент. От них определяем реакции опор и строим эпюры Q и М.
Участок АВ
Участок ВС
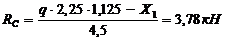
9 Выполним деформационную проверку.
Перемножим эпюру М1 и Мs
10 Из эпюры изгибающих моментов находим опасное сечение 
Из условия прочности 
Найдем необходимый момент сопротивления сечения
Для одного швеллера 
По таблице сортамента выбираем швеллер №33 ГОСТ 8239 
.
11 Определим прогиб и угол поворота в заданных сечениях.
В точке К прикладываем единичную силу, от нее определяем реакции опор и строим эпюру изгибающих моментов, которую «перемножаем» на эпюру М.
Знак «плюс» указывает на то, что точка К перемещается по направлению единичной силы, т.е. вниз.
Рисунок 17 - Прогиб и угол поворота в заданных сечениях
В сечении L прикладываем единичный момент, от него строим эпюру изгибающих моментов, которую «перемножаем» на эпюру М.
Знак «плюс» указывает на то, что сечение в L поворачивается в направлении единичного момента, т.е. по часовой стрелке.
Задача 2.Для статически неопределимой балки (рисунок.18, а) требуется:
1) раскрыть ее статическую неопределимость;
2) построить эпюру изгибающих моментов от действия внешних (пролетных) нагрузок;
3) подобрать двутавровое сечение балки из условия ее прочности;
4) определить угол поворота сечения L и прогиб балки в сечении К.
Дано: q = 6кН/м; m = 4кНм; а = 1,2м; [s] = 160МПа; E = 2∙105 МПа.
Рисунок 18- Статически неопределимая балка:
а - заданная система; б - основная система; в - эквивалентная система;
г - грузовая эпюра Mp; д - единичная эпюра М1; е - эпюра;
ж - окончательная эпюра M; з - эпюра от единичного момента Мm;
и - эпюра от единичной силы МР
Решение:
1 Вычисляем степень статической неопределимости балки.
По условиям закрепления имеем четыре опорных реакции: две на опоре А и по одной на опорах В и С. Для плоской системы сил можно составить только три уравнения равновесия, поэтому степень статической неопределимости балки n = 4‑3 = 1, т.е. система один раз статически неопределима.
2 Выбираем основную систему.
Для этого разрезаем балку над средней опорой, тем самым, устраняя лишнюю связь, и вставляем над опорой промежуточный шарнир. «Лишней» неизвестной в этом случае будет изгибающий момент в опоре В, который обозначаем Х1. На рисунке18,б показана основная система. Загружая основную систему пролетными нагрузками и лишней неизвестной, получаем эквивалентную систему (рисунок 18,в). Достоинство принятой основной системы в том, что каждый пролет работает как самостоятельная балка и при построении эпюр может рассматриваться отдельно.
3 Строим в основной системе эпюру изгибающих моментов от заданной нагрузки Mp.
Рассмотрим участок АВ. Так как на этом участке нагрузок нет, для построения эпюры достаточно знать величины изгибающих моментов в сечениях А и В. На опоре А по условию М = m = 4 кНм; на опоре В изгибающий момент равен нулю (опорный момент Х1 не учитываем), эпюра моментов ограничена прямой линией.
Рассмотрим участок ВС.
Вследствие симметрии пролетной нагрузки реакции опор будут одинаковыми:
Изгибающий момент в произвольном сечении x
и эпюра изгибающего момента ограничена квадратной параболой.
Строим эту параболу по трем лежащим на ней точкам:
xB = 0, MB= 0;
x = 1,2 м, 
xc = 2,4 м, Mc= 0.
Эпюра Мp показана на рис.3, г.
4 Строим эпюру 
от единичного момента 
.
В сечениях А и С изгибающие моменты равны нулю, а в сечении В изгибающий момент равен единице. Эпюра 
линейна, ее вид показан на рис.3, д.
5 Составляем каноническое уравнение метода сил
и вычисляем коэффициент δ11 при неизвестном. Для этого эпюра умножается сама на себя. Чтобы упростить вычисления, разбиваем эпюру на два треугольника ADB и BDC и площадь каждого из них умножаем на ординату, расположенную в центре тяжести каждого из них (рисунок 18, д):
После подстановки числовых значений имеем
Для определения ∆1р перемножаем эпюры МP и (рисунок 18, г, д)
Площадь параболического сегмента вычисляется по формуле:
где q - интенсивность распределенной нагрузки; l - длина участка балки под нагрузкой.
Вычисляем свободный член канонического уравнения ∆1р:
Произведя соответствующие вычисления, получаем
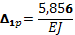
Тогда каноническое уравнение принимает вид
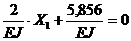
откуда находим
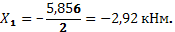
Отрицательное значение X1 говорит о том, что следует изменить направление момента X1 на обратное.
6 Строим эпюру изгибающих моментов.
Считая момент X1 внешней нагрузкой, можно определить опорные реакции, рассматривая каждый пролет балки отдельно, а затем построить эпюру моментов обычным способом, как это выполнялось для статически определимой балки. В данном случае удобнее воспользоваться уже построенными эпюрами.
Эквивалентная система находится под действием заданных пролетных нагрузок и вычисленного момента X1. Следовательно, окончательная эпюра изгибающих моментов может быть представлена суммой двух эпюр
M=Mp + Mx1.
Первая эпюра уже построена (рисунок 18, г), а вторая получается умножением ординат эпюры (рисунок 18, д) на вычисленное значение X1. Эпюра 
показана на рисунке 18,е. Геометрически складываем эпюры Мp и (рисунок 18, г, е), суммируя ординаты эпюр в характерных точках:
MA=4+0= 4 кН·м. ME=4,32-1,47= 2,85 кН·м.
MB= 0-2,93= -2,93 кН·м. MC=0.
По найденным значениям М строим окончательно эпюру изгибающих моментов (рисунок 18, ж).
Для проверки правильности расчетов и построения эпюры изгибающих моментов можно использовать условие равенства нулю угла поворота смежных сечений балки над средней опорой (перемещение по направлению отброшенной связи). Этот угол вычисляется перемножением окончательной эпюры моментов (рисунок 18, ж) на эпюру (рисунок 18, д). При перемножении эпюру М удобно представить в виде трех треугольников, показанных пунктирными линиями на рисунке 18, ж, и параболического сегмента.
Угол поворота смежных сечений балки над средней опорой вычислим методом перемножения эпюр:
Площади эпюр и соответствующие ординаты под их центрами тяжести
определяются по соответствующим эпюрам (рисунок 18, ж) и (рисунок 18,д).
Итак,
Полученный результат свидетельствует о том, что эпюра изгибающих моментов построена правильно. Небольшая погрешность, не превышающая 5% ,возникла в результате округлений.
7 Подбираем сечение балки по условию прочности.
При изгибе условие прочности имеет вид
По эпюре М (рис.18, ж) находим максимальный момент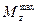 
= 4 кН·м, а по условию задачи [σ] = 160МПа. Подставляя эти числа в последнюю формулу, получим величину требуемого момента сопротивления двутавра:
По таблицам сортамента прокатной стали подбираем номер двутавра и выписываем его геометрические характеристики: двутавр №10, Wx= 39,7cм3, Jx = 198см4.
(Момент сопротивления подобранного двутавра больше требуемого расчетного, но меньшего размера в таблице нет, поэтому принимаем двутавр №10).
8 Определяем перемещения.
Определяем угол поворота сечения L.
Для этого приложим в сечении L основной системы единичный момент 
и построим эпюру моментов 
(рисунок 18 з). Угол поворота сечения L вычисляем, перемножая эпюры М и (рисунок 18 ж, з):
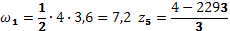
Определяем прогиб в сечении К.
Приложим в сечении К основной системы единичную силу Р=1 и построим от нее эпюру моментов 
р(рисунок 18, и). Так как сила Р=1 приложена в середине пролета AB, опорные реакции будут равны:
RA = RB = 0,5.
Определяем моменты в характерных точках участка АВ:
MA = 0; МK = 0,5∙1,8 = 0,9м; MB = 0.
Прогиб в сечении К вычисляется перемножением эпюр М и 
(рисунок 18, ж, и). Площадь при этом берем с эпюры М, а соответствующая ордината на эпюре 
равна величине средней линии трапеции, то есть алгебраической полусумме ее оснований:
Результат получен со знаком плюс, прогиб направлен в сторону приложенной единичной силы, то есть вниз.
Вопросы для самопроверки
1. Чем принципиально отличаются статически неопределимая балка от статически определимой?
2. Какие методы могут быть использованы для расчета статически неопределимых балок?
3. Как решают простейшие статически неопределимые балки?
4. Как записывается уравнение трех моментов?
5. Какие балки называют статически неопределимыми?
6. Какой порядок расчета используется при решении статически неопределимых балок?
7. Каким методом ведется проверка балки на жесткость?
8. Запишите условие прочности балки по нормальным напряжениям?
9. Объясните, как, используя условия прочности по нормальным напряжениям, подбираются балки из ГОСТа?
10. Для чего и как проводятся деформационная проверка при решении статически неопределимых балок?
Дата добавления: 2018-04-05; просмотров: 542; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!