Тема 4. Интегральные уравнения
§ 1. Типы интегральных уравнений
Линейные интегральные уравнения
Def Интегральное уравнение называется линейным, если в него неизвестная функция входит линейно.
 , где
, где  - искомая функция,
- искомая функция, 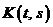 - ядро интегрального уравнения
- ядро интегрального уравнения  ,
, 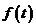 - свободный член интегрального уравнения,
- свободный член интегрального уравнения,  ,
,  - параметр.
- параметр.
Если уравнение дано, то функции 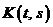 ,
, 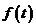 считаются заданными.
считаются заданными.
1.2. Уравнения Фредгольма
Различают интегральные уравнения Фредгольма I и II рода.
Def Интегральное уравнения Фредгольма II рода имеет вид
 .
.
Def Интегральное уравнения Фредгольма I рода имеет вид

(т.е. неизвестная функция вне интеграла отсутствует)
В уравнениях Фредгольма либо  ,
,  , либо удовлетворяет условиям если
, либо удовлетворяет условиям если 
 ,
,  .
.
Если 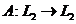 .
.
Ядра, удовлетворяющие  условию называются фредгольмовыми (или ядрами Гильберта-Шмидта).
условию называются фредгольмовыми (или ядрами Гильберта-Шмидта).
Интегральные уравнения различают однородные и неоднородные.
Def Интегральное уравнение называется однородным, если отсутствует свободный член 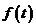 (или
(или  п.в. на
п.в. на  )
)
 .
.
В противном случае уравнение называется неоднородным.
1.3. Уравнения Вольтерра.
Различают уравнения Вольтерра I и II рода.
Def Уравнения Вольтерра II рода имеет вид
 ,
,  .
.
Def Уравнения Вольтерра I рода имеет вид
 ,
,  .
.
Аналогично уравнениям Фредгольма, среди уравнений Вольтерра различают однородные и неоднородные.
1.4. Связь уравнений Вольтерра с уравнениями Фредгольма.
Уравнение Вольтерра можно рассматривать как частный случай уравнения Фредгольма.
|
|
|
Ядро 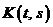 в уравнении Вольтерра
в уравнении Вольтерра

определено при  . Доопределим его при
. Доопределим его при  , положив
, положив  ,
,  .
.
Т.е. имеем уравнение Фредгольма с ядром
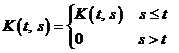

§ 2. Интегральный оператор Фредгольма.
2.1. Интегральный оператор в  .
.
Def Интегральным определением Фредгольма называется оператор вида
 , где
, где 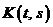 - ядро оператора.
- ядро оператора.
Теорема 1. Пусть  действует в
действует в  . Тогда если
. Тогда если  , то оператор
, то оператор  компактен.
компактен.
Теорема 2. Оператор  , компактен в
, компактен в  , если выполнены два условия
, если выполнены два условия
1) 
2) 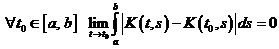 .
.
2.2. Интегральный оператор в 
Интегральный оператор Фредгольма можно рассматривать и как действующий в  .
.
Но тогда для компактности оператора, естественно, будут другие ограничения.
Теорема 1. Оператор  компактен в
компактен в  , если
, если  , т.е.
, т.е.  .
.
Оценка для нормы в этом пространстве выглядит так
 .
.
Теорема 2. Пусть дан оператор  в
в  . Тогда сопряженный ему оператор
. Тогда сопряженный ему оператор  определяется «сопряженным» ядром
определяется «сопряженным» ядром 

В частности, оператор  самосопряжен в
самосопряжен в  , т.е.
, т.е. 
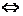
 .
.
§ 3. Альтернатива Фредгольма.
3.1. Операторные уравнения.
Заметим, что теоремы Фредгольма справедливы не только для интегральных уравнений, но и для более общих операторных уравнений с компактными операторами.
Поэтому выпишем как интегральные, так и операторные уравнения, участвующие в теоремах.
|
|
|
Интегральное уравнение Фредгольма II рода неоднородное
(1) 
Интегральное уравнение Фредгольма II рода однородное
(2) 
Интегральное уравнение Фредгольма II рода неоднородное, сопряженное
(3) 
Интегральное уравнение Фредгольма II рода однородное, сопряженное
(4)  .
.
Уравнение II рода неоднородное
(  )
) 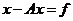
Уравнение II рода однородное
(  )
) 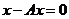
И, аналогично, сопряженные уравнения
(  )
) 
( 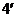 )
)  .
.
3.2. Теоремы Фредгольма.
Теорема 1 (Первая теорема Фредгольма)
Пусть  - компактный оператор в банаховом пространстве
- компактный оператор в банаховом пространстве 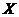 . Следующие утверждения эквивалентны:
. Следующие утверждения эквивалентны:
а) уравнение (  ) имеет решение и притом единственное
) имеет решение и притом единственное 
б) уравнение (  ) имеет только нулевое решение
) имеет только нулевое решение
в) уравнение (  ) имеет решение
) имеет решение 
г) уравнение ( 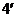 ) имеет только нулевое решение
) имеет только нулевое решение
Замечание 1. Утверждение об эквивалентности условий а) и б) называют альтернативой Фредгольма: либо уравнение (  )имеет
)имеет  единственное решение, либо однородное уравнение (
единственное решение, либо однородное уравнение (  )имеет ненулевое решение.
)имеет ненулевое решение.
Замечание 2. Если выполнено одно из условий а) –г) то операторы  и
и  имеют непрерывные обратные, т.е
имеют непрерывные обратные, т.е  ,
, 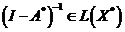 .
.
|
|
|
Теорема 2 (II теорема Фредгольма)
Пусть  - компактный оператор в
- компактный оператор в 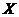 (банаховом). Тогда однородные уравнения (
(банаховом). Тогда однородные уравнения (  ) и (
) и ( 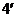 ) имеют одинаковое конечное число линейно независимых решений.
) имеют одинаковое конечное число линейно независимых решений.
Теорема 3 (III теорема Фредгольма)
Пусть  - компактный оператор в банаховом пространстве
- компактный оператор в банаховом пространстве 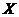 . Для того, чтобы при данном
. Для того, чтобы при данном  уравнение (
уравнение (  ) имело хотя бы одно решение, необходимо и достаточно, чтобы
) имело хотя бы одно решение, необходимо и достаточно, чтобы  было ортогонально, каждому решению
было ортогонально, каждому решению  уравнения (
уравнения ( 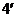 ), т.е.
), т.е.  .
.
Объединяя результаты теорем, можно сделать следующий вывод:
1) Либо уравнения (  ) и (
) и (  ) разрешимы при любых правых частях, и в этом случае уравнения (
) разрешимы при любых правых частях, и в этом случае уравнения (  ) и (
) и ( 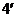 ) имеют лишь нулевые решения;
) имеют лишь нулевые решения;
2) Либо однородные уравнения (  ) и (
) и ( 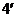 ) имеют одинаковое конечное число линейно независимых решений
) имеют одинаковое конечное число линейно независимых решений 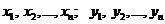 и в этом случае, чтобы уравнение (
и в этом случае, чтобы уравнение (  ) (соответственно
) (соответственно  ) имело решение, необходимо и достаточно, чтобы
) имело решение, необходимо и достаточно, чтобы  (соответственно
(соответственно  ).
).
Общие решения (  ) и (
) и (  ), соответственно, имеют вид
), соответственно, имеют вид
 и
и 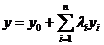 ,
,
где  и
и 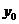 - соответственно какие-нибудь решения уравнений (
- соответственно какие-нибудь решения уравнений (  ) и (
) и (  ), а
), а  ,
,  - произвольные постоянные.
- произвольные постоянные.
3.3. Приложения к спектру компактного оператора.
В теоремах Фредгольма по существу речь идет об обратимости оператора  и эти теоремы означают, что
и эти теоремы означают, что  - или регулярная точка для
- или регулярная точка для  , или собственное значение конечной кратности. Разумеется, все, что утверждается в этих теоремах, остается справедливым и для операторов
, или собственное значение конечной кратности. Разумеется, все, что утверждается в этих теоремах, остается справедливым и для операторов  , если
, если  . Поэтому всякая отличная от нуля точка спектра компактного оператора является его собственным значением конечной кратности. Кроме того, мы знаем, что множество таких собственных значений не более чем счетно. Виду того, что компактный оператор не имеет ограниченного обратного в бесконечномерном пространстве, то
. Поэтому всякая отличная от нуля точка спектра компактного оператора является его собственным значением конечной кратности. Кроме того, мы знаем, что множество таких собственных значений не более чем счетно. Виду того, что компактный оператор не имеет ограниченного обратного в бесконечномерном пространстве, то 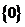 всегда принадлежит спектру компактного оператора в
всегда принадлежит спектру компактного оператора в  -мерном пространстве. Однако
-мерном пространстве. Однако 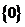 не обязан, вообще говоря быть собственным значением.
не обязан, вообще говоря быть собственным значением.
|
|
|
§ 4. Уравнение с вырожденным ядром
4.1. Определение вырожденного ядра.
Def Ядро 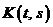 интегрального уравнения называется вырожденным, если его можно представить в виде конечной суммы произведений двух функций, из которых одна зависит только от
интегрального уравнения называется вырожденным, если его можно представить в виде конечной суммы произведений двух функций, из которых одна зависит только от 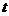 , а другая только от
, а другая только от 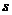 :
:
 .
.
4.2. Схема решения уравнения.
Рассмотрим интегральное уравнение Фредгольма II рода с вырожденным ядром 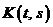 .
.

 (5)
(5)
 (6)
(6)
Заметим, что этот оператор конечномерен, т.к. образ действия оператора является линейной комбинацией конечного числа функций.
Очевидно, что решение интегрального уравнения с вырожденным ядром сводится к определению постоянных  (
(  ).
).
Если система не имеет решения, то, очевидно, интегральное уравнение также не имеет решения.
§ 5. Уравнения с симметричным ядром.
5.1. Характеристические числа интегрального уравнения.
Однородное интегральное уравнение Фредгольма II рода
(1) 
всегда имеет нулевое (тривиальное) решение  .
.
Те значения  (
(  ), при которых это уравнение имеет ненулевые решения называются характеристическими числами уравнения (1) или интегрального оператора
), при которых это уравнение имеет ненулевые решения называются характеристическими числами уравнения (1) или интегрального оператора  с ядром
с ядром 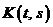 , а каждое ненулевое решение этого уравнения называется собственной функцией, соответствующей характеристическому числу
, а каждое ненулевое решение этого уравнения называется собственной функцией, соответствующей характеристическому числу  .
.
В случае произвольного ядра характеристические числа являются нулями определителя Фредгольма  , т.е. полюсами резольвенты
, т.е. полюсами резольвенты  . Отсюда, в частности, имеем, что уравнение Вольтерра характеристических чисел не имеет.
. Отсюда, в частности, имеем, что уравнение Вольтерра характеристических чисел не имеет.
Уравнение Вольтерра разрешимо  , т.е. характеристических чисел нет.
, т.е. характеристических чисел нет.
Если же ядро симметрично, то оператор имеет, по крайней мере, одно характеристическое число.
5.2. Общий вид решения интегрального уравнения с симметричным ядром.
Теорема 1. Если  в уравнении (1)не совпадает с характеристическими числами
в уравнении (1)не совпадает с характеристическими числами  ,
,  соответствующего однородного уравнения (2), то уравнение (1) имеет
соответствующего однородного уравнения (2), то уравнение (1) имеет  единственное непрерывное решение, определяемое формулой
единственное непрерывное решение, определяемое формулой  , где
, где  - ортонормированные собственные функции, соответствующие числам
- ортонормированные собственные функции, соответствующие числам  , а
, а  .
.
Теорема Гильберта-Шмидта.
В 
 ортонормированный базис из собственных векторов оператора
ортонормированный базис из собственных векторов оператора  . Если
. Если  - компактный самосопряженный оператор.
- компактный самосопряженный оператор.
Теорема 2. Если функция 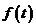 ортогональна всем собственным функциям
ортогональна всем собственным функциям  (
(  ) ядра
) ядра 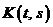 , то решением уравнения (1) будет сама функция
, то решением уравнения (1) будет сама функция 
 .
.
Теорема 3. Пусть  совпадает со значением
совпадает со значением  ранга
ранга  , т.е.
, т.е.  .
.
Тогда решение уравнения (1) существует  когда свободный член
когда свободный член  ортогонален всем собственным значениям, соответствующим числу
ортогонален всем собственным значениям, соответствующим числу  .
.
При этом (1) имеет  множество решений, которые содержат
множество решений, которые содержат  произвольных постоянных и даются формулой
произвольных постоянных и даются формулой
 , где
, где  - произвольные постоянные.
- произвольные постоянные.
Вывод. Очевидно, чтобы найти решение уравнения (1) достаточно знать характеристические числа и собственные функции оператора  .
.
5.3. Схема нахождения характеристических чисел и собственных функций.
На практике обычно сталкиваются со случаем, когда интегральное уравнение с симметрическим ядром является решением некоторой самосопряженной однородной краевой задачи для обыкновенного дифференциального уравнения.
В таких случаях нахождение характеристических чисел и собственных функций ядра (оператора) сводится к решению указанной краевой задачи.
Т.е. мы должны дважды продифференцировав наше интегральное уравнение составить некоторое дифференциальное уравнение, и найдя краевые значения  ,
,  ,
,  ,
,  составить краевые условия.
составить краевые условия.
Решается дифференциальное уравнение стандартно, используя общие решения.

§ 6. Уравнения типа свертки.
6.1 Уравнения Вольтерра.
Def Уравнением Вольтерра второго рода называется интегральное уравнение
 ,
,
где 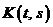 ограниченная измеримая функция
ограниченная измеримая функция  .
.
Поскольку это уравнение можно рассматривать как частный случай уравнения Фредгольма (с ядром, равным нулю при  ), теоремы Фредгольма справедливы и для уравнения Вольтерра.
), теоремы Фредгольма справедливы и для уравнения Вольтерра.
Однако для уравнений Вольтерра эти теоремы можно уточнить следующим образом.
Уравнение Вольтерра, при любой функции  имеет одно и только одно решение.
имеет одно и только одно решение.
6.2. Уравнение типа свертки.
Def Уравнением типа свертки называется интегральное уравнение Вольтерра II рода, ядро которого зависит лишь от разности аргументов

При этом функции  и
и 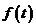 предполагаются непрерывными при
предполагаются непрерывными при  и возрастают не быстрее показательной функции, т.е.
и возрастают не быстрее показательной функции, т.е. 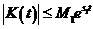 ,
, 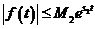 .
.
Решение уравнения типа свертки можно отыскать с помощью преобразования Лапласа.
§ 7. Преобразование Лапласа.
7.1. Определение функции-оригинала и изображения функции.
Def Функцией-оригиналом называется любая комплекснозначная функция  действительного аргумента
действительного аргумента 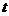 , удовлетворяющая условиям:
, удовлетворяющая условиям:
1)  интегрируема на любом конечном интервале оси
интегрируема на любом конечном интервале оси 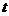 (локально интегрируемы);
(локально интегрируемы);
2) для всех отрицательных 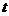

3)  с ростом
с ростом 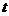 возрастает (по модулю) не быстрее показательной функции, т.е.
возрастает (по модулю) не быстрее показательной функции, т.е.  -ют такие постоянные
-ют такие постоянные 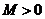 и
и 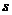 , что
, что 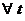
 .
.
Мы будем рассматривать непрерывные функции-оригинала.
Def Изображением функции  по Лапласу называется функция
по Лапласу называется функция  комплексной переменной
комплексной переменной  , определяемая равенством
, определяемая равенством
 .
.
То, что  есть изображение функции
есть изображение функции  , будем обозначать так
, будем обозначать так
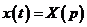 .
.
Функция  определена в полуплоскости
определена в полуплоскости  комплексной переменной
комплексной переменной  и является в этой полуплоскости аналитической функцией от
и является в этой полуплоскости аналитической функцией от 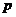 .
.
7.2. Свойства преобразования Лапласа.
1. Свойство линейности.
Для любых комплексных постоянных  и
и  выполнено
выполнено

2. Теорема подобия.
Для любого постоянного 
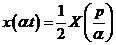 .
.
3. Дифференцирование оригинала.
Если функции  ,
,  ,…,
,…,  являются функциями-оригиналами и
являются функциями-оригиналами и 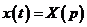 , то
, то  ,
,  .
.  , где под
, где под  понимается
понимается  ,
,  .
.
4. Дифференцирование изображения.
Дифференцирование изображения сводится к умножению на  оригинала
оригинала
 или вообще
или вообще  .
.
5. Интегрирование оригинала.
Интегрирование оригинала сводится к делению изображения на 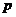 , т.е. если
, т.е. если 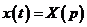 , то
, то  .
.
6. Интегрирование изображения
Если  сходится, то он служит изображением функции
сходится, то он служит изображением функции  :
: 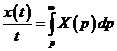 .
.
7. Теорема смещения
Если 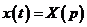 . То для любого комплексного
. То для любого комплексного 
 .
.
8. Теорема запаздывания. Если 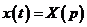 , то
, то 
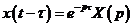 .
.
9. Теорема умножения (теорема о свертке).
Произведение двух изображений  и
и  , также является изображением, причем
, также является изображением, причем
 .
.
Интеграл в правой части называется сверткой функций  и
и 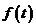 и обозначается символом
и обозначается символом  .
.
7.3. Таблица преобразования Лапласа.
Так как времени осваивать свойства преобразования у нас нет, то основные результаты вынесем в таблицу.

| 
| 
| 
| 
| 
|

| 
| 
| 
| 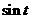
| 
|
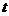
| 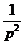
| 
| 
| 
| 
|

| 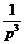
| 
| 
| 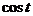
| 
|

| 
| 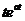
| 
| 
| 
|

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
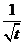
| 
| 
| 
| 
| 
|
§ 8. Решение уравнений типа свертки.
Пусть имеем интегральное уравнение Вольтерра II рода типа свертки
 .
.
Предположим, что функции 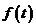 и
и  - оригиналы (т.е. удовлетворяющая условиям 1-3 из def).
- оригиналы (т.е. удовлетворяющая условиям 1-3 из def).
Можно показать, что в этом случае решение  также будет оригиналом и, следовательно, к обеим частям уравнения можно применить преобразование Лапласа. Полагая
также будет оригиналом и, следовательно, к обеим частям уравнения можно применить преобразование Лапласа. Полагая 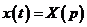 ,
,  ,
,  и используя теорему о свертке, согласно которой
и используя теорему о свертке, согласно которой  , получим
, получим  , получим
, получим  . Затем находим оригинал
. Затем находим оригинал  для
для  , который и будет решением интегрального уравнения.
, который и будет решением интегрального уравнения.
Заметим, что если  будет правильной рациональной дробью от
будет правильной рациональной дробью от 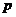 , то эту дробь надо разложить на сумму простых дробей и найти оригиналы для каждой простой дроби, используя свойства 1-9 или таблицу.
, то эту дробь надо разложить на сумму простых дробей и найти оригиналы для каждой простой дроби, используя свойства 1-9 или таблицу.
Дата добавления: 2018-04-05; просмотров: 847; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
