Тема 2. Мера и интеграл Лебега
Глава 1. Мера Лебега.
§ 1. Мера элементарных множеств.
Рассмотрим систему  множеств на плоскости
множеств на плоскости  , каждое из которых , определяется неравенствами
, каждое из которых , определяется неравенствами  ,
,  (знаки неравенств могут быть любыми, строгими, нестрогими)
(знаки неравенств могут быть любыми, строгими, нестрогими)
Множества из системы будем называть прямоугольниками.
Для каждого из прямоугольников определим его меру:
а) мера пустого множества равна 0 (  или
или 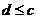 )
)
б) мера непустого прямоугольника (замкнутого, открытого или полуоткрытого) равна  .
.
Таким образом, каждому прямоугольнику  поставлено в соответствие число
поставлено в соответствие число  - его мера. При этом выполнены следующие условия
- его мера. При этом выполнены следующие условия
1)  действительна и неотрицательна
действительна и неотрицательна
2)  аддитивна, т.е., если
аддитивна, т.е., если  и
и  , то
, то  .
.
Мера  определена для прямоугольников, попробуем распространить меру на более широкий класс множеств с сохранением свойств 1 и 2.
определена для прямоугольников, попробуем распространить меру на более широкий класс множеств с сохранением свойств 1 и 2.
Def Плоское множество называется элементарным, если его можно представить в виде объединения конечного числа попарно непересекающихся прямоугольников.
Теорема 1. Объединение, пересечение, разность и симметрическая разность двух элементарных множеств также являются элементарными множествами, т.е. элементарные множества образуют кольцо.
Def Определим меру  для элементарных множеств следующим образом: если
для элементарных множеств следующим образом: если  , где
, где  -попарно непересекающиеся прямоугольники, то
-попарно непересекающиеся прямоугольники, то  . Причем
. Причем  не зависит от способа разложения в сумму конечного числа прямоугольников.
не зависит от способа разложения в сумму конечного числа прямоугольников.
Теорема 2. Если  - элементарное множество и
- элементарное множество и  конечная или счетная система элементарных множеств, такая, что
конечная или счетная система элементарных множеств, такая, что  , то
, то  .
.
|
|
|
Свойство меры  , устанавливаемое теоремой 2 (мера множества не превосходит суммы мер, покрывающих его множеств) называется полуаддитивностью.
, устанавливаемое теоремой 2 (мера множества не превосходит суммы мер, покрывающих его множеств) называется полуаддитивностью.
Из него вытекает свойство счетной аддитивности или  - аддитивности, состоящее в следующем
- аддитивности, состоящее в следующем
Если 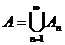 (
(  представлена в виде объединения счетного числа пересекающихся элементов множеств, то
представлена в виде объединения счетного числа пересекающихся элементов множеств, то 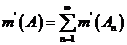 ).
).
§ 2. Лебегова мера плоских множеств.
2.1. Внешняя мера множеств.
Элементарные множества не исчерпывают всех множеств, встречающихся в анализе.
Def Внешней мерой множества  называется число
называется число  , где нижняя грань берется по всевозможным покрытиям множества
, где нижняя грань берется по всевозможным покрытиям множества  конечными или счетными системами прямоугольников.
конечными или счетными системами прямоугольников.
Теорема. Если  , где
, где  - конечная или счетная система множеств
- конечная или счетная система множеств  и
и  совпадают (замечание 1), то теорема 2 (§ 1) является частным случаем данной теоремы.
совпадают (замечание 1), то теорема 2 (§ 1) является частным случаем данной теоремы.
2.2. Измеримые множества.
Def: Множество  называется измеримым (в смысле Лебега), если
называется измеримым (в смысле Лебега), если 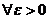 найдется такое элементарное множество
найдется такое элементарное множество 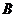 , что
, что  .
.
Def: Функция  рассматриваемая только на измеримых множествах называется лебеговой мерой и обозначается
рассматриваемая только на измеримых множествах называется лебеговой мерой и обозначается  .
.
Теорема 1. Сумма (объединение) и пересечение измеримых множеств есть измеримые множества.
|
|
|
Теорема 2. Если  - последовательность попарно непересекающихся измеримых множеств и
- последовательность попарно непересекающихся измеримых множеств и  , то
, то 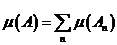 .
.
Теорема 2 устанавливает счетную аддитивность или  - аддитивность меры Лебега.
- аддитивность меры Лебега.
Из  - аддитивности вытекает еще одно свойство меры, называемое непрерывностью.
- аддитивности вытекает еще одно свойство меры, называемое непрерывностью.
Теорема 3 . если  - последовательность вложенных в друг друга измеримых множеств и
- последовательность вложенных в друг друга измеримых множеств и  , то
, то  .
.
2.3. Лебегова мера на прямой.
В этом параграфе излагалось построение меры Лебега для плоских множеств. Аналогично может быть построена Лебегова мера на прямой, в трехмерном пространстве или, вообще, в евклидовом пространстве любой размерности  . В каждом из этих случаев мера строится по одному и тому же образцу.
. В каждом из этих случаев мера строится по одному и тому же образцу.
Например на прямой. Определяем меру на простейших множествах: отрезки, интервалы, полуинтервалы:  ,
,  ,
, 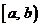 ,
, 
 .
.
§ 3. Лебегово продолжение меры.
3.1. Счетная аддитивность меры.
Плоская мера Лебега, построенная нами в §2  -аддитивна (теорема 2 из п.2.2.)
-аддитивна (теорема 2 из п.2.2.)
Def: Мера  называется счетно-аддитивной, или
называется счетно-аддитивной, или  -аддитивной, если для любых множеств
-аддитивной, если для любых множеств  , принадлежащих ее области определения (области определения меры) и удовлетворяющих условиям
, принадлежащих ее области определения (области определения меры) и удовлетворяющих условиям 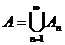 ,
,  имеет место равенство
имеет место равенство
 .
.
Лебегово продолжение меры.
Def: Непустая система множеств  называется кольцом, если из
называется кольцом, если из  .
.
|
|
|
Def Система множеств  называется полукольцом, если 1о из
называется полукольцом, если 1о из  .
.
2о. Если  и
и  , то
, то  можно представить в виде
можно представить в виде  , где
, где  -заданное и все
-заданное и все  .
.
Кроме того, предполагаем, что  (
(  т.к.
т.к.  ).
).
Задача о продолжении меры состоит в следующем. Каким образом, зная меру на узком классе множеств продолжить ее на более широкий класс множеств с сохранением свойств меры.
Def Мера  называется полной, если из
называется полной, если из 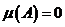 и
и  вытекает, что
вытекает, что 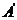 измеримо.
измеримо.
Глава 2. Измеримые функции
§ 1. Измеримые функции
11. Определение и основные свойства
Def Действительная функция  называется измеримой, если при любом действительном
называется измеримой, если при любом действительном  множество
множество  измеримо.
измеримо.
Теорема 1. Сумма, разность и произведение двух измеримых функций измеримы. Частное двух измеримых функций при условии, что знаменатель не обращается в нуль, тоже измеримо.
Теорема 2. предел сходящейся при каждом  последовательности измеримых функций измерим.
последовательности измеримых функций измерим.
1.2. Эквивалентные функции.
При изучении измеримых функций часто можно пренебречь их значениями на множестве меры нуль.
Def Две функции  и
и 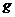 , заданные на одном и том же множестве
, заданные на одном и том же множестве 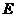 называются эквивалентными (обозначение
называются эквивалентными (обозначение  ), если
), если  .
.
Введем еще одно понятие
Def Говорят, что некоторое свойство выполнено почти всюду на 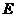 , если оно выполнено на
, если оно выполнено на 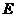 всюду, кроме, быть может, точек, образующих множество меры нуль.
всюду, кроме, быть может, точек, образующих множество меры нуль.
|
|
|
Теорема. Пусть функции  и
и 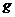 определены на некотором измеримом множестве
определены на некотором измеримом множестве 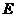 . Если функция
. Если функция  измерима и
измерима и  эквивалентна
эквивалентна 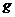 (
(  ), то
), то 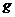 тоже измеримая функция.
тоже измеримая функция.
§ 2. Сходимость почти всюду
2.1. Определение сходимости почти всюду.
Def Последовательность  функций, определенных на некотором пространстве
функций, определенных на некотором пространстве 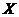 с заданной на нем мерой
с заданной на нем мерой  , называется сходящейся почти всюду к функции
, называется сходящейся почти всюду к функции  , если
, если 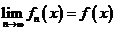 для почти всех
для почти всех  , т.е.
, т.е.  .
.
Теорема 1. Если последовательность измеримых функций  сходится к функции
сходится к функции  почти всюду на
почти всюду на 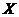 , то
, то  также измерима.
также измерима.
2.2. Теорема Егорова.
Теорема Егорова устанавливает связь между сходимостью почти всюду и равномерной сходимостью.
Теорема Егорова
Пусть 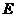 - множество конечной меры. Последовательность измеримых функций
- множество конечной меры. Последовательность измеримых функций 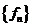 сходится на
сходится на 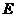 почти всюду к
почти всюду к  . Тогда
. Тогда 
 такое измеримое множество
такое измеримое множество  , что
, что
1) 
2) на 
 (равномерно)
(равномерно)
На множестве конечной меры сходимость почти всюду влечет за собой почти равномерную сходимость.
§ 3. Сходимость по мере
3.1. Определение сходимости по мере.
Def Говорят, что последовательность измеримых функций  сходится по мере к функции
сходится по мере к функции  , если для любого
, если для любого 
 .
.
Обозначают  .
.
Следующая теорема устанавливает единственность предела по мере.
Теорема
Если  и
и  , то
, то  (по мере
(по мере  )
)
3.2 Связь между сходимостью почти всюду и по мере.
Следующие две теоремы устанавливают связь между понятиями сходимости почти всюду и равномерной сходимости по мере.
Теорема 1 (Лебега). Если последовательность измеримых функций 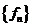 сходится почти всюду к некоторой функции
сходится почти всюду к некоторой функции  , то она сходится к ней по мере.
, то она сходится к ней по мере.
Однако в обратную сторону теорема не верна. Однако справедлива следующая теорема
Теорема 2 (Рисса)
Пусть последовательность измеримых функций  сходится по мере к
сходится по мере к  . Тогда из этой последовательности можно выбрать подпоследовательность
. Тогда из этой последовательности можно выбрать подпоследовательность  , сходящуюся к
, сходящуюся к  почти всюду.
почти всюду.
 .
.
3.3. Теорема Лузина и С-свойство
Мы определяли измеримые функции на произвольных множествах м в общем случае это понятие никак не связано с понятием непрерывной функции.
Теорема (Лузина)
Для того, чтобы функция  , заданная на отрезке
, заданная на отрезке  , была измерима, необходимо и достаточно, чтобы
, была измерима, необходимо и достаточно, чтобы 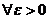
 такая непрерывная на
такая непрерывная на  функция
функция  , что
, что  .
.
Глава 3. Интеграл Лебега.
§ 1. Интеграл Лебега для простых функций.
1.1. Отличие от интеграла Римана.
Понятие интеграла Римана можно применить или к непрерывным функциям или имеющим лишь конечное число точек разрыва.
Для измеримых функций, которые могут быть разрывны всюду, где они определены (а могут быть заданы на абстрактном множестве, где понятие непрерывности не имеет смысла), конструкция интеграла Римана не годится.
Для таких функций Лебег ввел другое понятие интеграла.
Если в интегральных суммах Римана точки 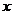 группируются по признаку близости их на оси
группируются по признаку близости их на оси  , то в интеграле Лебега они группируются по признаку близости значений функции в этих точках. Это сразу позволяет распространить понятие интеграла на очень широкий класс функций.
, то в интеграле Лебега они группируются по признаку близости значений функции в этих точках. Это сразу позволяет распространить понятие интеграла на очень широкий класс функций.
Кроме того, интеграл Римана вводится сначала для функций одной переменной, а затем уже переносится на случай нескольких переменных.
Интеграл Лебега определяется совершенно одинаково для функций, заданных на любых пространствах с мерой.
Заметим, что на абстрактных пространствах интеграл Римана вообще не имеет смысла.
Сначала определим интеграл Лебега для простых функций, а затем распространим на более широкий класс функций.
1.2. Простые функции
Def Простой называется измеримая функция, принимающая не более чем счетное число значений.
Теорема 1. Функция  , принимающая не более чем счетное число значений
, принимающая не более чем счетное число значений  измерима тогда и только тогда, когда все множества
измерима тогда и только тогда, когда все множества  измеримы.
измеримы.
Теорема 2. Для измеримости функции  необходимо и достаточно, чтобы она могла быть представлена в виде предела равномерно сходящейся последовательности простых функций.
необходимо и достаточно, чтобы она могла быть представлена в виде предела равномерно сходящейся последовательности простых функций.
1.3. Интеграл Лебега от простых функций.
Пусть  некоторая простая функция, принимающая значения
некоторая простая функция, принимающая значения 
 и пусть
и пусть  некоторое измеримое подмножество
некоторое измеримое подмножество 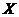 .
.
Определим интеграл от функции  по множеству
по множеству  равенством
равенством
(1)  , где
, где  если ряд справа сходится.
если ряд справа сходится.
Def Простая функция  называется интегрируемой или суммируемой (по мере
называется интегрируемой или суммируемой (по мере  ) на множестве
) на множестве  , если ряд (1) абсолютно сходится.
, если ряд (1) абсолютно сходится.
Если  интегрируема, то сумма ряда (1) называется интегралом от
интегрируема, то сумма ряда (1) называется интегралом от  по множеству
по множеству  .
.
1.4. Свойства интеграла Лебега от простых функций.
Установим некоторые свойства интеграла Лебега от простых функций.
1о 
2о 

3о Ограниченная на множестве  простая функция
простая функция  интегрируема на
интегрируема на  , причем, если
, причем, если  на
на  , то
, то  .
.
§ 2. Общее определение интеграла Лебега.
2.1. Определение суммируемой функции.
Def Функция  называется суммируемой (интегрируемой) на множестве
называется суммируемой (интегрируемой) на множестве  , если существует последовательность простых интегрируемых функций
, если существует последовательность простых интегрируемых функций 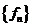 , сходящихся равномерно к
, сходящихся равномерно к  .
.
Предел 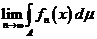 обозначим
обозначим  и назовем интегралом функции
и назовем интегралом функции  по множеству
по множеству  .
.
Таким образом, построение интеграла Лебега разбивается на два этапа.
Первый: непосредственное определение интеграла как суммы ряда для класса простых суммируемых функций, достаточно простого.
Второй: Распространение определения интеграла на более широкий класс с помощью предельного перехода.
Заметим, что сочетание двух этапов, подобных этим, присутствует при любом построении интеграла.
2.2. Свойства интеграла Лебега.
1о.  следует непосредственно из определения интеграла от простой функции (как сумма)
следует непосредственно из определения интеграла от простой функции (как сумма)
2о 
 причем из существования интеграла справа следует существования интеграла слева.
причем из существования интеграла справа следует существования интеграла слева.
3о Аддитивность  .
.
причем из существования интегралов справа следует существования интеграла слева.
4о Ограниченная на множестве  функция
функция  интегрируема на
интегрируема на 
5о Монотонность: если  на
на  , то
, то  .
.
Для простых функций следует из определения интеграла, а в общем случае с помощью предельного перехода.
5оо Из 5о следует: если  на
на  , то
, то 
5оо Если  для всех или почти всех
для всех или почти всех  , то
, то  .
.
6о Если 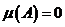 , то
, то 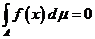 . Следует из определения интеграла.
. Следует из определения интеграла.
6оо Если  , то
, то  . Следует из определения интеграла.
. Следует из определения интеграла.
7о Если функция  интегрируема на
интегрируема на  и почти всюду
и почти всюду  , то
, то  также интегрируема на
также интегрируема на  .
.
8о Интегралы  и
и  существуют или не существуют одновременно.
существуют или не существуют одновременно.
2.3. Абсолютная непрерывность интеграла Лебега.
Свойство 6о из предыдущего пункта говорит, что интеграл Лебега по ножеству нулевой меры равен нулю для любой функции  .
.
Теорема. Пусть  интегрируема на
интегрируема на  . Тогда
. Тогда  такое, что для всякого измеримого
такое, что для всякого измеримого  такого, что
такого, что  следует
следует  .
.
§ 3.Предельный переход под знаком интеграла.
Вопрос о предельный переход под знаком интеграла, или, что то же самое, о почленном интегрировании сходящегося ряда, часто возникает в различных задачах.
В мат.анализе устанавливается, что достаточным условием такого предельного перехода является равномерная сходимость соответствующего ряда или последовательности.
Так как интеграл Лебега является обобщением интеграла Римана, то и следующие теоремы являются обобщением приведенного факта.
3.1. Теорема Лебега
Теорема (Лебега об ограниченной сходимости).
Пусть последовательность 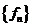 суммируемых функций 1) сходится по мере к функции
суммируемых функций 1) сходится по мере к функции  и 2)
и 2)  такая суммируемая функция
такая суммируемая функция  , что
, что 

Тогда функция  суммируема и
суммируема и 
Здесь  называется суммируемой мапсорантой последовательности
называется суммируемой мапсорантой последовательности 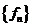 .
.
3.2. Теорема Бенно Леви
Теорема. Пусть на множестве 
 . Причем функции
. Причем функции  интегрируемы и их интегралы ограничены в совокупности
интегрируемы и их интегралы ограничены в совокупности
 .
.
Тогда почти всюду на  существует конечный предел
существует конечный предел  , и функция
, и функция  интегрируема на
интегрируема на  , причем
, причем  .
.
При этом на множестве, на котором предел 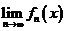 не существует, функцию
не существует, функцию  можно задать произвольно. Например, нулем
можно задать произвольно. Например, нулем  .
.
Следствие (Для ряда) если  и
и  , то почти всюду на
, то почти всюду на  ряд
ряд  сходится и
сходится и 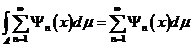 .
.
3.3 Теорема Фату.
Теорема. Если последовательность неотрицательных измеримых  сходится почти всюду на
сходится почти всюду на  к
к  , то
, то  .
.
§ 4. Сравнение интегралов Лебега и Римана.
Для простоты изложения рассмотрим связь между интегралами в одномерном случае.
4.1. Сравнение интегралов по отрезку.
Теорема. Если функция  интегрируема по Риману, то она интегрируема и по Лебегу и
интегрируема по Риману, то она интегрируема и по Лебегу и
 .
.
В обратную сторону теорема не верна. Например, функция Дирихле  на
на  интегрируема по Лебегу, но не интегрируема По Риману.
интегрируема по Лебегу, но не интегрируема По Риману.
4.2. Случай неограниченной функции.
Неограниченные функции вообще не могут быть интегрируемы по Риману, но многие из них интегрируемы по Лебегу.
Вначале определим интеграл Лебега от неограниченной неотрицательной измеримой функции  на множестве
на множестве  .
.
Построим вспомогательную функцию

Эта функция измерима и ограничена (числами). Теперь интеграл Лебега определяется как  .
.
Указанный предел всегда существует. Если он конечен, функцию называют суммируемой на  , если бесконечен – то не суммируемой.
, если бесконечен – то не суммируемой.
Теперь определим интеграл от знакопеременной неограниченной измеримой функции  на
на  с помощью равенства
с помощью равенства
 , где
, где


Def Функция  называется суммируемой, если
называется суммируемой, если  и
и  суммируемы, функция несуммируема, если хотя бы одна из неотрицательных функций
суммируемы, функция несуммируема, если хотя бы одна из неотрицательных функций  и
и  несуммируема.
несуммируема.
Из последнего определения легко вывести теорему
Теорема 1. Для суммируемости измеримой функции необходимо и достаточно, чтобы была суммируема функция  .
.
(Действительно, ведь  )
)
Из этой теоремы выводится следующая.
Теорема 2. Для абсолютной сходимости несобственного интеграла Римана необходимо и достаточно, чтобы  была суммируема, и тогда выполнено равенство
была суммируема, и тогда выполнено равенство
 .
.
Кроме того, справедливо равенство
 .
.
Следствие. Таким образом, из условной сходимости несобственного интеграла  следует несуммируемость функции
следует несуммируемость функции 
4.3. Случай неограниченного промежутка.
Заметим, что в этом случае справедлив аналог теоремы 2 из предыдущего пункта.
Теорема. Для абсолютной сходимости несобственного интеграла  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  была суммируема на
была суммируема на  . При этом выполнено равенство
. При этом выполнено равенство
 .
.
Заметим, что кроме того, справедливо равенство  .
.
§ 5. Пространства суммируемых функций.
Один из важнейших классов нормированных пространств составляют пространства суммируемых функций, в первую очередь пространство всех суммируемых функций  и пространство
и пространство 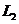 функций, суммируемых с квадратом.
функций, суммируемых с квадратом.
5.1. Пространство  .
.
Пусть 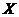 некоторое пространство с мерой
некоторое пространство с мерой  , будем считать меру
, будем считать меру  полной (т.е. любое подмножество любого множества меру нуль измеримо). Рассмотрим совокупность всех функций
полной (т.е. любое подмножество любого множества меру нуль измеримо). Рассмотрим совокупность всех функций  , суммируемых на
, суммируемых на 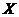 . Поскольку линейная комбинация суммируемых функций суммируема, то эта совокупность образует линейное пространство. Это пространство мы обозначим
. Поскольку линейная комбинация суммируемых функций суммируема, то эта совокупность образует линейное пространство. Это пространство мы обозначим  или, короче, просто
или, короче, просто  .
.
Введем в  норму
норму  . Легко проверить, что
. Легко проверить, что  удовлетворяет всем условиям нормы, за исключением одного, что
удовлетворяет всем условиям нормы, за исключением одного, что  .
.
Чтобы устранить эти расхождения элементами пространства  будем считать классы эквивалентных между собой суммируемых функций. (Иначе такой функционал называется полунормой).
будем считать классы эквивалентных между собой суммируемых функций. (Иначе такой функционал называется полунормой).
В  , как и во всяком нормированном пространстве, с помощью формулы
, как и во всяком нормированном пространстве, с помощью формулы  вводится расстояние. Сходимость последовательности суммируемых функций в смысле этого расстояния называют сходимостью в среднем.
вводится расстояние. Сходимость последовательности суммируемых функций в смысле этого расстояния называют сходимостью в среднем.
Весьма важным для многих вопросов тот факт, что пространство  полно, т.е. любая фундаментальная последовательность сходится.
полно, т.е. любая фундаментальная последовательность сходится.
Мера, имеющая счетный базис, называется сепарабельной мерой.
Теорема. Если мера  - сепарабельная мера на измеримом пространстве
- сепарабельная мера на измеримом пространстве 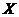 , то пространство
, то пространство  сепарабельно.
сепарабельно.
В частном случае, когда 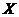 - отрезок числовой прямой, а
- отрезок числовой прямой, а  - мера Лебега, счетное всюду плотное множество в
- мера Лебега, счетное всюду плотное множество в  можно получить, взяв множество всех многочленов с рациональными коэффициентами.
можно получить, взяв множество всех многочленов с рациональными коэффициентами.
Вывод. Пространство  представляет собой полное нормированное (т.е. банахово) линейное пространство. Однако оно не является гильбертовым, т.к. определенную в нем норму нельзя задать с помощью скалярного произведения. А именно, не выполнено равенство параллелограмма
представляет собой полное нормированное (т.е. банахово) линейное пространство. Однако оно не является гильбертовым, т.к. определенную в нем норму нельзя задать с помощью скалярного произведения. А именно, не выполнено равенство параллелограмма  например для функций
например для функций  и
и  на
на  .
.
5.2. Пространство 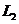 .
.
Определение. Функция  называется функцией, суммируемой с квадратом, если
называется функцией, суммируемой с квадратом, если 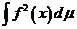 (конечен, существует).
(конечен, существует).
Совокупность всех таких функций мы обозначим  или
или 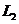 .
.
Заметим, что, как и в случае  ;
; 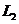 - линейное пространство, полное, сепарабельное.
- линейное пространство, полное, сепарабельное.
В отличие от  в
в 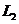 вводится скалярное произведение
вводится скалярное произведение
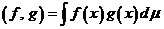 .
.
Поэтому 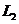 - гильбертово пространство.
- гильбертово пространство.
Норма в 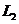 определяется формулой
определяется формулой  , а расстояние между элементами
, а расстояние между элементами  и
и 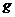
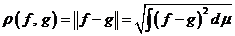 .
.
Сходимость функциональной последовательности по метрике пространства 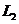 называется сходимостью в среднем квадратичном.
называется сходимостью в среднем квадратичном.
Теорема .Из сходимости в среднем квадратичном следует сходимость в среднем
Замечание. Обратная теорема не верна.
5.3. Соотношения между различными видами сходимости.
5.4. Пространство 
По аналогии с пространством 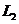 .
.
Def Измеримая функция  называется суммируемой с р-й степенью, если
называется суммируемой с р-й степенью, если  здесь
здесь  .
.
Совокупность всех таких функций обозначается  или
или  .
.
Теорема. Пространство  при любом
при любом  линейно, полно.
линейно, полно.
Введем норму в 
 .
.
Теперь  полное нормированное, т.е. банахово пространство.
полное нормированное, т.е. банахово пространство.
Пространство  сепарабельно, если мера
сепарабельно, если мера  на
на 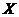 сепарабельна.
сепарабельна.
Дата добавления: 2018-04-05; просмотров: 1350; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
