Рис2. Графическая зависимость изменения численности популяций. Фазовый портрет системы

Математическое моделирование.

Моделирование – это исследование явлений и процессов на моделях. Построение модели связано с упрощением изучаемого процесса, в то же время модель должна отражать основные свойства оригинала.

В биологии и медицине используют четыре типа моделей:

1).Биологические. На них изучают общие биологические закономерности, патологические процессы, методы лечения и т.д. (Эксперименты на лабораторных животных).

2).Физические, которые ведут себя аналогично оригиналу. (Аппараты искусственного дыхания, кровообращения и т.д.).

3).Кибернетические – это различные электронные устройства, с помощью которых моделируются информационные процессы в живом организме.( Управление движением руки, ноги, искусственный интеллект и т.д.).

4).Математические. Моделируется математическая зависимость, которая описывает данный процесс. Позволяет

- уменьшить время исследования и число экспериментов;

- давать прогноз течения болезни и подобрать оптимальные варианты лечения;

- судить о таких системах и в таких условиях, которые сложно создать в эксперименте или клинике.

При построенииматематической модели различают 3 этапа:

1). Изучение процесса или явления, сбор данных о его параметрах и создание описательной теории, в которой выявляются причинно-следственные связи, существенные и несущественные детали процесса.

2). Составление математических (чаще всего дифференциальныхуравнений).

3). Рассмотрение на модели возможных результатов и выявление наиболее вероятного исхода, т.е. анализ решения уравнений.

При моделировании сложного процесса приходится составлять систему из большого числа дифференциальных уравнений, которые содержат большое число параметров. Для решения уравнений и определения параметров используют ЭВМ.

Основные направления математического моделирования:

1. Модели проницаемости клеточных мембран (нервная проводимость).

2. Иммунология и эндокринология (ход болезни и лечебные мероприятия).

3. Эпидемиология – распространение инфекционных болезней.

4. Процессы транспорта электронов.

5. Моделирование процесса старения клеток, злокачественных образований.

Математическое моделирование биологических процессов началось с создания первых простейших моделей экологической системы.

Попытки математического моделирования динамики, как отдельных биологических популяций, так и сообществ, включающих взаимодействующие популяции различных видов, предпринимались давно. Одна из первых моделей роста изолированной популяции была предложена ещё в 1798 году Томасом Мальтусом:

Данная модель задаётся следующими параметрами:

N – численность популяции;

μ – разность между коэффициентами рождаемости и смертности.

Модель совместного сосуществования двух биологических видов (популяций) типа «хищник-жертва» впервые была получена американским математиком Альфредом Лоткой в 1925 году. В 1926 году (независимо от Лотки) аналогичные (и более сложные модели) были разработаны итальянским математиком Вито Вольтеррой. Его глубокие исследования в области экологических проблем создали основу математической теории биологических сообществ ( математической экологии).

Поэтому эта классическая математическая модель («хищник-жертва») известна как модель « Лотки-Вольтерра».

Модель Лотки-Вольтерра (хищник-жертва).

Допустим, в некотором замкнутом районе живут рыси и зайцы. Рыси питаются только зайцами, а зайцы - растительной пищей, имеющейся в неограниченном количестве. Необходимо найти макроскопические характеристики, описывающие популяции. Такими характеристиками являются число особей в популяциях - число зайцев N₁ и число рысей N₂.

Запишем дифференциальные уравнения, описывающие процесс изменения числа особей во времени.

При отсутствии рысей, изменение числа зайцев будет:

α - коэффициент, характеризующий размножение зайцев (жертв).

При отсутствии зайцев, изменение числа рысей будет:

β - коэффициент, характеризующий вымирание рысей (хищников).

При совместном существовании зайцев и рысей:

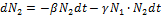
- коэффициент, характеризующий убыль зайцев, вследствие их встреч с рысями.

- коэффициент, характеризующий прирост рысей, вследствие их встреч с зайцами.

Скорость изменения популяций

(1)

Т.е. имеем систему нелинейных дифференциальных уравнений. В стационарном состоянии, когда не изменяется численность зайцев и рысей имеем:

и и, следовательно,

Т.е.

Решение этих уравнений (особые точки):

(2)

Отсюда следует:

Вывод1:стационарные состояния не зависят от численности популяции, а определяются только коэффициентами прироста и потерь для другого вида.

Для определения устойчивости в стационарных состояниях необходимо исследовать систему вблизи этих состояний.

Допустим, возникли некоторые случайные отклонения, флуктуации n₁, и n_г. Определим поведение системы.

Возьмем производные. С учетом того, что производная от стационарного состояния равна 0, получим:

Подставив в (1), раскроем скобки, приведем подобные члены и пренебрежем членами и вследствие их предполагаемой малости. Результатом пренебрежения ими будет линеаризация уравнений. В результате всех преобразований, окончательно получаем систему линейных дифференциальных уравнений второго порядка типа , описывающих консервативную колебательную систему, (т.е. идеализированную систему, в которой запас энергии в процессе колебаний остается постоянным):

Решив эту систему уравнений получаем

где: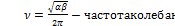

Вывод 2:популяции жертв и хищников испытывают периодические колебания одинаковой частоты , смещенные по фазе (причем максимум численности жертв всегда опережает максимум численности хищников).

Рис 1.Зависимость изменения популяций от времени.

Рассмотрим график зависимости N₁от N₂, т.е. избавимся от t.

Очевидно, что упрощенное решение нашей системы дифференциальных уравнений путем избавления от элементов и привело нас к тому, что модель пришлось стишком идеализировать, что плохо соответствует реальной модели.

Сделаем попытку решить систему дифференциальных уравнений (1) другим методом. Разделим одно уравнение на другое, тогда получим

Разделив переменные и проинтегрировав, получим решение:

Константу С можно найти в некоторый момент времени, когда мы знаем N₁ и N₂ ясно, что она может принимать множество значений.

Итак, мы получили выражение, связывающее две переменные и , т.е. зависимость =f ( )в неявном виде.

Начертим график этой функции. Полученная замкнутая кривая не является эллипсом (рис.2 ), хотя отдаленно и напоминает эллипс, который получается при сложении колебаний одинаковой частоты и произвольной фазы.

Рис2. Графическая зависимость изменения численности популяций. Фазовый портрет системы.

Однако и здесь имеют место следующие закономерности:

Вывод 3:

Колебания численности популяций,N₁ иN₂, действительно имеют место, они сдвинуты по фазе, но не являются гармоническими.

В экосистеме возникает то, что называется биоритмом.

В заключении приведем график, построенный на основании отчетов по отстрелу зайцев и рысей в Канаде в течении столетия. Видно, что основные выводы, полученные в упрощенной схеме «хищник-жертва», справедливы и для этой реальной ситуации.

Дата добавления: 2018-04-05; просмотров: 620; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!