Ангармонические колебания физического маятника
Лабораторная работа № 2.7 Свободные механические колебания Цель работы: изучение механических гармонических, ангармонических и затухающих колебаний с помощью математического и физического маятников. Приборы и принадлежности: физические маятники – шары на нитях, секундомер, линейка. Литература:[1, §§ 4,16-18,140-142,146], [2, Т.I, §§ 32,33,39,41,44,46, Т.III, §§ 123,124], [4, § 48-51,57-59], [5,6], [8],[18], [19], [21]. План работы: 1. Изучение гармонических колебанийфизического и математического маятников. 2. Изучение ангармонических колебанийфизического маятника. 3. Изучение затухающих колебаний. 4. Измерение периода малых колебаний математического маятника и определение ускорения свободного падения. 5. Исследование зависимости периода колебаний маятника от амплитуды. 6. Исследование затухающих колебаний маятника. 7. Изучение темы «Свободные колебания математического маятника» с помощью электронного учебника «Открытая физика».
Изучение гармонических колебаний математического и физического маятников
Различные механические колебания широко распространены в окружающем мире, в технике и быту. Простейшей моделью колебательной системы является математический маятник – подвешенное на тонкой нерастяжимой нити или на тонком стержне длиной  тело размером гораздо меньшим
тело размером гораздо меньшим  и потому принимаемое за материальную точку. Массы нити или стержня считаются пренебрежимо малыми по сравнению с массой тела
и потому принимаемое за материальную точку. Массы нити или стержня считаются пренебрежимо малыми по сравнению с массой тела  .
.
|
|
|
Физическим маятником называют твердое тело, которое может вращаться вокруг неподвижной горизонтальной осиО- оси вращения (качания) маятника, не проходящей через центр тяжести тела (рис. 9.1). Выберем направление оси  из плоскости колебаний вдоль оси вращения как показано на рис. 9.1, угол
из плоскости колебаний вдоль оси вращения как показано на рис. 9.1, угол  будем отсчитывать от вертикального положения покоящегося маятника в положительном направлении против часовой стрелки*1.
будем отсчитывать от вертикального положения покоящегося маятника в положительном направлении против часовой стрелки*1.


а б
Рис. 9.1. Отклонение физического маятника и вектор  вращающего момента при
вращающего момента при  ,
,  (а) и при
(а) и при  ,
,  (б); угол
(б); угол  отсчитывается от вертикали в положительном направлении против часовой стрелки
отсчитывается от вертикали в положительном направлении против часовой стрелки
Законом движения физического маятника является уравнение динамики вращательного движения твердого тела вокруг оси вращения 
 , (9.1)
, (9.1)
где I – момент инерции маятника относительно оси вращения,  - время,
- время,  – вращающий момент,
– вращающий момент,  - проекция момента на ось
- проекция момента на ось  ,
,  – сила тяжести, приложенная к центру массС и вызывающая повороты маятника, L – расстояние между осью вращения и центром масс маятника С,
– сила тяжести, приложенная к центру массС и вызывающая повороты маятника, L – расстояние между осью вращения и центром масс маятника С,  и
и  - вектор угловой скорости*2 и его проекция на ось
- вектор угловой скорости*2 и его проекция на ось  , вектор
, вектор  называют вектором углового ускорения. При выборе отсчета угла
называют вектором углового ускорения. При выборе отсчета угла  от вертикальной оси в положительном направлении против часовой стрелки (см. рис. 9.1)
от вертикальной оси в положительном направлении против часовой стрелки (см. рис. 9.1)
|
|
|
 . (9.2)
. (9.2)
Вектор угловой скорости и его проекция на ось  равны
равны
 ,
,  , (9.3)
, (9.3)
где  и
и  - вектор бесконечно малого поворота вокруг оси вращения*1 и его проекция на ось
- вектор бесконечно малого поворота вокруг оси вращения*1 и его проекция на ось  . Направление вектора угловой скорости
. Направление вектора угловой скорости  определяется по правилу буравчика с правой нарезкой (правого винта*2). Если расположить буравчик с правой нарезкой (правый винт) параллельно оси вращения и вращать его в ту же сторону, в какое вращается само тело, то направление ввинчивания буравчика (перемещения винта) укажет направление вектора
определяется по правилу буравчика с правой нарезкой (правого винта*2). Если расположить буравчик с правой нарезкой (правый винт) параллельно оси вращения и вращать его в ту же сторону, в какое вращается само тело, то направление ввинчивания буравчика (перемещения винта) укажет направление вектора  . При выборе отсчета угла
. При выборе отсчета угла  от вертикальной оси в положительном направлении против часовой стрелки (см. рис. 9.1)
от вертикальной оси в положительном направлении против часовой стрелки (см. рис. 9.1)
 . (9.4)
. (9.4)
Действительно, если вектор  направлен вдоль оси Oz , то поворот происходит против часовой стрелки, если смотреть на плоскость колебаний с конца оси Oz. При этом обе величины
направлен вдоль оси Oz , то поворот происходит против часовой стрелки, если смотреть на плоскость колебаний с конца оси Oz. При этом обе величины  и
и  имеют одинаковые знаки (положительные). Если же вектор
имеют одинаковые знаки (положительные). Если же вектор  направлен противоположно оси Oz , то поворот происходит в другую сторону – по часовой стрелке. При этом обе величины
направлен противоположно оси Oz , то поворот происходит в другую сторону – по часовой стрелке. При этом обе величины  и
и  снова имеют одинаковые знаки (отрицательные). С учетом формул (9.2) и (9.4) уравнение (9.1) запишется в виде
снова имеют одинаковые знаки (отрицательные). С учетом формул (9.2) и (9.4) уравнение (9.1) запишется в виде
|
|
|
 . (9.5)
. (9.5)
Противоположный выбор направления оси Oz изменит знаки проекций векторов  и
и  :
:  ,
,  и вновь приведет к уравнению (9.5). При выборе отсчета угла
и вновь приведет к уравнению (9.5). При выборе отсчета угла  от вертикальной оси в положительном направлении по часовой стрелке и прежнем (как на рис. 9.1) направлении оси Oz окажется
от вертикальной оси в положительном направлении по часовой стрелке и прежнем (как на рис. 9.1) направлении оси Oz окажется  ,
,  и мы вновь получим уравнение (9.5). Таким образом, вид уравнения (9.5) не зависит от выбора направлений оси Oz и отсчета угла отклонения.
и мы вновь получим уравнение (9.5). Таким образом, вид уравнения (9.5) не зависит от выбора направлений оси Oz и отсчета угла отклонения.
При малых отклонениях маятника из положения равновесия  и
и  . Вращающий момент
. Вращающий момент  , стремящийся вернуть маятник в положение равновесия, пропорционален углу отклонения
, стремящийся вернуть маятник в положение равновесия, пропорционален углу отклонения  и в этом отношении аналогичен упругой силе. Тогда уравнение (9.5) примет вид
и в этом отношении аналогичен упругой силе. Тогда уравнение (9.5) примет вид
 ,
,  , (9.6)
, (9.6)
а его решение является уравнением гармонических колебаний
 , (9.7)
, (9.7)
с амплитудой  , циклической частотой
, циклической частотой 
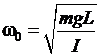 , (9.8)
, (9.8)
и периодом
 . (9.9)
. (9.9)
Математический маятник, подвешенный на тонком стержне (нити), является частным случаем физического маятника с  и моментом инерции
и моментом инерции 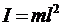 . В этом случае формулы (9.8), (9.9) переходят в формулы
. В этом случае формулы (9.8), (9.9) переходят в формулы
|
|
|
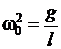 , (9.10)
, (9.10)
 . (9.11)
. (9.11)
Формула (9.11) позволяет определять ускорение свободного падения  по измерениям периода колебаний маятника
по измерениям периода колебаний маятника  :
:
 . (9.12)
. (9.12)
Формула (9.9) позволяет определять момент инерции  или его отношение к массе
или его отношение к массе  по измерениям периода колебаний маятника
по измерениям периода колебаний маятника  :
:
 . (9.13)
. (9.13)
Кинетическая энергия физического маятника в ходе его колебаний меняется по закону
 , (9.14)
, (9.14)
где  – угловая скорость. За нулевое значение потенциальной энергии маятника
– угловая скорость. За нулевое значение потенциальной энергии маятника  примем его потенциальную энергию при нулевом отклонении
примем его потенциальную энергию при нулевом отклонении  . Высота
. Высота  подъема центра масс тела с учетом приближенной формулы
подъема центра масс тела с учетом приближенной формулы  при
при  равна
равна
 . (9.15)
. (9.15)
Потенциальная энергия маятника равна
 . (9.16)
. (9.16)
В предыдущих рассуждениях предполагалось отсутствие трения, в таком случае в ходе колебаний по закону (9.7) полная механическая энергия физического маятника сохраняется
 . (9.17)
. (9.17)
Физические маятники №1 и №2, применяемые в настоящей работе, представляет собой сплошные однородные шары на нити длиной  . Пренебрегая массой нити, можно считать, что центр масс маятника находится в центре шара. Расстояние L от центра тяжести до точки подвеса равно
. Пренебрегая массой нити, можно считать, что центр масс маятника находится в центре шара. Расстояние L от центра тяжести до точки подвеса равно  . Для однородного шара радиуса
. Для однородного шара радиуса  и массы
и массы  момент инерции
момент инерции 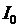 относительно оси, проходящей через его центр масс, равен
относительно оси, проходящей через его центр масс, равен
 . (9.18)
. (9.18)
Момент инерции  шара относительно оси, проходящей через точку подвеса, можно вычислить по теореме Гюйгенса*-Штейнера:
шара относительно оси, проходящей через точку подвеса, можно вычислить по теореме Гюйгенса*-Штейнера:
 . (9.19)
. (9.19)
Физический маятник №3, применяемый в настоящей работе, представляет собой тонкостенную сферу радиуса  (шарик для настольного тенниса) на нити длиной
(шарик для настольного тенниса) на нити длиной 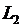 . Пренебрегая массой нити, можно считать, что центр масс маятника находится в центре шара. Расстояние L от центра тяжести до точки подвеса равно
. Пренебрегая массой нити, можно считать, что центр масс маятника находится в центре шара. Расстояние L от центра тяжести до точки подвеса равно  . Для тонкого кольца радиуса
. Для тонкого кольца радиуса  и массы
и массы  момент инерции
момент инерции 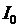 относительно оси, совпадающей с его диаметром равен
относительно оси, совпадающей с его диаметром равен
 . (9.20)
. (9.20)
Тонкостенную сферу радиуса  и массы
и массы  можно представить состоящей из множества колец и ее момент инерции
можно представить состоящей из множества колец и ее момент инерции 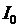 относительно оси, проходящей через центр масс, равен
относительно оси, проходящей через центр масс, равен
 . (9.21)
. (9.21)
Момент инерции  сферы относительно оси, проходящей через точку подвеса, можно вычислить по теореме Гюйгенса-Штейнера:
сферы относительно оси, проходящей через точку подвеса, можно вычислить по теореме Гюйгенса-Штейнера:
 . (9.22)
. (9.22)
В приближении  моменты инерции (9.19) и (9.22) равны
моменты инерции (9.19) и (9.22) равны 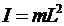 , и данные физические маятники можно считать математическими.
, и данные физические маятники можно считать математическими.
Ангармонические колебания физического маятника
Для изучения незатухающих ангармонических колебаний физического маятника удобно использовать закон сохранения энергии. Полная энергия маятникаЕ складывается из кинетической энергии 
 , (9.23)
, (9.23)
и потенциальной энергии 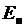
 . (9.24)
. (9.24)
Тогда полная энергия маятникаЕ
 . (9.25)
. (9.25)
Выразим угловую скорость  через угол
через угол 
 , (9.26)
, (9.26)
где
 ,
,  . (9.27)
. (9.27)
Отсюда
 . (9.28)
. (9.28)
При начальном отклонении маятника на угол  (при
(при  ) закон движения маятника буде иметь вид
) закон движения маятника буде иметь вид
 . (9.29)
. (9.29)
Период колебаний дается выражением
 . (9.30)
. (9.30)
Решение уравнения (9.30) записывается в виде
 , (9.31)
, (9.31)
где  – период малых гармонических колебаний, определяемый из (9.9).
– период малых гармонических колебаний, определяемый из (9.9).
Функция  называется полным эллиптическим интегралом первого рода.
называется полным эллиптическим интегралом первого рода.
 , (9.32)
, (9.32)
не выражается через элементарные функции и относится к так называемым специальным функциям математической физики. Ее значение для  вычисляется легко
вычисляется легко
 . (9.33)
. (9.33)
Для вычисления значений  при
при  на компьютере можно использовать математический пакет Maple [19] (см. рис. 9.2).
на компьютере можно использовать математический пакет Maple [19] (см. рис. 9.2).
Дата добавления: 2018-04-05; просмотров: 724; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
