Решение и анализ математической модели динамической системы

Разделив обе части приведенного выше дифференциального уравнения на I и обозначив

, , ,

получим дифференциальное, приведенное к стандартному виду

Решением таких уравнений является суперпозиция, т.е. сумма решений однородного дифференциального уравнения, соответствующего данному уравнению, и частного решения, т.е.

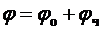где , — общее решение однородного уравнения и частное решение уравнения.

Однородное дифференциальное уравнение, соответствующее данному неоднородному, в рассматриваемом случае имеет вид

т.е. это, собственно, то же дифференциальное уравнение, но с нулевой правой частью. А это означает, что рассматриваемая динамическая система находится в невозмущенном состоянии, точнее, система выведена из состояния покоя и предоставлена сама себе.

Решением уравнения будет , где С — постоянная интегрирования, z — корень характеристического уравнения

Корни этого уравнения .

Тогда решение уравнения принимает вид

Из решения уравнения следует: при положительном n, с увеличением времени , т.е. , как функция времени, – затухающая. Это всегда имеет место для рассматриваемых динамических систем (всегда имеет место рассеяние энергии системой), каков бы ни был дискриминант (положительный или отрицательный).

На характер функции существенное влияние оказывает знак подкоренного выражения. В случае если , функция будет иметь вид кривой, плавно приближающейся к нулю.

Рассмотрим более подробно случай, когда выражение под корнем отрицательное, т.е. когда , или .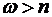

В этом случае поступают следующим образом. Выражение записывают в виде

, где , .

Тогда решение уравнения примет вид .

Функция - это полная гармоническая функция или функция Эйлера

Тогда решение уравнения примет вид

Постоянные интегрирования С₁ и С₂ определяются из начальных условий. Для дальнейшего анализа удобно решение уравнения свернуть и представить в виде

где — амплитуда, — частота, 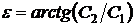—фаза.

Из полученного следует: решение уравнения — периодическая затухающая функция времени.

Физически это означает — динамическая система, выведенная из равновесного состояния или состояния покоя и предоставленная самая себе, колеблясь вокруг равновесного (исходного) состояния, с течением времени приходит к этому равновесному состоянию или состоянию покоя.

Величина p называется частотой собственных колебаний системы и зависит от массы, жесткости и демпфирующей способности системы.

Рассмотрим, с какими параметрами происходят колебания системы. В случае, если n значительно меньше ω, можем считать, что

— это частота собственных колебаний крутильного маятника, которая зависит от момента инерции и жесткости. Увеличение жесткости вала приводит к увеличению частоты, а увеличение момента инерции — к ее уменьшению.

Изменение демпфирующих свойств системы (рассеяния энергии) влияет как на частоту, так и на амплитуду колебаний. Увеличение потерь энергии приводит к уменьшению частоты собственных колебаний и к их затуханию — уменьшению амплитуды по логарифмической кривой . Скорость (интенсивность) убывания амплитуды обусловливается параметром

характеризующим рассеивающую (демпфирующую) способность системы. Поэтому параметр n называют логарифмическим декрементом колебания.

Таким образом, линейная динамическая система второго порядка, выведенная из равновесного состояния (равномерного движения или покоя) и предоставленная самая себе с течением времени, колеблясь, возвращается в исходное состояние. При этом скорость ее возвращения и колебания вокруг этого состояния обусловливаются параметрами самой системы – рассеивающей способностью, жесткостью и инерционными свойствами системы.

Частное решение дифференциального уравнения обычно ищут в том же виде, что и его правая часть, но на степень выше, если это линейная или криволинейная зависимость или в виде полной гармонической функции, если она задана неполной гармонической функцией.

Пусть правая часть уравнения (внешнее возмущение) задано периодической функцией вида

где Q — амплитуда, l — частота внешнего возмущения. Тогда

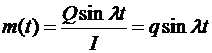, где .

Уравнение примет вид

Частное решение уравнения ищем в виде

Далее поступают следующим образом. Это решение подставляют в исходное уравнение и определяют неизвестные А и В таким образом, чтобы они удовлетворяли решению. Найдем первую и вторую производные

;

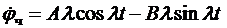После подстановки полученных производных в исходное уравнение, будем иметь

Собрав члены при sin λt и cos λt, получим систему двух алгебраических уравнений с двумя неизвестными А и В вида

которое однозначно решается относительно неизвестных.

Решение системы найдем в виде , , где

Получим

Преобразуем полученное выражение:

;

где — фаза вынужденных колебаний.

Рассмотрим физический смысл полученного решения, для чего запишем его в виде

Величина

соответствует деформации вала под действием статической нагрузки, равной амплитуде колебаний нагрузки Q.

Величину

называют коэффициентом динамичности системы.

Тогда частное решение уравнения примет вид

или .

Полное решение уравнения (математической модели):

Следует заметить, что при некотором t = T_п величина первого слагаемого — амплитуда собственных колебаний — становится близкой к нулю (после окончания так называемого переходного процесса) и для установившегося режима работы (t > T_п) решение математической модели примет вид

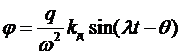Другими словами, в установившемся режиме работы колебания являются постоянными и проходят с частотой внешнего возмущения.

Рассмотрим, далее более подробно коэффициент динамичности системы. График зависимости k_д от частоты внешней нагрузки λ представлен на рис. 3.4. На графике можно выделить три зоны, поведение динамической системы в которых будет различным:

Зона 1 — 0 ≤ λ < λ₁, при этом k_д ≈ 1. Это означает, что при внешнем возмущении с этой частотой перемещения в системе равны перемещениям под действием такой же по величине статической нагрузки. Такие частоты иногда называют прошивными, нагрузка прошивает динамическую систему без изменения. Это так называемая низкочастотная составляющая нагрузки.

На рис. 3.5. представлены колебания системы при соотношении частот собственных и вынужденных колебаний λ/р = 1/10. На протяжении времени переходного процесса T_п на преобладающие вынужденные колебания с частотой λ накладываются затухающие собственные колебания с частотой р. По окончании переходного процесса колебания системы происходят с частотой внешнего возмущения и постоянной амплитудой, равной Q / C.

Зона 2 — λ₁ ≤ λ < λ₂, значение λ близко к частоте собственных колебаний системы. При этом значение k_д значительно превышает 1.

Значение k_д достигает максимума при частоте . Эта частота называется резонансной, а рассматриваемый диапазон частот — зоной резонанса.

На рис. 3.6 представлены колебания системы при λ = λ_р. В течение переходного процесса T_п происходит накопление энергии системой, и амплитуда колебаний возрастает, после чего происходят колебания с амплитудой, многократно превышающей амплитуду колебаний в зоне прошивных частот. Величина коэффициента динамичности при резонансе составляет

, или при ω >> n .

Зона 3 — λ > λ₂ , k_д уменьшается и при увеличении частоты стремится к нулю. Это высокочастотная составляющая нагрузки.

На рис. 3.7. представлены колебания системы при соотношении частот собственных и вынужденных колебаний λ/р = 5/1. Видно что наибольшая амплитуда колебаний имеет место во время переходного процесса. Амплитуда вынужденных колебаний в установившемся режиме весьма мала.

Подобие

Дата добавления: 2018-04-05; просмотров: 697; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!