Классификация событий. Действия над событиями
Теория вероятностей – математическая наука, изучающая закономерности, присущие массовым случайным явлениям. Предметом теории вероятностей являются математические модели случайных явлений. Под случайным явлением понимают явление, предсказать исход которого невозможно. Цель теории вероятностей – осуществление прогноза в области случайных явлений, влияние на ход этих явлений и их контроль.
Случайные события
Комбинаторика. Алгебра событий.
Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используют при непосредственном подсчете вероятностей.
Размещениями называют множества, составленные из n различных элементов по k элементов, которые отличаются либо составом элементов, либо их порядком. Число всех различных размещений определяется формулой:
.
Сочетаниями из n различных элементов по k называют множества, содержащие k элементов из числа n заданных, и которые отличаются хотя бы одним элементом. Количество различных сочетаний определяется формулой:
.
Перестановки. Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками. Количество различных перестановок n элементов определяется формулой:
.
Пример.
В урне 3 шара с номерами 1, 2, 3. Из урны один за другим извлекаются два шара. Определить число всех возможных пар шаров.
|
|
|
Решение.
Общее число пар равно числу размещений из трех элементов по два.
.
Этот результат можно получить и простым перебором. Перечислим возможные комбинации: (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2).
Пример.
В урне 3 шара с номерами 1, 2, 3. Из урны один за другим извлекаются три шара. Определить число всех возможных троек шаров.
Решение.
Число всех троек равно 
.
Или (1, 2,3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2,1).
Пример.
В урне 9 шаров с номерами 1, 2, … 9.
а) из урны один за другим извлекаются три шара. Номера записываются в порядке появления шаров. Определить число всех возможных вариантов получаемых трехзначных чисел;
б) из урны извлекаются три шара одновременно. Определить число всех возможных троек;
в) из урны один за другим извлекаются все шары. Определить число всех возможных вариантов получаемых девятизначных чисел.
Решение.
а) 
;
б) 
;
в) 
.
Задачи.
16.1Сколько элементарных исходов благоприятствует событию «на обоих кубиках выпало одинаковое число очков» при подбрасывании двух игральных кубиков?
16.2Подбрасывается два игральных кубика. Какому событию благоприятствует больше элементарных исходов: «сумма выпавших очков равна 7» или «сумма выпавших очков равна 8»?
|
|
|
16.3Сколькими различными способами можно выбрать три лица на три различные должности из десяти кандидатов?
16.4Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов?
16.5Сколькими различными способами могут разместиться на скамейке 5 человек?
16.6В урне 15 белых и 5 черных шаров. Из урны извлекаются 5 шаров. В полученной группе 2 белых шара. Определить число всех возможных вариантов появления такой группы шаров.
16.7Определить число всех вариантов размещения r шаров по n урнам.
16.8На 10 карточках записаны цифры 0, 1, 2, … 9. Берут 4 карточки и составляют из цифр, написанных на них, четырехзначное число. Сколько различных четырехзначных чисел можно составить таким образом?
16.9Сколько различных правильных дробей можно составить из чисел 3, 5, 7, 11, 13, 17, 19, 23 так, чтобы в каждую дробь входило два числа?
16.10Сколькими способами можно из 40 человек, поступающих в вуз, создать 4 группы специальностей по 10 человек в каждой?
16.11Сколько различных вариантов хоккейной команды можно составить из 9 нападающих, 5 защитников, 3 вратарей, если в состав команды должны войти 3 нападающих, 2 защитника и 1 вратарь?
Классификация событий. Действия над событиями.
|
|
|
Опытом или испытанием называют всякое осуществление комплекса условий или действий, при которых наблюдается соответствующее явление. Возможный результат опыта называют событием. Случайным называется событие А, которое в данном опыте может произойти, а может и не произойти. Достоверным называется событие W, которое обязательно произойдет в этом опыте. Событие Æ называется невозможным в данном опыте, если оно в этом опыте произойти не может. Два события называются совместными в данном опыте, если появление одного из них не исключает появления другого в этом опыте, и несовместными, если они не могут произойти вместе при одном и том же испытании. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из противоположных событий обозначено буквой А, то другое обозначают буквой 
. Например, если А – «попадание», то - «промах» при одном выстреле в мишень. Множество событий А1, А2, …, Аn называют полной группой, если они попарно несовместны, а появление одного (и только одного) из них является достоверным событием. Например, полную группу образуют события А1, А2, …, A6,где Ak (k = 1, 2, ..., 6) - событие «верхней оказалась грань с цифрой k»при подбрасывании игрального кубика.
|
|
|
Суммой или объединением двух событий называется событие, состоящее в появлении хотя бы одного из них. Сумма двух событий А и В обозначается через 
или 
.
Произведением или пересечением двух событий называется событие, состоящее в одновременном их появлении. Произведение двух событий А и В обозначается через 
или 
.
Определения вероятности.
Классическое определение вероятности.
События считают равновероятными (или равновозможными), если нет оснований полагать, что какое-либо событие имеет больший шанс появления. Вероятность события А определяется формулой:
,
где п - число равновероятных событий, образующих полную группу элементарных исходов W={w1,…,wn} для данного опыта, т - число тех элементарных исходов {wk|wkÌA}, которые благоприятствуют событию А. Множество W равновероятных исходов опыта, образующих полную группу, называют пространством элементарных событий (и используют для него то же обозначение, что и для достоверного события). Свойства вероятности события:
1) вероятность достоверного события равна единице: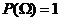 
;
2) вероятность невозможного события равна нулю: P(Æ) = 0;
3) вероятность любого события удовлетворяет неравенствам 
.
Дата добавления: 2018-04-04; просмотров: 970; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!