Методика обоснования исходной информации и построения развернутой экономико-математической модели

Приведенная экономико-математическая модель чаще всего используется для оптимизации распределения кормов на стойловый период. Хотя в равной мере может быть использована для расчетов по месяцам или другим периодам.

В качестве единиц измерения можно взять среднее за период поголовье, или количество кормодней. Во втором случае объем расчетов увеличивается, ибо рационы приходится считать в кг на кормодень.

Предельное поголовье животных за плановый период определяем по данным "движения животных". Минимальная и максимальная нормы скармливания кормов определяем по методике, изложенной ранее.

Ресурсы кормов (D_h) определяем согласно актов по оприходованию кормов или по остаткам этих кормов, если расчет ведем не на стойловый, а другой период.

Ограничения на кооперативные связи по кормам, т.е. 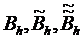принимаем в размере договоренностей.

Наиболее сложным является обоснование показателя d_ij. Он связан с продуктивностью животных и расходом питательных веществ на 1ц продукции.

Поскольку данная модель используется в расчетах на текущий год, то методика расчета d_ij та же, что и в главе 12, т.е. показателя A_i

Показатель k_ih т.е. содержание вещества i в корме h, целесообразно определить по данным химического анализа. Надо иметь в виду, что разрыв в питательности кормов достигает 2-х и больше раз.

Условия обмена кормов (коэффициент f_h) могут быть совершенно разными для данного хозяйства и других.

В процессе решения важно определить на каких условиях обмен выгоден.

Цены на корма и на продукцию следует брать текущие. При этом издержки по обмену кормов, как правило, несет предприятие — инициатор обмена.

Механизм использования кормов в реальной ситуации бывает более сложным, особенно в условиях перехода к рынку, когда кооперативные связи могут осуществляться по нескольким каналам и при различных финансовых условиях. Следует учитывать, что уже сейчас условия кооперации неодинаковы. Они отличаются в зависимости от финансового положения, обеспеченности животных кормами, устойчивости кооперативных связей.

В этих условиях изложенная выше базовая модель может иметь ряд дополнений. Эти дополнения связаны с тем, что покупка животных, молодняка, обмен кормов определяется в процессе решения задачи из числа нескольких возможных вариантов. Дополнения могут быть следующие.

Допустим, что в кооперативных связях участвуют п кооперирующихся предприятий (N₀ — множество кооперирующихся предприятий).

N₁ — множество предприятий, от которых получаем ресурсы (молодняк, корма);

N₂ — множество предприятий, которым отдаем ресурсы. При такой ситуации в левой и правой части соотношения по поголовью могут быть дополнения:

… + ∑ x_jn, j  J_0, n  N₁

где х_jn — поголовье молодняка вида, половозрастной группы j от предприятия п.

Аналогичным образом соответственно по балансу отдельных видов кормов.Вместо переменных  может стоять

 и т.д. .

При подобной ситуации возможны различные условия обмена. Ограничение по обмену будет иметь вид

Коэффициент f_hn предполагает, что по одному и тому же корму, но с различными предприятиями могут быть различные условия обмена.

В случае, если кооперация затрагивает несколько предприятий, то решив задачу мы определим, при каких из вариантов обмена, с точки зрения конечных результатов, обмен допустим.

При подобной записи имеется в виду, что издержки по кооперации, как и выручка от нее будут отличны и тогда в целевой функции следует учесть

При такой записи имеется в виду, что как выручка, так и издержки от обмена с каждым предприятием индивидуальны.

 

Пример:В соответствии со структурной моделью, ее соотношениями составляем развернутую модель (задачу).

Итак, согласно соотношению 1 ограничения по поголовью животных следующие.

1. Допустим, что в хозяйстве две половозрастные группы:

коровы и молодняк крупного рогатого скота;

x₁— поголовье коров, голов;

x₃+ x₂+ 35 ≤x₁≤40 + x₂ + x_3,

x₂ — покупка племенных животных, голов;

x₃— перевод из младшей группы, голов;

2. x₄— молодняк КРС,

x₄ = 0,95x₁ + x₅ + x₆,

— покупка молоднякапри первом и втором вариантах цен.

3. Ограничение на кооперативныесвязи

x₂≤2.

4. x₃≤6 — перевод молодняка из младшей группы в старшую.

5. x₅≤ 12 — объем возможной покупки при первом варианте цен.

6. x₆≤ 15 — возможные покупки при втором варианте цен.

7. При записи ограничения по балансу, например, концентратов учитываем продуктивность животных: надой, привес и в соответствии с ними потребность в отдельных кормах на голову за расчетный период

5х₁+3х₄+х₇+х₈≤300+х₉+х₁₀+х₁₁+х₁₂,

х₇, x₈ — скользящие переменные концентратам для коров и молодняка;

х₉, x₁₀— варианты покупки концентратов при двух вариантах цен;

х₁₁, x₁₂— варианты получения концентратов от обмена на сено;

5; 3 — минимальная норма расхода концентратов соответст­венно на одну корову и одну голову молодняка, ц;

8. По балансу сена, ц

8x₁ + 4x₄+ x₁₃ + x₁₄≤ 700 - x₁₅ - x_16,

x_{13, 14}— скользящие по сену для коров и молодняка;

x_{15, 16} — два варианта обмена сена на концентраты;

Скользящая переменная обозначает, как отмечено выше, добавку кормов на все поголовье

x₇≤ (8 - 5)x₁,

где 8 — максимальная норма скармливания корма.

Ограничения на покупные корма (х₉,х₁₀) на концентраты от обмена (х₁₁,х₁₂) и на сено в обмен (х₁₅,х₁₆) записываем, исходя из договоренностей или из своих возможностей.

Соотношения по условиям обмена.

Допустим, что первое предприятие дает концентраты (х₁₁) при условии — за 1ц концентратов 2ц сена, второе — акционерное предприятие или кооператив — дает концентраты (х₁₂) при условии, что за 1ц концентратов получит 4ц сена. Тогда имеем.

9. x₁₁=x₁₅ /2.

10.x₁₂=x₁₆ /4.

Ограничение по балансу питательных веществ включает потребность в этих веществах и их наличие с учетом перераспределения. При этом наличие питательных веществ определяется правой частью ограничений по балансу отдельных видов кормов.

Допустим, что в результате выполняемых расчетов на 1 голову взрослых животных требуется 20ц.к.ед., на голову молодняка — 11ц.к.ед.

20x₁ + llx₄≤ 1,1(300 + х₉ + х₁₀ + х₁₁ + х₁₂) +

+ 0,45(700 - х₁₅ -х₁₆).

При этом возможна ситуация, когда питательность кормов, полученных от обмена, различна. В этом случае коэффициенты питательности при соответствующих переменных будут разными.

Аналогичным образом записываем ограничения по другим веществам.

Соотношение 8 структурной экономико-математической модели, обеспечивает баланс питательных веществ по предприятию в целом. Подобный баланс не обеспечивает оптимизации рационов в разрезе половозрастных групп.

Чтобы устранить этот недостаток, т.е. оптимизировать рационы кормления в разрезе каждой половозрастной группы, записываем ограничения по содержанию питательных веществ в дополнительных кормах, обозначенных скользящими переменными. Смысл ограничения 9 состоит в том, что разница между потребностью животных в питательных веществах и содержанием этих веществ в рационе по минимальным нормам покрывается содержанием веществ в кормах, обозначенных скользящими переменными.

12. Расшифровывая соотношение 9, запишем ограничение по содержанию кормовых единиц в дополнительных кормах для коров

[20 - (5 • 1,1 + 8 • 0,45+...)] x₁≤ 1,1х₇+ 0,45x₁₃.

Возможна ситуация, когда предприятие (фермерское хозяйство, кооператив и т.д.) включилось в систему государственно-кооперативного распределения продукции, т.е. имеет договорные поставки, а остальную часть продукции реализует на рынке, промышленным предприятиям и т.д. Поэтому следует предусмотреть, как производство, так и распределение продукции.

13. Ограничения по производству и распределению продукции:

—по молоку

17x₁=x₂₀+x₂₁+x₂₂,

где х ₂₀— договорные поставки, который не превышает 80% объема производства (лучше 70%, в этом случае будут созданы товарные ресурсы для развития хозяйства).

14. 450≤x₂₀≤500.

15. 130 ≤X₂₁≤ 150, где X₂₁ — реализации молока крупным промышленным предприятиям и т.д.

16. Х₂₂ — реализации на рынке

200≤ Х₂₂≤400 .

17. Аналогично, как и ограничение 13, записываем ограничение по производству и распределению говядины и других видов продукции.

Тогда целевая функция — максимум прибыли будет иметь вид

Fmах = 500х₂₀ + 580x₂₁ + 700х₂₂ - 30х₉ - 42х₁₀ - З6х₁₁ - 38x₁₂ + 10x₁₅ + 10x₁₆ - 45х₅ • 50 - 80 • 50x₆,

где500 и т.д. коэффициенты, характеризующие сумму прибыли или затраты материально-денежных средств на единицу отрасли (продукции) при F_min .

Решив задачу, определим рационы кормления, распределение собственных кормов и самое главное — кооперативные связи по кормам, животным, а также целесообразные варианты реализации продукции и объемы реализации по потребителям. Получим информацию о том, до каких пределов увеличения цен на приобретаемые корма и животных выгодно поддерживать кооперативные связи.

В результате решения задачи мы получим значения скользящих переменных по кормам, на основе которых и минимальных норм скармливания определим значения оптимальных рационов по формуле

Например: минимальная норма скармливания концентратов на корову = 5ц, значение скользящей переменной — 84ц, поголовье коров —x_j = 40. Тогда расход концентратов на 1 корову по оптимальной программе использования кормов в хозяйстве составит 5 + 84 / 40 = 5 + 2,1 = 7,1ц.

По результатам решения определим, при каких ценах кооперативные связи выгодны.

Следует отметить, что существенное влияние на результаты решения задачи оказывает нестабильность производства кормов. Обеспеченность животных кормами колеблется по годам и существенно связана с природными факторами.

Обеспеченность животных кормами в неблагоприятные годы примерно на 17-22% ниже среднего уровня. Это предполагает нестабильность в обеспечении животных кормами и производстве продукции.

В условиях рынка такая ситуация может привести к невыполнению предприятием обязательств и к их разорению. Поэтому стабильность в обеспечении животных кормами является одной из важнейших предпосылок стабильности.

Перед предприятиями стоит задача обеспечить стабильность кормовых ресурсов. Это можно достигнуть, с одной стороны, уменьшением влияния природных факторов на результаты производства, с другой стороны, созданием стабилизационного фонда кормов.

Первый путь стабилизации требует значительных средств, времени на совершенствование технологии. Его следует осуществить, но в нынешних условиях предприятиям необходимо создать стабилизационный фонд кормов за счет ресурсов, полученных в благоприятные годы. Очевидно, этот фонд будет составлен из кормов, не требующих относительно больших издержек на хранение, т.е. транспортабельных: концентратов, травной муки, гранулированных кормов.

Максимальный объем использования данного фонда в неблагоприятные годы зависит от максимального числа неблагоприятных лет, которые следуют друг за другом (в наших условиях чаще всего из 10 лет 3 благоприятных, 4 неблагоприятных и 3 средних). Следовательно, при планировании программы использования кормов максимальный объем стабилизационного фонда, который может быть использован в данном году, будет составлять 50%.

 

Недостатком приведенной выше экономико-математической модели является заранее заданная продуктивность животных. Это сужает возможности модели, снижает гибкость и границы ее применения. Во избежание этого следует обеспечить формирование продуктивности в процессе решения задачи. С этой целью расчет потребности животного в кормах и питательных веществах производим в расчете на минимальную продуктивность.

Вводим дополнительные скользящие переменные по кормам, за счет которых возможно приращение продуктивности животных. В этом случае левая часть соотношения 2 структурной экономико-математической модели будет иметь вид

где 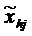 — скользящая переменная по корму h для вида, половозрастной группы j, для приращения продуктивности;

Левая часть соотношения 3 будет иметь вид

Введение новой скользящей переменной не должно нарушать физиологические требования животного к кормлению.

Изменится и содержание целевой функции. Потребуется ввести дополнительное соотношение

где H₄ — множество кормов, выделяемых для приращения продуктивности сверх минимального уровня, _; с_hj— стоимость дополнительной продукции от скармливания единицы корма h животным вида или половозрастной группы j.

В результате решения задачи определим как перечень, так и объем кормов, в рамках ресурсов хозяйства, которые целесообразно выделить отдельным видам и половозрастным группам животных для приращения их продуктивности.

 

---

Дата добавления: 2018-04-04; просмотров: 383; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!