Количественная оценка информации

⇐ ПредыдущаяСтр 3 из 17Следующая ⇒

При введении понятия энтропии мы исходили из количества событий, о которых нам необходимо получить информацию. Таким образом, энтропия характеризует количество информации, получаемой путем исследования интересующего нас процесса, если мы можем получить в свое распоряжение сведения о любом из М интересующих нас событий. Возможен, однако, такой исход исследования (или измерений), когда о некоторых событиях из рассматриваемых М событий сведения фактически не будут получены. Допустим, что до проведения исследований предусматривалась реализация одного из M₁ событий, а после проведения исследований выяснилось, что в данном случае могут быть реализованы лишь M₂ из предусмотренных ранее M₁ событий, но осталось невыясненным, какое именно из этих M₂ событий реализовано в действительности. Энтропия исследуемого процесса до проведения исследований могла достигать значения

а после проведения исследований уменьшилась до значения, не превышающего

В таком случае количество I полученной информации определяется разностью между исходной и конечной энтропиями:

I=H₁ – H₂ . (2.5)

Формула (2.5) дает обобщенную количественную оценку информации и соответствует формулировке: количество информации равно убыли энтропии. Величина исчерпывающей информации соответствует H₂=0и равна исходной энтропии.

В качестве примера рассмотрим оценку количества информации, получаемой от аналогового измерительного прибора с длиной рабочей части шкалы, равной L, работающего с погрешностью D, заданной в единицах длины прибора.

Полагаем также, что допустимая погрешность d в заданной измерительной системе меньше той, какую может обеспечить используемый прибор: δ<Δ. Исходя из заданной точности измерений прибор должен гарантировать

точек измерения в пределах рабочей части шкалы, но фактически он может гарантировать только

M₂=L/Δ

точек измерения. Начальная энтропия измерений составляет

а энтропия после измерений –

Количество информации, получаемой от этого прибора, равно

, (2.6)

т.е. определяется его точностью во всех случаях, когда имеет место δ<Δ. При δ=Δ величина H₂ достигает значения H₂=0. Это говорит о том, что измерения производятся с заданной точностью. Заданная точность измерений поддерживается и при δ>Δ, т.е. сохраняется H₂=0. Хотя измерительный прибор при δ>Δ может обеспечить точность измерений больше заданной, это обстоятельство не является определяющим. Ведь величина исчерпывающей информации равна исходной энтропии, на которую сориентирована работа всего измерительного и управляющего комплекса, а точность первичного прибора является лишь одним из многих факторов, определяющих точность измерений. Иными словами, информация будет фиксироваться и преобразовываться в соответствии принятым объемом энтропии, а повышенная точность отдельных звеньев измерительного комплекса не будет учитываться.

Для практических расчетов количества информации по формулам (2.1-2.3) и по формуле (2.5) введем понятие единицы измерения информации. Примем во внимание, что в устройствах хранения, передачи или переработки информации обычно применяются элементы, в которых для записи информации используется только два символа, такие как высокий и низкий потенциалы (в электронных устройствах) или намагниченный и не намагниченный участки магнитных носителей информации. Эти символы обычно обозначают знаками 1 и 0. Использование только двух символов для записи информации соответствует n=2 в формулах (2.1-2.3), и в дальнейших рассуждениях мы так и будем полагать. Тогда окажется, что при исследовании процесса с двумя равновероятными исходами мы получим, в соответствии с формулой (2.1), H₁=1(M₁=2) и H₂=0(M₂=1), что дает, в соответствии с формулой (2.5), информацию I=1.

Информацию, которую получают из опыта с двумя равновероятными исходами, используют в качестве эталона (единицы) количества информации в устройствах, в которых запись информации производится с помощью только двух символов. Эту информацию называют битом, или двоичной единицей информации. Согласно формуле (2.3), количество информации, равное одному биту, можно получить и иным путем, из опыта со многими, но не равновероятными исходами. Опыт с двумя равновероятными исходами, (к которому приближается, например, подбрасывание монеты) является лишь эталоном бита. Из определения бита следует, что максимальное количество информации, которая может храниться в электронном триггере или на элементарном намагниченном участке магнитной дискеты, равно одному биту. По тем же причинам номинальная емкость запоминающих устройств (ЗУ), указанная в битах, есть максимальное количество информации, которое может храниться в этих ЗУ при условии, что все события, сообщения о которых зафиксированы в ЗУ, являются равновероятными. Обычно, в ЗУ зафиксированы сообщения о событиях, которые не равновероятны. Ярким примером такого рода сообщений являются сообщения об отсутствии аварийной ситуации. Их вероятность при нормальном ходе технологического процесса значительно выше вероятности поступления сигнала аварии. По указанным причинам фактический объем информации, хранящейся в ЗУ, значительно меньше номинального. Широко используются производные от бита единицы информации: 1 байт = 8 бит, 1 Кбайт =2¹⁰ байт, 1 Мбайт = 2²⁰ байт и др.

Особой единицей информации является слово. Слово – это количество информации, обрабатываемой в данном управляющем устройстве за один цикл работы устройства. Величина слова обычно кратна по отношению к байту: 1 байт, 2 байт, 4 байт. Если необходимо оценить лишь объем записи информации на электронных или магнитных носителях, то битом называют минимальный объем записи, соответствующий двоичной единице или двоичному нулю (элементарная ячейка памяти).

Кодирование информации

Кодированием мы будем называть процесс формирования сообщений о событиях, составляющих управляемый техпроцесс. Процесс кодирования состоит из двух этапов:

– представление информации в дискретной форме (аналогово-цифровое преобразование);

– представление дискретных сигналов в наиболее подходящем для решения задач управления техпроцессом виде (преобразование кодов).

Конкретный способ представления информации как системы соответствия между элементами сообщений и сигналами, их отображающими, называетсякодом. Информация всегда представлена в каком-либо коде.

Первоначальный код, в котором информация поступает в управляющее устройство, определяется свойствами источника информации. Последний может быть либо датчиком какого-либо технологического параметра, либо некоторым ЗУ. В ЗУ информация уже представлена в дискретной форме, а сигналы датчика преобразуются в дискретную форму первичным преобразователем, свойства которого могут быть не согласованы с требованиями, предъявляемыми к информации, поступающей в управляющее устройство. Необходимое согласование производится соответствующим преобразователем кода, установленным на выходе первичного преобразователя.

По характеру взаимодействия с первичным преобразователем сигналы датчиков делятся на дискретные и непрерывные (аналоговые). Если первичный преобразователь выделяет в сигнале датчика только два (реже три) уровня, то такой сигнал считается дискретным. Характерными дискретными сигналами являются сигналы о включении или выключении технологического оборудования. Если первичный преобразователь выделяет в сигнале датчика много (три и более) уровней, то такой сигнал считается непрерывным. Характерными непрерывными сигналами являются сигналы, регистрируемые стрелочными или самопишущими измерительными приборами. Если сигнал датчика классифицируется в качестве дискретного, то первичный преобразователь должен произвести лишь необходимое усиление сигнала и его гальваническую развязку с управляющим устройством. Если же сигнал датчика воспринимается в качестве непрерывного, то первичный преобразователь, осуществляющий аналого-цифровое преобразование, должен, помимо всего прочего, обеспечить различение необходимого количества уровней сигнала, т.е. должен иметь достаточную разрешающую способность, соответствующую величине энтропии данного элемента технологического объекта. Так, при использовании стрелочных измерительных приборов разрешающая способность обеспечивается выбором подходящей цены деления шкалы, а при использовании импульсных датчиков перемещения разрешающая способность обеспечивается выбором соответствующей величины перемещения контролируемого механизма между двумя соседними импульсами (цены импульса). Разрешающую способность называют также шагом квантования по уровню (см. рис. 2.1а).

При квантовании по уровню непрерывный сигнал x(t) заменяется ступенчатой функцией Ψ(x). Значение последней (рис.2.1а) изменяется только после изменения значения x на величину, не меньшую Dx, которая является шагом квантования и определяет разрешающую способность. При заданной допустимой относительной погрешности d величина шага квантования Dx определяется из соотношения

, (2.7)

где и - максимальное и минимальное значения сигнала в заданном диапазоне его изменения.

Точность измерений зависит не только от разрешающей способности первичного преобразователя, но и от его быстродействия, которое у аналого-цифровых преобразователей (АЦП) определяется частотой отсчета измеряемой величины, т.е. шагом квантования по времени Dt (см. рис. 2.1б). Если принять шаг Dt, равным t_j-t_j_-1 (рис. 2.1а), то в промежутке время между t_j_-1 и t_j измеренное значение x будет равно Dx, а в момент времени t=t_j оно скачком увеличится до величины x=x_j. Видно, что большой шаг квантования по времени привел к значительному увеличению погрешности. При уменьшении шага квантования по времени точность измерения увеличивается. Чтобы точность измерений соответствовала шагу квантования по уровню Dx, величина шага квантования по времени Dt должна быть выбрана исходя из неравенства

. (2.8)

Соотношения (2.7) и (2.8) определяют требования к разрешающей способности и к быстродействию применяемых АЦП.

Отсчет и запоминание измеренной величины х обычно производятся либо в десятичной, либо в двоичной системе исчисления. Тип используемой системы исчисления зависит от примененной системы кодирования. Каждая система кодирования базируется на совокупности четко определенных, специфических сигналов одной физической природы, называемых символами. Полная совокупность символов, на которой базируется система кодирования, составляет ее алфавит. Конечная совокупность символов, входящих в принятую систему кодирования, называется кодовой комбинацией, словом иличислом в зависимости от характера формируемого сообщения. Совокупности слов, правил их формирования и сочетания образуют разнообразные языки кодирования. В системах кодирования АСУТП широко применяется такие совокупности символов, как латинский и русский алфавиты, арабские цифры, знаки препинания, знаки математических операций и другие математические символы.

Для представления чисел обычно используются арифметические коды, в которых любое действительное число может быть представлено в виде

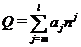, (2.9)

где: n > 1- целое число, основание системы исчисления;

m и l – произвольные числа, причем m l;

a_j- целое число, причем

Произведение называют разрядом закодированного числа, причем называют весом разряда, a_j - цифрой или цифровым значением разряда, a j – номером разряда. Если m=l, то закодированное число одноразрядное, состоит из одного разряда, а если все a_j равны нулю, то Q=0. Все разряды, у которых j < 0 входят в дробную часть закодированного числа, а остальные разряды составляют его целую часть. При записи чисел обычно опускают веса разрядов, а также нули перед первой значащей цифрой целой части числа и после последней значащей цифры дробной части числа, причем дробную часть числа отделяют от целой части запятой или точкой. После этого запись числа принимают более компактный вид:

. (2.10)

В качестве примера рассмотрим запись десятичного числа (n=10), у которого l=-5, m=-4, a_-5=9, a_-4=3. По формуле (2.9) получим:

что в обычной записи составит Q=0,00039.

В управляющих устройствах систем автоматизации наиболее распространена двоичная система исчисления и соответственно для записи числовой информации применяется двоичный арифметический код (n=2). При записи числа в двоичном арифметическом коде используют только две цифры: 0 и 1, так что закодированное число приобретает вид набора нулей и единиц, в котором дробная часть числа отделяется от целой части запятой. В качестве примера рассмотрим запись двоичного числа, у которого m=2, l=-2, по формуле (2.9) получим:

Опустив обозначения весов разрядов, получим, в соответствии с формулой (2.10), запись данного числа в традиционном виде: Q=100,01.

Перевод целой части числа из десятичной в двоичную форму записи удобно производить методом деления. По этому методу исходное десятичное число последовательно делится на 2. Остатки от деления образуют двоичное число, причем старший разряд соответствует последнему остатку, а младший – первому. В качестве примера рассмотрим преобразование десятичного числа 25 в соответствующее двоичное число:

25/2=12 (остаток 1) – младший разряд

12/2=6 (остаток 0)

6/2=3 (остаток 0)

3/2=1 (остаток 1)

1/2=0 (остаток 1) – старший разряд

Полученное двоичное число-

Аналогично в двоичную форму переводится методом умножения дробная часть десятичного числа. В случае необходимости различения двоичных и десятичных (Decimal) чисел в конце двоичного числа ставят букву B (Binary).

Широкое применение при проектировании микропроцессорных управляющих устройств нашел шестнадцатеричный (Hexadecimal) арифметический код (n=16, HEXCODE). Для записи числовой информации в этом коде необходимо иметь 16 цифр. Для обозначения первых 10 из них используются арабские цифры, а остальные 6 цифр имеют следующие обозначения: 10-A, 11-B, 12-C, 13-D, 14-E и 15-F. Запись чисел в 16-ричном коде производится, как и в системах исчисления с другими основаниями, в соответствии с формулами (2.9) и (2.10). В качестве примера рассмотрим 16-ричное число, у которого m=2, l=0, и . По формуле (2.9) получим:

Запись в 16-ричной форме дает, согласно формуле (2.10), Q=4EA.

От 16-ричного кода нетрудно перейти к двоичному коду. Для этого каждую цифру 16-ричного числа заменяют кодовой комбинацией из 4 двоичных символов, записанной в двоичном арифметическом коде и численно равной заменяемой цифре. Из цифр 16-ричного кода предыдущего примера получим: 4=0100, E=14=1110, A=10=1010. Число Q в целом, записанное в двоичном коде, с учетом отбрасывания нуля, стоящего перед первой значащей цифрой, будет выглядеть как:

Q=10011101010.

Для перехода от двоичной формы записи числа к 16-ричной достаточно разбить двоичное число на группы по 4 символа в каждой, начиная с младшего разряда двоичного числа, с последующей заменой каждых четырех двоичных символов на один 16-ричный, и дополняя при необходимости нулями группу старших разрядов. Так, разбивка предыдущего числа, с последующей заменой четырехсимвольных групп 16-ричными цифрами, дает: Q=0100 1110 1010=4EA.

Простота перехода от двоичной к 16-ричной форме записи чисел и обратно обусловила применение 16-ричного кода для компактной записи двоичных кодовых комбинаций, применяемых в микропроцессорных системах управления.

Двоичные коды

Дата добавления: 2018-04-04; просмотров: 612; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!