Обсуждение результатов и формулирование выводов
1). Достигнутая стабильность показателя служебного назначения оценивается полем рассеяния, полученным в ходе эксплуатационных испытаний. Требуемая стабильность задана полем допуска этого показателя. Сравнение этих величин через коэффициент точности позволяет судить, во-первых, о степени достижения требуемой стабильности и возможности сертификации машины по этому показателю или же необходимости анализа возможных причин недостаточной стабильности и их источников. Необходимо адресовать вопросы к участникам процесса создания машины – конструкторам, технологам, а возможно, и к метрологам.
Для оценки степени достижения требуемой стабильности можно руководствоваться следующими рекомендациями:
при КТ > 1,3 достигнутая стабильность показателя считается
удовлетворительной;
при КТ = 1 ÷ 1,3 достигнутая стабильность показателя требует
внимательного наблюдения, так как запас точности недостаточен и
со временем могут появиться изделия за пределами допуска;
при КТ < 1– достигнутая стабильность показателя считается
неудовлетворительной.
2). В случаях появления машин, значения показателя служебного назначения которых выходят за пределы допуска, следует высказать предложения о возможных действиях разных участников процесса создания машины для устранения причин появления таких машин.
В примере в изготовленной партии отливок бракованных не оказалось, но опасность их появления при эксплуатации сохраняется, о чем свидетельствует низкий коэффициент точности КТ = 0,83 и вызванный этой причиной теоретически возможный (вероятный) процент брака Б ≈ 1,5%. Превышающее заданный допуск поле рассеяния скорее всего вызвано особенностями технологического процесса литья. Следует проанализировать технологию и если стабильность процесса повысить невозможно, сертифицировать литейную форму для получения отливок 7 класса размерной точности.
|
|
|
Приложение 1
Задание №__. Спроектирована и изготовлена металлическая литейная форма для получения отливок по 6 классу размерной точности из стали и цветных сплавов. В ходе эксплуатационных испытаний изготовлено 100 отливок и в них измерен полученный размер, номинальное значение которого 200 мм. Поле допуска на этот размер отливки по 6 классу размерной точности равно 0,8 мм при симметричном расположении относительно номинала. Результаты измерений этого размера в отливках опытной партии приведены в таблице. Оценить достигнутую стабильность размера в партии отливок.
| 210,03 | 209,89 | 209,91 | 210,23 | 210,01 | 209,71 | 210,12 | 209,83 |
| 210,36 | 210,11 | 210,03 | 210,3 | 210,3 | 210,15 | 210,14 | 210,3 |
| 209,96 | 210,25 | 209,86 | 210,26 | 209,96 | 210,2 | 209,98 | 210,04 |
| 210,12 | 209,92 | 210,15 | 210,11 | 210,03 | 210,27 | 209,86 | 210,01 |
| 209,91 | 210,3 | 209,91 | 210 | 209,86 | 210,29 | 209,99 | 209,81 |
| 210,05 | 210,06 | 209,93 | 210,24 | 209,7 | 209,76 | 210,06 | 210,03 |
| 210,16 | 210,37 | 210,13 | 209,83 | 209,99 | 209,9 | 210 | 210,2 |
| 209,9 | 210,22 | 210,22 | 209,75 | 210,06 | 209,86 | 210,2 | 210 |
| 210,15 | 210,26 | 209,97 | 210,24 | 210,1 | 210 | 209,92 | 209,61 |
| 210,09 | 209,99 | 209,81 | 210,28 | 209,88 | 210,1 | 210,08 | |
| 210,25 | 210,14 | 210,31 | 210,4 | 209,73 | 209,99 | 210,1 | |
| 210,22 | 210,41 | 209,77 | 209,95 | 209,76 | 209,88 | 210 | |
| 209,88 | 210,05 | 210,14 | 209,96 | 209,91 | 210,3 | 209,76 |
|
|
|
Приложение 2
Значения ординат кривой Гаусса при 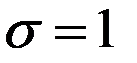 ;
; 
| Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.0 | 0.3989 | 0.3989 | 0.3989 | 0.3988 | 0.3986 | 0.3984 | 0.3982 | 0.3980 | 0.3977 | 0.3973 |
| 0.1 | 0.3970 | 0.3965 | 0.3961 | 0.3956 | 0.3951 | 0.3945 | 0.3939 | 0.3932 | 0.3925 | 0.3918 |
| 0.2 | 0.3910 | 0.3902 | 0.3894 | 0.3885 | 0.3876 | 0.3867 | 0.3857 | 0.3847 | 0.3836 | 0.3825 |
| 0.3 | 0.3814 | 0.3802 | 0.3790 | 0.3778 | 0.3765 | 0.3752 | 0.3739 | 0.3725 | 0.3712 | 0.3697 |
| 0.4 | 0.3683 | 0.3668 | 0.3653 | 0.3637 | 0.3625 | 0.3605 | 0.3589 | 0.3572 | 0.3555 | 0.3538 |
| 0.5 | 0.3521 | 0.3503 | 0.3485 | 0.3467 | 0.3448 | 0.3429 | 0.3410 | 0.3391 | 0.3372 | 0.3352 |
| 0.6 | 0.3332 | 0.3312 | 0.3292 | 0.3271 | 0.3251 | 0.3230 | 0.3209 | 0.3187 | 0.3166 | 0.3144 |
| 0.7 | 0.3123 | 0.3101 | 0.3079 | 0.3056 | 0.3034 | 0.3011 | 0.2989 | 0.2966 | 0.2943 | 0.2920 |
| 0.8 | 0.2897 | 0.2874 | 0.2850 | 0.2827 | 0.2803 | 0.2780 | 0.2756 | 0.2732 | 0.2709 | 0.2685 |
| 0.9 | 0.2661 | 0.2637 | 0.2613 | 0.2589 | 0.2565 | 0.2541 | 0.2516 | 0.2492 | 0.2468 | 0.2444 |
| 1.0 | 0.2420 | 0.2396 | 0.2371 | 0.2347 | 0.2323 | 0.2299 | 0.2275 | 0.2251 | 0.2227 | 0.2203 |
| 1.1 | 0.2179 | 0.2155 | 0.2131 | 0.2107 | 0.2083 | 0.2059 | 0.2036 | 0.2012 | 0.1989 | 0.1965 |
| 1.2 | 0.1942 | 0.1919 | 0.1895 | 0.1872 | 0.1849 | 0.1826 | 0.1804 | 0.1781 | 0.1758 | 0.1736 |
| 1.3 | 0.1714 | 0.1691 | 0.1669 | 0.1647 | 0.1626 | 0.1604 | 0.1582 | 0.1561 | 0.1539 | 0.1518 |
| 1.4 | 0.1497 | 0.1476 | 0.1456 | 0.1435 | 0.1415 | 0.1394 | 0.1374 | 0.1354 | 0.1334 | 0.1315 |
| 1.5 | 0.1295 | 0.1276 | 0.1257 | 0.1238 | 0.1219 | 0.1200 | 0.1182 | 0.1163 | 0.1145 | 0.1127 |
| 1.6 | 0.1109 | 0.1092 | 0.1074 | 0.1057 | 0.1040 | 0.1023 | 0.1006 | 0.0983 | 0.0973 | 0.0957 |
| 1.7 | 0.0940 | 0.0925 | 0.0909 | 0.0893 | 0.0878 | 0.0863 | 0.0848 | 0.0833 | 0.0818 | 0.0804 |
| 1.8 | 0.0790 | 0.0775 | 0.0761 | 0.0748 | 0.0734 | 0.0721 | 0.0707 | 0.0694 | 0.0681 | 0.0669 |
|
|
|
Приложение 3
Определение процента вероятного брака
| Тn | Абсолютные значения коэффициента смещения Е или Ер | ||||||||||||||
| 0 | 0.02 | 0.05 | 0.08 | 0.10 | 0.12 | 0.15 | 0.18 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | |
| 0.10 | 76.4 | 76.4 | 76.4 | 76.4 | 76.5 | 76.5 | 76.5 | 76.5 | 76.6 | 76.7 | 76.8 | 76.9 | 77.1 | 77.2 | 77.4 |
| 0.15 | 65.3 | 65.3 | 65.3 | 65.4 | 65.4 | 65.5 | 65.6 | 65.7 | 65.8 | 66.1 | 66.4 | 66.8 | 67.3 | 67.8 | 68.4 |
| 0.20 | 54.8 | 54.9 | 54.9 | 55.0 | 55.0 | 55.3 | 55.5 | 55.8 | 56.0 | 56.6 | 57.4 | 58.2 | 59.2 | 60.3 | 61.5 |
| 0.25 | 45.3 | 45.3 | 45.4 | 45.6 | 45.8 | 46.0 | 46.5 | 47.0 | 47.3 | 48.4 | 49.7 | 51.2 | 52.9 | 54.7 | 56.7 |
| 0.30 | 36.8 | 36.8 | 37.0 | 37.3 | 37.6 | 37.9 | 38.5 | 39.2 | 39.8 | 41.5 | 43.4 | 45.7 | 48.1 | 50.8 | 53.6 |
| 0.35 | 29.4 | 29.4 | 29.6 | 30.1 | 30.4 | 30.9 | 31.7 | 32.8 | 33.5 | 35.8 | 38.4 | 41.4 | 44.6 | 48.1 | 51.8 |
| 0.40 | 23.0 | 23.1 | 23.4 | 23.9 | 24.3 | 24.9 | 26.0 | 27.3 | 28.2 | 31.0 | 34.3 | 38.0 | 42.1 | 46.4 | 50.8 |
| 0.42 | 20.8 | 20.8 | 21.1 | 21.7 | 22.2 | 22.8 | 24.0 | 25.3 | 26.4 | 29.4 | 32.9 | 36.9 | 41.2 | 45.8 | 50.6 |
| 0.45 | 17.7 | 17.7 | 18.1 | 18.7 | 19.3 | 19.9 | 21.2 | 22.7 | 23.8 | 27.1 | 31.0 | 35.4 | 40.1 | 45.1 | 50.4 |
| 0.48 | 15.0 | 15.1 | 15.4 | 16.1 | 16.7 | 17.4 | 18.7 | 20.4 | 21.6 | 25.1 | 29.3 | 34.0 | 39.2 | 44.6 | 50.2 |
| 0.50 | 13.4 | 13.4 | 13.8 | 14.5 | 15.1 | 15.8 | 17.2 | 18.9 | 20.2 | 23.9 | 28.2 | 33.2 | 38.6 | 44.3 | 50.1 |
| 0.55 | 9.89 | 10.0 | 10.4 | 11.1 | 11.7 | 12.6 | 14.0 | 15.8 | 17.2 | 21.1 | 25.9 | 31.3 | 37.2 | 43.5 | 50.1 |
| 0.60 | 7.19 | 7.26 | 7.65 | 8.37 | 9.03 | 9.84 | 11.3 | 13.2 | 14.6 | 18.8 | 23.9 | 29.6 | 36.0 | 42.9 | 50.1 |
| 0.65 | 5.12 | 5.19 | 5.56 | 6.25 | 6.90 | 7.69 | 9.17 | 11.0 | 12.4 | 16.7 | 21.9 | 28.0 | 34.9 | 42.3 | 50.0 |
| 0.70 | 3.57 | 3.64 | 3.98 | 4.63 | 5.24 | 5.98 | 7.40 | 9.16 | 10.5 | 14.8 | 20.1 | 26.4 | 33.7 | 41.7 | 50.0 |
| 0.75 | 2.44 | 2.50 | 2.89 | 3.40 | 3.94 | 4.62 | 5.94 | 7.61 | 8.94 | 13.1 | 18.4 | 25.0 | 32.6 | 41.1 | 50.0 |
| 0.80 | 1.64 | 1.69 | 1.95 | 2.46 | 2.94 | 3.55 | 4.75 | 6.29 | 7.53 | 11.5 | 16.8 | 23.6 | 31.5 | 40.5 | 50.0 |
| 0.85 | 1.08 | 1.12 | 1.34 | 1.76 | 2.19 | 2.71 | 3.76 | 5.17 | 6.32 | 10.1 | 15.4 | 22.2 | 30.5 | 39.9 | 50.0 |
| 0.90 | 0.69 | 0.72 | 0.90 | 1.26 | 1.60 | 2.05 | 2.96 | 4.21 | 5.27 | 8.85 | 14.1 | 20.9 | 29.5 | 39.4 | 50.0 |
| 0.95 | 0.44 | 0.46 | 0.60 | 0.80 | 1.16 | 1.51 | 2.31 | 3.42 | 4.36 | 7.71 | 12.7 | 19.6 | 28.4 | 38.8 | 50.0 |
|
|
|
Практическая работа № 2
Расчет допусков линейных размеров по единице допуска
Цель работы. Ознакомиться с основными понятиями и принципами построения системы допусков.
Теоретические предпосылки.
Вал - это термин, условно применяемый для обозначения наружных элементов деталей, включая и нецилиндрические элементы (См. рис 1.1). Вал обозначается прописной буквой латинского алфавита – d. Отверстие – это термин, условно применяемый для обозначения внутренних элементов деталей, включая и нецилиндрические элементы. Отверстие обозначается заглавной буквой латинского алфавита – D. Размер - это числовое значение линейной величины (диаметра, длины и т.п.) в выбранных единицах измерения.

| 
|
| Рис. 1.1 | Рис. 1.2 |
База - это элемент детали (или выполняющее ту же функцию сочетание элементов), по отношению к которому задается допуск расположения рассматриваемого элемента, а также определяется соответствующее отклонение. Отклонение - это алгебраическая разность между размером (действительным или предельным размером) и соответствующим номинальным размером (См. рис. 1.2). Предельное отклонение - это алгебраическая разность между предельным и соответствующим номинальным размерами. Различают верхнее и нижнее предельные отклонения. Верхнее отклонение - это алгебраическая разность между наибольшим предельным и соответствующим номинальным размерами ES - верхнее отклонение отверстия, es - верхнее отклонение вала. Нижнее отклонение - это алгебраическая разность между наименьшим предельным и соответствующим номинальным размерами. EI - нижнее отклонение отверстия, ei - нижнее отклонение вала. Поле допуска – поле, ограниченное наибольшим и наименьшим предельными размерами и определяемое величиной допуска и его положением относительно нулевой линии, соответствующей номинальному размеру.
Допуск (IT) - это разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями. Допуск является скалярной величиной без знака. Единица допуска (i, I) - это множитель в формулах допусков, являющийся функцией номинального размера и служащий для определения числового значения допуска. Квалитет - это совокупность допусков, рассматриваемых как соответствующие одному уровню точности для всех номинальных размеров.
Системой допусков и посадок (СДП) называется совокупность рядов допусков и посадок, закономерно построенных на основе опыта, теоретических и экспериментальных исследований и оформленных в виде стандартов. Система предназначена для выбора минимально необходимых, но достаточных для практики вариантов допусков и посадок типовых соединений деталей машин, что создает предпосылки для стандартизации режущих инструментов и калибров, облегчает конструирование, производство и ремонт изделий и т.д..
Стандартом установлены квалитеты: 01, 0, 1, 2, 3, 4, 5, …, 11, 12…18. Самые точные квалитеты 01, 0, 1, 2, 3, 4, как правило, применяются при изготовлении образцовых мер и калибров. Квалитеты с 5-го по 11-й, как правило, применяются для сопрягаемых элементов деталей. Квалитеты с 12-го по 18-й применяются для несопрягаемых элементов деталей. Чтобы максимально сократить число значений допусков при построении рядов допусков, стандартом установлены интервалы размеров, внутри которых значение допуска для данного квалитета не меняется (см. табл. 1.2).
Допуск IT рассчитывается по формуле:
IT = k * i
где k – число единиц допуска, установленное для каждого квалитета; i – единица допуска, зависящая только от размера (табл. 1.1).
Таблица 1.1. (Таблица дана в сокращении)[1]
| Квалитет | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Число единиц допуска k | 7 | 10 | 16 | 25 | 40 | 64 | 100 | 160 | 250 | 400 | 640 | 1000 | 1600 | 2500 |
| Допуск для размеров до 500 мм | IT = k * i где i = 0,45 * D1/3 + 0,001 * D, мкм | |||||||||||||
| Допуск для размеров свыше 500 до 3150 мм | IT = k * I где I = 0,004 * D + 2,1, мкм | |||||||||||||
| Примечания: D – среднее геометрическое из крайних значений каждого интервала номинальных размеров, мм | ||||||||||||||
Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Более формально:
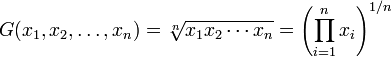
Последовательность выполнения работы.
1. Изучить теоретические предпосылки, приведенные в данном методическом указании.
2. Получить задание у преподавателя.
3. Рассчитать величины допусков для предложенных допусков и квалитетов.
4. Сравните полученные величины с табличными (табл. 1.2).
5. Сделать выводы о проделанной работе.
Контрольные вопросы.
1. Что такое система допусков и посадок? С какой целью была разработана система допусков и посадок?
2. Что такое допуск? Что такое единица допуска? Сколько единиц допуска содержит допуск на размер по 11 квалитету?
3. Что такое квалитет?
4. По какой формуле (по единице допуска) рассчитывается допуск для размеров до 500 мм?
Табл. 1.2. Значения допусков, мкм (дана в сокращении)
| Интервал номинальных размеров, мм | Квалитет | ||||||||||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| До 3 | 4 | 6 | 10 | 14 | 25 | 40 | 60 | 100 | 140 | 250 | 400 |
| Св. 3 до 6 | 5 | 8 | 12 | 18 | 30 | 48 | 75 | 120 | 180 | 300 | 480 |
| Св. 6 до 10 | 6 | 9 | 15 | 22 | 36 | 58 | 90 | 150 | 220 | 360 | 580 |
| Св. 10 до 18 | 8 | 11 | 18 | 27 | 43 | 70 | 110 | 180 | 270 | 430 | 700 |
| Св. 18 до 30 | 9 | 13 | 21 | 33 | 52 | 84 | 130 | 210 | 330 | 520 | 840 |
| Св. 30 до 50 | 11 | 16 | 25 | 39 | 62 | 100 | 160 | 250 | 390 | 620 | 1000 |
| Св. 50 до 80 | 13 | 19 | 30 | 46 | 74 | 120 | 190 | 300 | 460 | 740 | 1200 |
| Св. 80 до 120 | 15 | 22 | 35 | 54 | 87 | 140 | 220 | 350 | 540 | 870 | 1400 |
| Св. 120 до 180 | 18 | 25 | 40 | 63 | 100 | 160 | 250 | 400 | 630 | 1000 | 1600 |
| Св. 180 до 250 | 20 | 29 | 46 | 72 | 115 | 185 | 290 | 460 | 720 | 1150 | 1850 |
Практическая работа № 3.
Дата добавления: 2018-04-04; просмотров: 257; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
