Моделирование уровня оптимальных запасов

Теоретическое введение

Рассмотрим простейшие математические модели управления запасами. На рисунке 3.1. представлены возможные графики изменения запаса Q, имеющегося на складе, во времени t, для которого рассматривается этот запас.

Рисунок 3.1 –Графики изменения запасов

Под Q будем понимать изделия или материалы (товары) только одного вида. Если на изделие поступает заявка, то оно отпускается и значение Q падает. Предположим, что величина спроса непрерывна во времени. Если Q = 0, то имеет место дефицит.

Любая математическая модель, которая применяется для изучения определенной ситуации в управлении запасами, должна учитывать факторы, связанные с издержками.

Различают организационные издержки — расходы, связанные с оформлением и доставкой товаров, издержки содержания запасов -- затраты, связанные с хранением. Они возникают из-за амортизации в процессе хранения (изделия могут портиться, устаревать, их количество может уменьшаться и т.д.). Существуют издержки, связанные с дефицитом: если поставка со склада не может быть выполнена, то возникают дополнительные издержки, связанные с отказом. Это может быть денежный штраф или ущерб, не осязаемый непосредственно (например, ухудшение бизнеса в будущем и потеря потребителей). Количество товара, поставляемое на склад, называют размером партии.

Модели управления запасами.

Любая модель управления запасами должна дать ответ на два вопроса:

1. Какое количество продукции заказывать?

2. Когда заказывать?

Ответ на первый вопрос выражается через размер заказа, определяющего оптимальное количество ресурсов, которое необходимо поставлять каждый раз, когда происходит размещение заказа. В зависимости от рассматриваемой ситуации размер заказа может меняться во времени. Ответ на второй вопрос зависит от типа системы управления запасами. Если система предусматривает периодический контроль состояния запаса через равные промежутки времени (например, еженедельно или ежемесячно), момент поступления нового заказа обычно совпадает с началом каждого интервала времени. Если же в системе предусмотрен непрерывный контроль состояние запаса, точка заказа обычно определяется уровнем запаса, при котором необходимо размещать новый заказ.

Таким образом, решение обобщённой задачи управления запасами определяется следующим образом;

1. В случае периодического контроля состояния запаса следует обеспечивать поставку нового количества ресурсов в объеме размера заказа через равные интервалы времени.

2. В случае непрерывного контроля состояния запаса необходимо размещать новый заказ в размере объема запаса, когда его уровень достигает точки заказа.

Размер и точка заказа обычно определяются из условий минимизации суммарных затрат системы управления запасами.

Затраты на приобретение становятся важным фактором, когда цена единицы продукции зависит от размера заказа, что обычно выражается в виде оптовых скидок в тех случаях, когда цена единицы продукции убывает с возрастанием размера заказа. Затраты на оформление заказа представляют собой постоянные расходы, связанные с его размещением. Таким образом, при удовлетворении спроса в течение заданного периода времени путем размещения более мелких заказов (более часто) затраты возрастают по сравнению со случаем, когда спрос удовлетворяется посредством более крупных заказов (и, следовательно реже). Затраты на хранение запаса, которые представляют собой расходы на содержание запаса на складе (например, процент на инвестированный капитал, затраты на переработку, амортизационные расходы и эксплутационные расходы), обычно возрастают с увеличением уровня запаса. Наконец, потеря дефицита представляют собой расходы, обусловленные отсутствием запаса необходимой продукции. Обычно они связаны с ухудшением репутации поставщика у потребителя и с потенциальными потерями прибыли.

Оптимальный уровень запаса соответствует минимуму суммарных затрат. Отметим, что модель управления запасами не обязательно должна включать все четыре вида затрат, так как некоторые из них могут быть не значительными, а иногда учёт всех видов затрат чрезмерно усложняет функцию суммарных затрат. На практике какую – либо компоненту затрат можно не учитывать при условии, что она не составляет существенную часть общих затрат.

Обобщенная модель управления запасами, описанная выше выглядит довольно простой. Чем же тогда объясняется столь большое разнообразие моделей этого класса и методов решения соответствующих задач, базирующихся на различном математическом аппарате: от простых схем дифференциального и интегрального исчисления до сложных алгоритмов динамического и других видов математического программирования? Ответ на этот вопрос определяется характером спроса, который может быть детерминированным (достоверно известным) или вероятностным (задаваемым плотностью вероятности). Детерминированный спрос может быть статическим, в том смысле, что интенсивность потребления остаётся неизменной во времени, или динамическим, когда спрос известен достоверно, но изменяется в зависимости от времени. Вероятностный спрос может быть стационарным, когда функция плотности вероятности спроса неизменна во времени, и не стационарным, когда функция плотности вероятности спроса изменяется во времени.

В реальных условиях случай детерминированного статистического спроса встречается редко. Такой случай можно рассматривать как простейший.

Наиболее точно характер спроса может быть описан посредством вероятностных нестационарных распределений. Однако с математической точки зрения модель значительно усложняется, особенно при увеличении рассматриваемого периода времени. Возрастание математической сложности модели управления запасами при переходе от детерминированного статического спроса к вероятностному стационарному спросу, по существу, классификацию можно считать представлением различных уровней абстракции описания спроса.

Важным фактором с точки зрения формулировки и решения задачи является также вид функции затрат. Используются различные методы решения, включающие классическую схему оптимизации, линейное и динамическое программирование. Эти примеры наглядно показывают, что при решении задач управления запасами следует применять различные методы оптимизации.

Введем обозначения необходимых для составления модели. Данные поместим в таблицу 3.1.

Таблица 3.1.

Величина	Обозна- чение	Единица измерения	Предложения
Интенсивность спроса	g	Единиц товара в год	Спрос постоянен и непрерывен. Весь спрос удовлетворяется
Организационные издержки	b	Рублей за год	Издержки постоянны и не зависят от размера партии
Стоимость товара	s	Рублей за год	Цена единицы товара постоянна. Рассматривается один вид товара.
Издержки содержания запасов	h	Рублей за единицу товара в год	Стоимость хранения единицы товара в течение года постоянна.
Размер партии	q	Единица товара в одной партии	Размер партии постоянен. Поступление товара происходит мгновенно, как только уровень запасов равен нулю.

График изменения запасов представлен на рисунке 3.2.

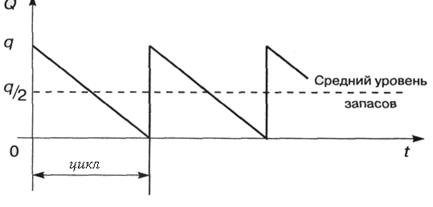
Рисунок 3.2- График изменения запасов

Чтобы полностью удовлетворить годовой спрос g при размере поставки q, необходимо обеспечить g/q поставок или партий за год. Средний уровень запасов составляет q/2.

Уравнение издержек будет иметь вид

(3.1)

Где С₁- общие организационные издержки;

С₂- стоимость товаров;

С₃-общие издержки содержания запасов.

За исключением q все величины в правой части уравнения постоянны и известны, т.е. C=f(q). Для нахождения минимума С найдем производную и приравняем ее к нулю:

(3.2)

откуда , (3.3)

где q_опт- оптимальный размер партии.

Иногда возникает соблазн заказывать размер партии товаров, не соответствующий оптимальному размеру. Это приводит к увеличению издержек на содержание и организацию поставок. Покажем, что это так.

Предположим, что вместо оптимального размера была заказана партия товаров, равная 0.5q_опт. Из основного уравнения издержек выразим составляющие С₁ и С₃. Получим

Таким образом, заказ партии товаров размером 0.5q_опт (вместо q_опт) приводит к увеличению общих издержек на содержание запасов и организацию поставок на 25%. Аналогичная картина наблюдается в случае заказа поставок больше чем q_опт_.

Изобразим графически изменение отдельных составляющих величин С.

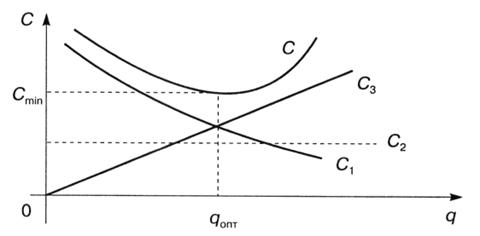
Рисунок 3.3- Изменение составляющих функции затрат

Из рисунка 3.3 следует, что увеличение q ведет к резкому снижению С₁ , при этом С₃ увеличивается пропорционально h/2 .

Дата добавления: 2018-04-04; просмотров: 723; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 7 8910 11 12 Следующая ⇒

Мы поможем в написании ваших работ!