Системы массового обсЛуживания
Задание 1.
В систему массового обслуживания (СМО) поступает в среднем λ заявок [1/час]. Найти вероятность того, что за время t [мин] в СМО поступит:
а) ровно k заявок;
б) менее k заявок;
в) более k заявок.
Варианты задания:
1. λ = 60; t = 5; k = 4.
2. λ = 120; t = 2; k = 3.
3. λ = 40; t = 6; k = 5.
4. λ = 30; t = 4; k = 4.
5. λ = 150; t = 3; k = 3.
6. λ = 80; t = 2; k = 5.
7. λ = 40; t = 3; k = 4.
8. λ = 100; t = 2; k = 3.
9. λ = 60; t = 5; k = 4.
10. λ = 40; t = 4; k = 5.
Задание 2.
Испытывают три элемента, работающих независимо друг от друга. Длительность времени безотказной работы элементов распределена по показательному закону и равна t1, t2, t3 [час]. Найти вероятность того, что в интервале времени [0, tотк] откажут:
а) только один элемент;
б) не более 2-х элементов;
в) все три элемента.
Варианты задания:
1. t1 = 20; t2 = 50; t3 = 40; tотк = 18.
2. t1 = 10; t2 = 20; t3 = 25; tотк = 15.
3. t1 = 20; t2 = 8; t3 = 10; tотк = 6.
4. t1 = 8; t2 = 4; t3 = 5; tотк = 3.
5. t1 = 10; t2 = 5; t3 = 4; tотк = 5.
6. t1 = 12; t2 = 9; t3 = 12; tотк = 8.
7. t1 = 16; t2 = 12; t3 = 26; tотк = 12.
8. t1 = 14; t2 = 10; t3 = 18; tотк = 18.
9. t1 = 10; t2 = 25; t3 = 14; tотк = 16.
10. t1 = 22; t2 = 16; t3 = 18; tотк = 15.
Задание 3.
Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:
|
|
|
а) построить размеченный граф состояний;
б) найти распределение вероятностей для первых 3-х шагов, если известно, что в начальный момент времени (t0 = 0) система находилась в j-ом состоянии с вероятностью pj(0).
Варианты задания:
| 1 |

|
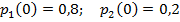
|
| 2 |

|

|
| 3 |

|

|
| 4 |

|

|
| 5 |

|

|
| 6 |

|

|
| 7 |

|

|
| 8 |

|

|
| 9 |

|

|
| 10 |

|

|
Задание 4.
Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие. Требуется:
а) составить матрицу интенсивностей переходов;
б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;
в) найти предельное распределение вероятностей.
Варианты задания:
| 1 | 
| 6 | 
|
| 2 | 
| 7 | 
|
| 3 | 
| 8 | 
|
| 4 | 
| 9 | 
|
| 5 | 
| 10 | 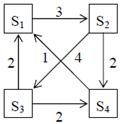
|
Задание 5.
Рассматривается n-канальная система массового обслуживания (СМО) с отказами. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час]. Среднее время обслуживания заявки равно tоб [мин]. Время обслуживания распределено по показательному закону. Определить:
|
|
|
а) число каналов, при котором вероятность того, что заявка получит отказ, не больше α;
б) абсолютную пропускную способность СМО;
в) среднее число каналов, занятых обслуживанием заявок;
г) среднее время пребывания заявки в СМО;
д) среднее время простоя одного (произвольно взятого) канала.
Варианты задания:
1. λ = 12; tоб = 12; α = 0,07. 6.λ = 6; tоб = 15; α = 0,02.
2. λ = 13; tоб = 12; α = 0,08. 7.λ = 7; tоб = 15; α = 0,03.
3. λ = 19; tоб = 6; α = 0,04. 8.λ = 11; tоб = 12; α = 0,05.
4. λ = 9; tоб = 15; α = 0,06. 9.λ = 5; tоб = 30; α = 0,07.
5. λ = 9; tоб = 12; α = 0,03. 10.λ = 11; tоб = 15; α = 0,09.
Задание 6.
Рассматривается n-канальная система массового обслуживания (СМО) с ожиданием. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час]. Среднее время обслуживания заявки равно tоб [мин]. Время обслуживания распределено по показательному закону. Определить:
а) существует ли стационарный режим работы СМО;
б) среднее число заявок, находящихся в СМО;
в) среднее время пребывания заявки в СМО;
г) вероятность того, что все каналы заняты;
|
|
|
д) среднее время простоя одного (произвольно взятого) канала.
| Варианты | n | λ | tоб |
| 1 | 5 | 18 | 15 |
| 2 | 4 | 5 | 30 |
| 3 | 3 | 18 | 6 |
| 4 | 5 | 30 | 6 |
| 5 | 4 | 19 | 6 |
| 6 | 3 | 10 | 12 |
| 7 | 5 | 22 | 12 |
| 8 | 4 | 20 | 7,5 |
| 9 | 3 | 14 | 7,5 |
| 10 | 3 | 12 | 12 |
Задание 7.
Рассматривается n-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно m. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час]. Среднее время обслуживания заявки равно tоб [мин]. Время обслуживания распределено по показательному закону.
Варианты задания:
1.n = 4; m = 3; λ = 6; tоб = 40. Определить:
а) среднее число заявок, находящихся под обслуживанием;
б) вероятность того, что заявка сразу же будет принята к обслуживанию;
в) вероятность того, что в СМО будет не более 2-х заявок.
2.n = 3; m = 4; λ = 8; tоб = 15. Определить:
а) вероятность того, что заявка получит отказ в обслуживании;
б) среднее число каналов, не занятых обслуживанием;
в) среднее время пребывания заявки в СМО;
3.n = 4; m = 2; λ = 4; tоб = 60. Определить:
а) среднее число заявок в СМО;
б) среднее время пребывания заявки в очереди;
в) вероятность того, что будет простаивать не более одного канала.
|
|
|
4. n = 3; m = 3; λ = 6; tоб = 20. Определить:
а) относительную пропускную способность СМО;
б) среднее число каналов, занятых обслуживанием заявок;
в) среднее время пребывания заявки в СМО.
5.n = 3; m = 4; λ = 9; tоб = 20. Определить:
а) абсолютную пропускную способность СМО;
б) среднее число заявок в очереди;
в) вероятность того, что не более 2-х каналов будут заняты обслуживанием заявок.
6.n = 3; m= 3; λ = 5; tоб = 30. Определить:
а) вероятность того, что заявка получит отказ в обслуживании;
б) среднее число заявок, находящихся под обслуживанием;
в) вероятность того, что менее 2-х заявок будут находиться в очереди на обслуживание.
7.n = 2; m = 4; λ = 6; tоб = 15. Определить:
а) среднее число свободных каналов;
б) вероятность того, что заявка будет принята в СМО;
в) вероятность того, что заявка, поступившая в СМО, встанет в очередь на
обслуживание.
8. n = 4; m = 3; λ = 5; tоб = 30. Определить:
а) среднее число заявок, находящихся в СМО;
б) вероятность того, что заявка сразу же будет принята к обслуживанию;
в) вероятность того, что не более 2-х каналов будет занято обслуживанием заявок.
9.n = 4; m= 3; λ = 9; tоб = 20 . Определить:
а) абсолютную пропускную способность;
б) среднее время пребывания заявки в СМО;
в) среднее число заявок в очереди.
10.n = 3; m= 4; λ = 6; tоб = 15 . Определить:
а) относительную пропускную способность СМО;
б) среднее время ожидания заявки в очереди;
в) среднее число занятых каналов.
Задание 8.
Рассматривается n-канальная система массового обслуживания (СМО) без ограничения на длину очереди, но с ограничением на время ожидания. Заявка ожидает обслуживания в среднем tож [мин], а затем покидает СМО. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час], среднее время обслуживания заявки равно tоб [мин].
Варианты задания:
1.n = 4; λ = 8; tоб = 15; tож = 5. Определить:
а) абсолютную пропускную способность СМО;
б) среднее число заявок в очереди;
в) вероятность того, что в очереди будут находиться не более 2-х заявок.
2.n = 3; λ = 6; tоб = 30; tож = 15. Определить:
а) среднее число заявок, находящихся под обслуживанием;
б) вероятность того, что заявка уйдет из очереди не обслуженной;
в) вероятность того, что менее 3-х заявок будут находиться в очереди на обслуживание.
3.n = 4; λ = 9; tоб = 20; tож = 10. Определить:
а) вероятность того, что заявка будет обслужена;
б) среднее время пребывания заявки в СМО;
в) среднее число свободных каналов.
4.n = 3; λ = 10; tоб = 15; tож = 12. Определить:
а) среднее число заявок, находящихся в СМО;
б) вероятность того, что заявка сразу же будет принята к обслуживанию;
в) среднее время простоя канала.
5.n = 3; λ = 8; tоб = 30; tож = 10. Определить:
а) среднее число заявок в очереди;
б) абсолютную пропускную способность СМО;
в) среднее время пребывания заявки в СМО.
6.n = 4; λ = 10; tоб = 15; tож = 6. Определить:
а) среднее число занятых каналов;
б) относительную пропускную способность СМО;
в) среднее время ожидания заявки в очереди.
7.n = 3; λ = 6; tоб = 20; tож = 12. Определить:
а) вероятность того, что заявка сразу же будет принята к обслуживанию;
б) среднее число заявок, находящихся под обслуживанием;
в) вероятность того, что в СМО будет не более 4-х заявок.
8.n = 4; λ = 12; tоб = 12; tож = 6. Определить:
а) вероятность того, что заявка уйдет из СМО не обслуженной;
б) среднее время пребывания заявки в СМО;
в) среднее число каналов, не занятых обслуживанием.
9.n = 3; λ = 15; tоб = 12; tож = 3. Определить:
а) среднее число заявок в СМО;
б) среднее время простоя канала;
в) вероятность того, что будет простаивать не более одного канала.
10.n = 4; λ = 10; tоб = 12; tож = 3. Определить:
а) относительную пропускную способность СМО;
б) среднее время пребывания заявки в СМО;
в) среднее число каналов, занятых обслуживанием заявок.
Задание 9.
Рассматривается n-канальная система массового обслуживания (СМО) замкнутого типа с m источниками заявок. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час], среднее время обслуживания заявки равно tоб [мин].
Варианты задания:
1.n = 2; m = 7; λ = 3; tоб = 15. Определить:
а) среднее число заявок, находящихся под обслуживанием;
б) среднее время ожидания заявки в очереди;
в) вероятность того, что не менее 4-х источников будут находиться в активном
состоянии.
2.n = 3; m= 8; λ= 2; tоб = 20. Определить:
а) среднее число заявок в очереди;
б) среднее время простоя источника;
в) вероятность того, что не более 5-ти источников будут находиться в пассивном
состоянии.
3.n = 2; m = 8; λ = 1; tоб = 30. Определить:
а) среднее число заявок в СМО;
б) вероятность того, что поступившая заявка сразу же будет принята к обслуживанию;
в) вероятность того, что не менее 4-х заявок будут ожидать в очереди на обслуживание.
4.n = 3; m = 7; λ= 2; tоб = 15. Определить:
а) среднее число простаивающих каналов;
б) вероятность того, что поступившая заявка встанет в очередь для ожидания начала
обслуживания;
в) вероятность того, что будет простаивать не более одного канала.
5.n = 4; m = 8; λ = 3; tоб = 12. Определить:
а) среднее число занятых каналов;
б) среднее время простоя канала;
в) вероятность того, что более 2-х источников будут находиться в активном состоянии.
6.n = 3; m = 7; λ= 4; tоб = 10. Определить:
а) вероятность того, что произвольный источник находится в активном состоянии
(коэффициент готовности);
б) среднее время пребывания заявки в СМО;
в) вероятность того, что в очереди на обслуживание будет более 2-х заявок.
7.n = 3; m = 8; λ = 3; tоб = 10. Определить:
а) среднее число заявок в очереди;
б) вероятность того, что поступившая заявка немедленно будет принята к
обслуживанию;
в) вероятность того, что заняты все каналы.
8.n = 2; m = 8; λ = 2; tоб = 12. Определить:
а) среднее число источников, находящихся в пассивном состоянии;
б) вероятность того, что поступившая заявка встанет в очередь для ожидания начала
обслуживания;
в) вероятность того, что в очереди на обслуживание окажется не более 3-х заявок.
9.n = 4; m = 7; λ = 6; tоб = 7,5. Определить:
а) вероятность того, что произвольный источник находится в активном состоянии
(коэффициент готовности);
б) среднее число простаивающих каналов;
в) среднее время ожидания заявки в очереди.
10.n = 3; m= 8; λ= 9; tоб = 4. Определить:
а) среднее число занятых каналов;
б) среднее время простоя канала;
в) вероятность того, что в СМО будет менее 6-ти заявок.
Формулы для вычислений
 -интенсивность потока заявок
-интенсивность потока заявок
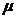 -интенсивность потока обслуживания
-интенсивность потока обслуживания
 - интенсивность нагрузки
- интенсивность нагрузки
T -интервал времени между двумя заявками (случайная величина)
 длина очереди (число мест)
длина очереди (число мест)
 количество заявок, поступающих в СМО
количество заявок, поступающих в СМО
Дата добавления: 2018-04-04; просмотров: 3040; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
