Удаление элемента с заданным номером
Чтобы удалить элемент с заданным номером (например, с номером k) нужно поставить указатель на элемент с номером k-1 и изменить его адресное поле, присвоив ему значение адреса элемента с номером k+1. Затем элемент с номером k удаляется с помощью функции delete (рис.).

Рис. 12. Удаление элемента из списка
//Удаление из однонаправленного списка элемента с номером k
point*del_point(point*beg,int k)
{
//поставить вспомогательную переменную на начало списка
point*p=beg;
point *r; //вспомогательная переменная для удаления
int i=0; //счетчик элементов в списке
if(k==0) //удалить первый элемент
{
beg=p->next;
delete p; //удалить элемент из списка
return beg; //вернуть адрес первого элемента
}
while(p)//пока нет конца списка
{
/*дошли до элемента с номером k-1, чтобы поменять его поле next*
if(i==k-1)
{
/*поставить r на удаляемый элемент
r=p->next;
if(r) //если p не последний элемент
{
p->next=r->next; //исключить r из списка
delete r; //удалить элемент из списка
}
/*если p -последний элемент, то в поле next присвоить 0*/
else p->next=0;
}
p=p->next; //переход к следующему элементу i++; //увеличить счетчик элементов
}
return beg;//вернуть адрес первого элемента
}
Удаление элемента с заданным ключом осуществляется аналогично, но вместо условия
if(i==k-1) //проверка номера
нужно использовать условие:
if(p->next->key==KEY)//проверка ключа,
|
|
|
где KEY заданный ключ. Ключ KEY передается как параметр функции удаления.
Добавление элемента с заданным номером
Для добавления в список элемента с номером k нужно поставить указатель на элемент с номером k-1. Затем нужно создать новый элемент и поменять значения адресных полей таким образом, чтобы адресное поле нового элемента содержало адрес элемента с номером k, а адресное поле k-1 элемента – адрес нового элемента (см. рис.).
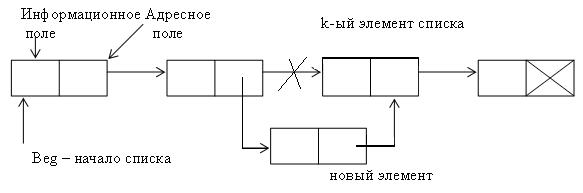
Рис. 13. Добавление элемента номером k
point* add_elem(point*beg, int NOM)
{
point*p=make_point();//создание нового элемента
if (NOM==0)//добавление первого элемента
{
p->next=beg;//связываем новый элемент со списком
beg=p;//меняем адрес beg
return beg;
}
point*r=beg;//указатель для перехода на нужный номер
/*проходим по списку до элемента с номером NOM-1 или до конца списка, если такого элемента нет */
for(int i=0; i<NOM-1&& r!=0;i++)
r=r->next;
//если элемента с указанным номером в списке нет
if (!r)
{
cout<<"\nNot such NOM!"; //сообщение об ошибке
return beg;
}
p->next=r->next;//связываем новый элемент со списком
//связываем элемент с номером NOM-1 с новым элементом
r->next=p;
return beg;
}
Двунаправленные списки
Двунаправленный список имеет два адресных поля, которые указывают на следующий элемент списка и на предыдущий. Поэтому двигаться по такому списку можно как слева направо, так и справа налево.
|
|
|

Рис. 14. Двунаправленный список
//пример описания двунаправленного списка
struct point //описание структуры
{
int key; //ключевое поле
//адресные поля
point* pred, //адрес предыдущего элемента
*next; // адрес следующего элемента
};
Ниже рассматривается программа, которая создает двунаправленный список, выполняет удаление элемента с заданным номером, добавление элемента с заданным номером и печать полученных списков
#include <iostream.h>
struct point //описание структуры
{
int key; //ключевое поле
point* pred,*next; //адресные поля
};
//формирование списка
point*make_list()
{
int n; //количество элементов списка
cout<<"n-?";
cin>>n;
point* p, *r, *beg;
p=new (point); //создать первый элемент
/*запомнить адрес в переменную beg, в которой хранится начало списка*/
beg=p;
cout<<"key-?";
cin>>p->key; //заполнить ключевое поле
p->pred=0;p->next=0; //запомнить адресные поля
//добавить элементы в конец списка
for(int i=1;i<n;i++)
{
r=new(point); //новый элемент
cout<<"key-?";
cin>>r->key; //адресное поле
|
|
|
p->next=r; //связать начало списка с r
r->pred=p; //связать r с началом списка
r->next=0; //обнулить последнее адресное поле
p=r; //передвинуть p на последний элемент списка
}
return beg;//вернуть первый элемент списка
}
//печать списка
void print_list(point *beg)
{
if (beg==0) //если список пустой
{
cout<<"The list is empty\n";
return;
}
point*p=beg;
while(p) //пока не конец списка
{
cout<<p->key<<"\t";
p=p->next; //перейти на следующий элемент
}
cout<<"\n";
}
//удаление элемента с номером k
point* del_point(point*beg, int k)
{
point *p=beg;
if(k==0)//удалить первый элемент
{
//переставить начало списка на следующий элемент
beg=beg->next;
//если в списке только один элемент
if(beg==0)return 0;
//если в списке более одного элемента
beg->pred=0;//обнулить адрес предыдущего элемента
delete p; //удалить первый
return beg; //вернуть начало списка
}
/*если удаляется элемент из середины списка, пройти по
списку либо до элемента с предыдущим номером, либо до конца списка*/
for(int i=0;i<k-1&&p!=0;i++,p=p->next);
//если в списке нет элемента с номером k
if(p==0||p->next==0)return beg;
//если в списке есть элемент с номером k
point*r=p->next; //встать на удаляемый элемент
p->next=r->next; //изменить ссылку
delete r; //удалить r
|
|
|
r=p->next; //встать на следующий
//если r существует, то связать элементы
if(r!=0)r->pred=p;
return beg; //вернуть начало списка
}
//добавить элемент с номером k
point* add_point(point *beg,int k)
{
point *p;
//создать новый элемент и заполнить ключевое поле
p=new(point);
cout<<"key-?";
cin>>p->key;
if(k==0)//если добавляется первый элемент
{
p->next=beg; //добавить перед beg
p->pred=0; //обнулить адрес предыдущего
//связать список с добавленным элементом
beg->pred=p;
beg=p; //запомнить первый элемент в beg
return beg; //вернуть начало списка
}
//если добавляется элемент середину или конец списка
point*r=beg; //встать на начало списка
/*пройти по списку либо до конца списка, либо до элемента с номером k-1*/
for(int i=0;i<k-1&&r->next!=0;i++,r=r->next);
p->next=r->next; //связать р с концом списка
//если элемент не последний, то связать конец списка с р
if(r->next!=0)r->next->pred=p;
p->pred=r; //связать р и r
r->next=p;
return beg; //вернуть начало списка
}
void main()
{
point*beg;
int i,k;
do
{
//печать меню
cout<<"1.Make list\n";
cout<<"2.Print list\n";
cout<<"3.Add point\n";
cout<<"4.Delete point\n";
cout<<"5.Exit\n";
cin>>i; //ввод выбранного пункта меню
switch(i)
{
case 1://формирование списка
{
beg=make_list();
break;
}
case 2://печать списка
{
print_list(beg);
break;
}
case 3://добавление элемента
{
cout<<"\nk-?";
cin>>k;
beg=add_point(beg,k);
break;
}
case 4://удаление элемента
{
cout<<"\nk-?";
cin>>k;
beg=del_point(beg,k);
break;
}
}
}
while(i!=5); //выход из программы
}
Очереди и стеки
Очередь и стек – это частные случаи однонаправленного списка.
В стеке добавление и удаление элементов осуществляются с одного конца, который называется вершиной стека. Поэтому для стека можно определить функции:
· top() – доступ к вершине стека (вывод значения последнего элемента
· pop() – удаление элемента из вершины (удаление последнего элемента);
· push() – добавление элемента в вершину (добавление в конец).
Такой принцип обслуживания называют LIFO (last in – first out, последний пришел, первый ушел).
point* pop(point*beg)
{
point*p=beg;
if (beg->next==0)//один элемент
{
delete beg;
return 0;
}
//ищем предпоследний элемент
while (p->next->next!=0)
p=p->next;
// ставим указатель r на последний элемент
point*r=p->next;
//обнуляем адресное поле предпоследнего элемента
p->next=0;
delete r; //удаляем последний элемент
return beg;
}
point* push(point* beg)
{
point*p=beg;// ставим указатель p на начало списка
point*q=new(point);// создаем новый элемент
cout<<"Key?";
cin>>q->data;
q->next=0;
if (beg==0)//список пустой
{
beg=q;//q становится первым элементом
return beg;
}
while (p->next!=0)//проходим до конца списка
p=p->next;
p->next=q; //связываем последний элемент с q
return beg;
}
В очереди добавление осуществляется в один конец, а удаление из другого конца. Такой принцип обслуживания называют FIFO (first in – first out, первый пришел, первый ушел). Для очереди также можно определить функции:
· front() – доступ к первому элементу;
· back() – доступ к последнему элементу;
· pop() – удаление элемента из конца;
· push() – добавление элемента в начало.
Бинарные деревья
Бинарное дерево - это динамическая структура данных, состоящая из узлов, каждый из которых содержит, кроме данных не более двух ссылок на другие бинарные деревья (поддеревья). На каждое поддерево имеется ровно одна ссылка (рис. )
Описать такую структуру можно следующим образом:
struct point
{
int data;//информационное поле
point* left;//адрес левого поддерева
point* right;//адрес правого поддерева
};
Начальный узел называется конем дерева. Узел, не имеющий поддеревьев, называется листом дерева. Исходящие листы называются предками, входящие – потомками. Высота дерева определяется количеством уровней, на которых располагаются узлы.
Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его правого поддерева - больше называется деревом поиска. Одинаковые ключи не допускаются. В дереве поиска можно найти элемент по ключу, двигаясь от корня и переходя на левое или правое поддерево в зависимости от значения в каждом узле. Такой поиск является более эффективным, чем поиск по линейному списку, т. к. время поиска определяется высотой дерева, а она пропорциональна двоичному логарифму количества узлов (аналогично бинарному поиску).
В идеально сбалансированном дереве количество узлов в справа и слева отличается не более, чем на единицу.
Линейный список можно представить как вырожденное бинарное дерево, в котором каждый узел имеет не более одной ссылки. Для списка среднее время поиска равно половине длины списка.
Деревья и списки являются рекурсивными структурами данных, т. к. каждое поддерево также является деревом. Дерево можно определить как рекурсивную структуру, в которой
каждый элемент является:
· либо пустой структурой;
· либо элементом, с которым связано конечное число поддеревьев.
Действия с рекурсивными структурами удобнее всего описываются с помощью рекурсивных алгоритмов.
Обход дерева
Для того, чтобы выполнить определенную операцию над всем узлами дерева, надо обойти все узлы. Такая задача называется обходом дерева. При обходе узлы должны посещаться в определенном порядке. Существуют три принципа упорядочивания, которые естественно вытекают из структуры дерева.
Рассмотрим следующее дерево.

Рис. 15. Структура бинарного дерева
На этом дереве можно определить три метода упорядочения:
· Слева направо: Левое поддерево – Корень – Правое поддерево;
· Сверху вниз: Корень – Левое поддерево – Правое поддерево;
· Снизу вверх: Левое поддерево – Правое поддерево – Корень.
Эти три метода можно сформулировать в виде рекурсивных алгоритмов. Эти алгоритмы служат примером того, что действия с рекурсивными структурами лучше всего описываются рекурсивными алгоритмами.
//Обход слева направо:
void Run(point*p)
{
if(p)
{
Run(p->left); //переход к левому п/д
<обработка p->data>
Run(p->right);//переход к правому п/д
}
}
Если в качестве операции обработки узла поставить операцию вывода информационного поля узла, то мы получим функцию для печати дерева.
Для дерева поиска на рис. обход слева направо даст следующие результаты:
1 3 5 7 8 9 12
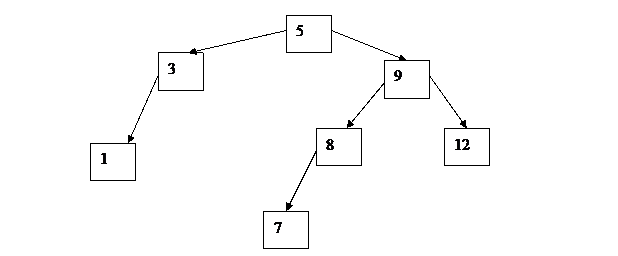
Рис. 16. Пример дерева поиска
//Обход сверху вниз:
void Run(point*p)
{
if(p)
{
<обработка p->data>
Run(p->left); //переход к левому п/д
Run(p->right);//переход к правому п/д
}
}
Результаты обхода слева направо для дерева поиска на рис. :
5 3 1 9 8 7 12
//Обход снизу вверх
void Run(point*p)
{
if(p)
{
Run(p->left); //переход к левому п/д
Run(p->right);//переход к правому п/д
<обработка p->data>
}
}
Результаты обхода сверху вниз для дерева поиска на рис. :
1 3 7 8 12 9 5
Формирование дерева
Рассмотрим построение идеально сбалансированного дерева. При построении такого дерева надо распределять узлы таким образом, чтобы количество узлов в левом и правом поддеревьях отличалось не более чем на единицу.
# include <iostream.h>
struct point
{
int data;
point*left,*right;
};
point* Tree(int n,point* p)
{
point*r;
int nl,nr;
if(n==0){p=NULL;return p;}
nl=n/2;//считаем количество узлов в левом поддереве
nr=n-nl-1; //считаем количество узлов в правом поддереве
r=new point;//создаем новый узел
cout<<"?";
cin>>r->data;//заполняем информационное поле
r->left=Tree(nl,r->left);//формируем левое поддерево
r->right=Tree(nr,r->right);//формируем правое поддерево
p=r;//связываем
return p;
}
//печать дерева
void Print(point*p, int l)
{
//обход слева направо
if(p)
{
Print(p->left,l+5);
for(int i=0;i<l;i++)cout<<" ";
cout<<p->data<<"\n";
Print(p->right,l+5);
}
}
void main()
{
point*root;
root=Tree(10,root);
Print(root,1);
}
Функция печати, которая используется в данной программе, печатает дерево по уровням слева направо. Переменная l считает количество пробелов, которые надо отступить для печати следующего уровня. Результат работы программы представлен на рис.17.

Рис. 17. Результат работы программы формирования и печати дерева поиска
При формировании дерева поиска нужно учитывать упорядоченность элементов в таком дереве, т. е. добавление элемента с ключом больше текущего осуществляется в правое поддерево, а меньше текущего – в левое. Ключи не дублируется, поэтому необходимо проверить существует ли элемент с заданным ключом в дереве и если существует, то завершить функцию добавления элемента.
point* first(int d)//формирование первого элемента дерева
{
point* p=new point;
p->key=d;
p->left=0;
p->right=0;
return p;
}
//добавление элемента d в дерево поиска
Point* Add(point*root,int d)
{
Point*p=root,*r;
// флаг для проверки существования элемента d
bool ok=false;
while(p&&!ok)
{
r=p;
if(d==p->key)ok=true;
else
if(d<p->key)p=p->left;//пойти в левое поддерево
else p=p->right;//пойти в правое поддерево
}
if(ok) return p;//найдено, не добавляем
//создаем узел
point* q=new point();//выделили память
q->key=d;
q->left=0;
q->right=0;
//добавляем в левое поддерево
if(d<r->key)r->left=q;
//добавляем в правое поддерево
else r->right =q;
return q;
}
Удаление элемента из дерева
Рассмотрим удаление элемента из дерева поиска (рис. 16). Следует учитывать следующие случаи:
1. Узла с требуемым ключом в дереве нет.
2. Узел с требуемым ключом является листом, т. е. не имеет потомков.
3. Узел с требуемым ключом имеет одного потомка.
4. Узел с требуемым ключом имеет двух потомков.
В первом случае необходимо выполнить обход дерева и сравнить ключи элементов с заданным значением.
Во втором случае нужно заменить адрес удаляемого элемента нулевым. Для этого нужно выполнить обход дерева и заменить адрес удаляемого элемента нулевым. Например, при удалении элемента с ключом 7 мы меняем левое адресное поле элемента с ключом 8 на 0.
Третий случай похож на второй, т. к. мы должны заменить адресное поле удаляемого элемента адресом его потомка. Например, при удалении элемента с ключом 8 мы меняем левое адресное поле элемента с ключом 9 на адрес элемента с ключом 7.
Самым сложным является четвертый случай, т .к. возникает вопрос каким элементом мы должны заменить удаляемый элемент. Этот элемент должен иметь два свойства. Во-первых, он должен иметь не более одного потомка, а во-вторых, мы должны сохранить упорядоченность ключей, т. е. он должен иметь ключ либо не меньший, чем любой ключ левого поддерева удаляемого узла, либо не больший, чем любой ключ правого поддерева удаляемого узла. Таким свойством обладают два узла: самый правый узел левого поддерева удаляемого узла и самый левый узел правого поддерева удаляемого узла. Любым из них и можно заменить удаляемый элемент. Например, при удалении узла 9 его можно заменить узлом 12 (самый левый узел правого поддерева удаляемого узла).
Для удаления будем использовать рекурсивную функцию.
/*вспомогательная переменная для удаления узла, имеющего двух потомков*/
point *q;
Point* Del(Point* r)
{
/*удаляет узел, имеющий двух потомков, заменяя его правым узлом левого поддерева*/
if (r->right!=0) r=Del(r->right);//идем в правое поддерево
else //дошли до самого правого узла
{
//заменяем этим узлом удаляемый
q->key=r->key;
q=r;
r=r->left;
}
return r;
}
Point* Delete(Point*p, int KEY)
{
//Point*q;
if(p) //ищем узел
if (KEY<p->key)//искать в левом поддереве
p->left=Delete(p->left,KEY);
else if (KEY>p->key)//искать в правом поддереве
p->right=Delete(p->right,KEY);
else //узел найден
{
//удаление
q=p;//запомнили адрес удаляемого узла
// узел имеет не более одного потомка слева
if(q->right==0)
p=q->left;//меняем на потомка
else
//узел имеет не более одного потомка справа
if(q->left==0)
p=q->right;//меняем на потомка
else //узел имеет двух потомков
p->left=Del(q->left);
delete q;
}
return p;
}
Дата добавления: 2018-04-04; просмотров: 1085; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
