Средние величины, определение, применение
Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени, т.е. средняя величина позволяет одним числом количественно охарактеризовать качественно однородную совокупность.
Средние величины рассчитывают на основании вариационных рядов, достаточного числа наблюдений и однородных статистических групп.
Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте.
К средним величинам предъявляются следующие требования:
– средняя должна характеризовать качественно однородную совокупность;
– средние должны исчисляться по данным большого числа единиц, составляющих совокупность, то есть отображать массовые социально-экономические явления.
Средние величины применяются:
· для оценки состояния здоровья — например, параметров физического развития (средний рост, средняя масса тела, среднее значение жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средняя величина пульса, средняя СОЭ и др.);
|
|
|
· для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений на 1 час приема в поликлинике и др.);
· для оценки состояния окружающей среды
Средние величины получаются из рядов распределения (вариационных рядов). В таком ряду количественно изменяющийся признак носит название варьирующего, а отдельные его количественные выражения называются вариантами (V). Числа, показывающие, как часто встречается та или иная варианта в составе данного ряда, носят название частот (P).
Полученные при исследовании одного и того же признака у единиц наблюдения статистической совокупности абсолютные величины сначала записывают в том порядке, как их получает исследователь, т.е. хаотично.
Виды средних величин. Виды. Виды средней арифметической.
Различают несколько видов средних величин: мода, медиана, средняя арифметическая, средняя геометрическая, средняя гармоническая и т.д.
Модой ( Мо) называется та варианта, которой соответствует наибольшее количество частот вариационного ряда.
|
|
|
В санитарной статистике применение моды довольно ограничено. Модой можно пользоваться для оценки средней длительности заболеваний, особенно при малом количестве больных данной болезнью.
Медианой (Ме) называется варианта, делящая вариационный ряд на две равные половины и расположенная в середине вариационного ряда, т.е. величина признака, занимающего в вариационном ряду срединное положение, если ряд нечетный, и если ряд четный, то определяется как полусумма двух средних вариант. Для определения медианы надо найти середину ряда. При четном числе наблюдений за медиану принимают среднюю величину из двух центральных вариант. При нечетном числе наблюдений медианой будет серединная (центральная) варианта.
Медиана применяется в санитарной статистике относительно редко.
Основным отличием медианы и моды от средней арифметической является то, что на их размеры не оказывают влияния величина крайних значений вариант, имеющихся в вариационном ряду, тогда как при определении средней арифметической принимаются во внимание значения всех вариант.
Определение и применение средней арифметической в
Здравоохранении. Способы расчета средней арифметической.
Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.
|
|
|
Наиболее часто в характеристике вариационного ряда используют среднюю арифметическую.
Различают три вида средней арифметической: простая, взвешенная и вычисленная по способу моментов. Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только 1 раз называется средней арифметической простой. Ее определяют по формуле:
M= 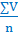 ,
,
где М – средняя арифметическая,
V – варианта изучаемого признака,
n–число наблюдений.
Если в исследуемом ряду одна или несколько вариант повторяются несколько раз, то вычисляют среднюю арифметическую взвешенную, когда учитывается вес каждой варианты в зависимости от частоты ее встречаемости. Расчет такой средней проводят по формуле:
M=  ,
,
где М – средняя арифметическая взвешенная;
∑ - знак суммы;
V – варианты (числовые значения изучаемого признака);
P – частота, с которой встречается одна и та же варианта признака, т.е. сумма вариант с данным значением признака;
n – число наблюдений, т.е., сумма всех частот или общее число всех вариант (∑p).
В случаях, когда варианты представлены большими числами (например, масса тела новорожденных в граммах) и имеется число наблюдений, выраженное сотнями или тысячами случаев, взвешенная средняя арифметическая может быть вычислена по способу моментов по формуле:
|
|
|
M = A + 
где A – условно взятая средняя величина (чаще всего в качестве условной средней берется Мо);
∑ - знак суммы;
α – отклонение каждой варианты в интервалах от условной средней
p – частота (число раз, с которым встречается одна и та же варианта признака).
αp – произведение отклонения (α) на частоту (p);
n – число наблюдений, т.е. сумма всех частот или общее число всех вариант (∑p);
i – величина интервала.
Средняя арифметическая (средняя взвешенная) имеет ряд свойств, которые используют в некоторых случаях для упрощения расчета средней и получения ориентировочной величины.
1. Средняя арифметическая занимает срединное положение в строго симметричном вариационном ряду.
2. Средняя арифметическая имеет абстрактный характер и является обобщающей величиной, выявляющей закономерность.
3. Алгебраическая сумма отклонений всех вариант от средней равна нулю: ∑ (V - M) = 0. На этом свойстве основан расчет средней по способу моментов.
Дата добавления: 2018-04-04; просмотров: 883; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
