Условия однозначности для теплопроводности
Ответ на теоретический вопрос.
Выведите дифференциальное уравнение теплопроводности для
однородного изотропного тела. Что такое коэффициент температуропроводности, какова его размерность?
Изучение любого физического явления сводится к установлению зависимости между величинами, характеризующими это явление. Для сложных физических процессов, в которых определяющие величины могут существенно изменяться в пространстве и времени, установить зависимость между этими величинами достаточно сложно. В таких случаях используют методы математической физики, которые заключаются в том, что ограничивается промежуток времени и из всего пространства рассматривается некоторый элементарный объем. Это позволяет в пределах выбранного объема и данного промежутка времени пренебречь изменениями величин, характеризующих процесс, и существенно упростить зависимость.
Выбранные таким образом элементарный объем dVи элементарный промежуток времениdτ, в пределах которых рассматривается процесс, с математической точки зрения являются величинами бесконечно малыми, а с физической точки зрения – величинами еще достаточно большими, чтобы в их пределах можно было считать среду как сплошную, пренебрегая ее дискретным строением. Полученная таким образом зависимость является общим дифференциальным уравнением процесса. Интегрируя дифференциальные уравнения, можно получить аналитическую зависимость между величинами для всей области интегрирования и всего рассматриваемого промежутка времени.
|
|
|
Для решения задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности.
Примем следующие допущения:
· тело однородно и изотропно;
· физические параметры постоянны;
· деформация рассматриваемого объема, связанная с изменением температуры, очень мала по сравнению с самим объемом;
· внутренние источники теплоты в теле, распределены равномерно.
В основу вывода дифференциального уравнения теплопроводности положим закон сохранения энергии, который сформулируем так:
Количество теплоты dQ, введенное в элементарныйобъемdVизвне за времяdτвследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества, содержащегося в элементарном объеме.
где dQ1– количество теплоты, введенное в элементарныйобъемdVпутем теплопроводности за времяdτ;
dQ2– количество теплоты, которое за времяdτвыделилось в элементарномобъемеdVза счет внутренних источников;
dQ– изменение внутренней энергии (изохорный процесс) или энтальпии вещества (изобарный процесс), содержащегося в элементарномобъемеdVзавремяdτ.
|
|
|
Для получения уравнения рассмотрим элементарный объем в виде кубика со сторонамиdx, dy, dz (см. рис.1.2.). Кубик расположен так, чтобы его грани были параллельны соответствующим координатным плоскостям. Количество теплоты, которое подводится к граням элементарного объема за времяdτв направлении осейx, y, z обозначим соответственноdQx, dQy,dQz.
Количество теплоты, которое будет отводиться через противоположные грани в тех же направлениях, обозначим соответственно dQx+dx, dQy+dy,dQz+dz.
Количество теплоты, подведенное к грани dxdy в направлении оси x за время dτ, составляет: 
где qx– проекция плотности теплового потока на направление нормали к указанной грани. Соответственно количество теплоты, отведенное через противоположную грань будет:
Разница между количеством теплоты, подведенном к элементарному объему, и количеством теплоты, отведенного от него, представляет собой теплоту: 
Функция q является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора:
Если ограничиться двумя первыми слагаемыми ряда, то уравнение запишется в виде: 
Аналогичным образом можно найти количество теплоты, подводимое к объему в направлении двух других координатных осей y иz.
|
|
|
Количество теплоты dQ, подведенное в результате теплопроводности к рассматриваемому объему, будет равно:
Второе слагаемое определим, обозначив количество теплоты, выделяемое внутренними источниками в единице объема среды в единицу времени qvи назовем егомощностью внутренних источников теплоты [Вт/м3], тогда:
Третья составляющая в нашем уравнении найдется в зависимости от характера ТД процесса изменения системы.
При рассмотрении изохорного процесса вся теплота, подведенная к элементарному объему, уйдет на изменение внутренней энергии вещества, заключенного в этом объеме, т.е. dQ=dU.
Если рассматривать внутреннюю энергию единицы объема u=f(t,v), то можно записать:
,Дж/м3
,Дж/кг
где cv – изохорная теплоемкость или единицы объема или единицы массы, [Дж/м3];
ρ– плотность,[кг/м3].
Соберем полученные выражения:
Полученное выражение является дифференциальным уравнением энергии для изохорного процесса переноса теплоты.
Аналогично выводится уравнение для изобарного процесса. Вся теплота, подведенная к объему уйдет на изменение энтальпии вещества, заключенного в объеме.
|
|
|
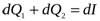
Полученное соотношение является дифференциальным уравнением энергии для изобарного процесса.
В твердых телах перенос теплоты осуществляется по закону Фурье 
,значение теплоемкости можно принять 
. Напомним, что проекция вектора плотности теплового потока на координатные оси определяются выражениями:
Последнее выражение называют дифференциальным уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменениями температуры в любой точке тела, в котором происходит процесс теплопроводности.
Наиболее общее дифференциальное уравнение теплопроводности в частных производных имеет такую же форму, но в нем величины ρ,l,сявляются функциями времени и пространства. Это уравнение описывает большое количество задач теплопроводности, представляющих практический интерес. Если принять теплофизические параметры постоянными, то уравнение будет проще:
Обозначим 
, тогда:
Коэффициент пропорциональности а [м2/с] называется коэффициентом температуропроводности и является физическим параметром вещества. Он существенен для нестационарных тепловых процессов характеризует скорость изменения температуры. Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности является мерой теплоинерционных свойств тела. Например, жидкости и газы обладают большей тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности, а металлы наоборот имеют малую тепловую инерционность.
Далее, если система тел не содержит внутренних источников теплоты q=0, тогда дифференциальное уравнение принимает форму уравнения Фурье:
Если имеются внутренние источники теплоты, а температурное поле является стационарным, то мы получаем уравнение Пуассона:
Наконец, при стационарной теплопроводности и отсутствии внутренних источников теплоты мы получаем уравнение Лапласа:
Условия однозначности для теплопроводности.
Так как дифференциальное уравнение теплопроводности выведено из общих законов физики, то оно описывает целый класс явлений. Для его решения необходимо задать граничные условия или условия однозначности.
Условия однозначности включают:
1. геометрические условия – характеризуют форму и размеры тела;
2. физические условия – характеризуют физические свойства среды и тела;
3. начальные (временные) условия – характеризуют распределение температур в теле в начальный момент времени, задаются при исследовании нестационарных процессов;
4. граничные условия – характеризуют взаимодействие рассматриваемого тела с окружающей средой.
Граничные условия могут быть заданы несколькими способами.
Граничные условия первого рода.Задается распределение температуры на поверхности тела для каждого момента времени:
tc=f(x,y,z,τ)
где tc– температура на поверхности тела;
x,y,z– координаты поверхности тела.
В частном случае, когда температура на поверхности является постоянной на протяжении всего времени протекания процессов теплообмена, уравнение упрощается:
tc=const
Граничные условия второго рода. Задаются значения теплового потока для каждой точки поверхности тела и любого момента времени. Аналитически выглядит так:
qc=f(x,y,z,τ)
В простейшем случае плотность теплового потока по поверхности тела остается постоянной. Такой случай имеет место при нагревании металлических изделий в высокотемпературных печах.
Граничные условия третьего рода.При этом задаются температура окружающей средыtсри закон теплообмена между поверхностью тела и средой. Для описания процесса теплообмена используется закон Ньютона-Рихмана. Согласно этому закону количество теплоты, отдаваемое или принимаемое единицей поверхности тела в единицу времени, пропорционально разности температур поверхности тела и среды:
где α коэффициент пропорциональности, называется коэффициентом теплоотдачи [Вт/(м2·К)], характеризует интенсивность теплообмена. Численно он равен количеству теплоты, отдаваемому единицей поверхности тела в единицу времени при разности температур равной одному градусу. Согласно закону сохранения энергии количество теплоты, которое отводится окружающей среде, должно равняться теплу, подводимому вследствие теплопроводности из внутренних частей тела, то есть:
Последнее уравнение является граничным условием третьего рода.
Встречаются более сложные технические задачи, когда ни одно из перечисленных условий задать невозможно, и тогда приходится решать задачу методом сопряжения. При решении такой задачи должны выполняться условия равенства температур и тепловых потоков по обе стороны от границы раздела. В общем случае условия сопряженности можно записать:
Решение сопряженной задачи связано с нахождением температурных полей по обе стороны границы раздела.
Задача.На токарном станке модели 16К20 обтачивается заготовка из Серого чугуна СЧ20, 
резцом с пластинкой твердого сплава ВК8 с передним углом 
и углом в плане 
. Глубина резания t=5 мм, подача s=0,87 мм/об, скорость резания u=75 м/мин.
Определить:
- мощность тепловыделения в зоне резания Q;
- эквивалентную теплопроводность державки с пластиной по нормали к основанию резца;
- рассчитать температуру на опорной поверхности пластинки инструментального материала со стороны задней грани, исходя из предположения, что в резец идет 5 % общего количества тепла.
Температуру разупрочнения считать равной 250 °С
1. Общее количество теплоты, выделяющейся при резании можно определить по формуле [1]:
где Pz - тангенциальная составляющая усилия резания;
- скорость резания, м/мин.
Составляющая усилия резания Pz может быть вычислена по формуле [5]:
,
где 
- поправочные коэффициенты
Ср=92, х=1,0, у=0.75, n=0 [5, с.273]
[5, с.271] 
[5, с.264]
Kp=8∙0,94∙1∙1,1=8,272
Pz=10∙92∙ 
∙ 
∙8,272=45040H=450кг
В этом случае в зоне резания выделяется
Q = 0,039∙450∙75 =1316 кал/с = 1.51Вт
2. Для определения эквивалентной теплопроводности державки с пластиной режущей части можно воспользоваться формулой
где h - высота пластинки, см; принимаем H=4мм=0,4см.;
Н - высота державки, см; принимаем Н=25мм=2,5 см;
- теплопроводность материала режущей пластинки; принимаем из приложения Г для ВК8 =0,13 кал/( 
);
- теплопроводность материала державки; принимаем из приложения Г для стали 40 =0,092 кал/( ).
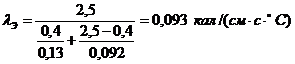Тогда
3. Для расчета температуры в основании пластинки можно воспользоваться формулой
 |
где q - интенсивность тепловыделения в тело резца на единицу длины режущей кромки,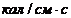 
;
- интегрально-показательная функция;
r - расстояние от режущей кромки до опорной плоскости пластинки, мм;
- коэффициент температуропроводности, 
;
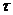- время обработки одной детали, с;
Интенсивность тепловыделения q можно определить по формуле q=0.05 Q/b
где b - длина активной части режущей кромки, см:
Тогда
Для определения времени обработки зададимся длиной обрабатываемой детали L=25 мм и диаметром 
120 мм. В этом случае частота вращения детали будет равна
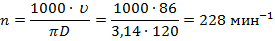Время обработки одной детали составит
Коэффициент температуропроводности 
принимаем из приложения Г равным 0,246 .
Аргумент интегрально показательной функции равен
,
а сама функция равна
.
Температура на основании пластинки равна
Вывод: температура на основании пластины больше температуры разупрочнения материала державки, следует уменьшить режим резания, применить СОЖ.
СПИСОК ИСПОЛЬЗОВАННЫХ ЛИТЕРАТУРНЫХ ИСТОЧНИКОВ
1. Резников А. Н., Резников Л. А. Тепловые процессы в технологических системах. – М.: Машиностроение, 1990. – 228 с.
2. Ящерицын П. И. Теория резания: учебник / П. И. Ящерицын,
Е. Э. Фельдштейн, М. А. Корниевич. – Минск: Новое знание, 2005. – 512 с.
3. Попок Н. Н. Теория резания: учеб.-метод. комплекс для студентов
машиностроительных специальностей / Н. Н. Попок. – Новополоцк: ПГУ,
2005. – 240 с.
4. Попок Н. Н. Теория резания: учеб.пособие для студентов машиностроительных специальностей / Н. Н. Попок. – Новополоцк: ПГУ,
2006. – 228 с.
5. Справочник технолога-машиностроителя в 2-х томах. Т. 2. / под
ред. А. Г. Косиловой и Р. К. Мещерякова. – 4-е изд., перераб. и доп. – М.: Машиностроение, 1985. – 240 с.
Дата добавления: 2018-04-04; просмотров: 771; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!