Применение ЭВМ в тепловых расчетах

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Самарский государственный технический университет» (ФГБОУ ВПО «СамГТУ»)   Кафедра «Теоретические основы теплотехники и гидромеханика»    

ПРИМЕНЕНИЕ ЭВМ

В

ТЕПЛОВЫХ РАСЧЕТАХ

 

Лабораторный практикум

 

направление подготовки – 140100 «Теплоэнергетика и теплотехника»

профиль подготовки – «Тепловые электрические станции»

«Энергообеспечение предприятий»

«Промышленная теплоэнергетика»

«Энергетика теплотехнологий»

 

Самара

2015

Лабораторная работа №1

«Численное решение двумерных задач стационарной теплопроводности методом итераций»

Цель работы - приобретение навыков расчета двумерных задач стационарной теплопроводности методом конечных разностей (методомсеток) и методом итераций.

В настоящее время существует много различных приближенных методов расчета теплопроводности, которые приводят к удовлетворительным для инженерной практики результатам. Приближенные методы решения задач применяются в случае, когда точные аналитические методы расчета затруднительны. Одним из приближенных методов и является численный метод – метод конечных разностей или метод сеток.

На практике часто интересуются распределением температур в двухмерных областях, т.е. когда температура изменяется только по двум координатам (например, угол здания, угол промышленной печи, изгиб детали, заготовки и т.д.). Знание такого распределения температур может помочь определить температурные напряжения, тепловые потоки.

Изложение численного метода

Из численных методов наибольшее распространение для решения задач теплопроводности получил метод конечных разностей (или, иначе, методсеток). Его основная идея – это перевести дифференциальное уравнение в частных производных (в нашем случае это уравнение Лапласа) в алгебраические уравнения с заменой дифференциалов на конечные разности.

Алгоритм применения метода сеток для приближенного решения двумерных краевых задач стационарной теплопроводности заключается в следующем:

1. В плоской области L, в которой разыскивается решение, строится сеточная область L^’, состоящая из одинаковых ячеек и приближающая заданную область (рис.1.). На пересечении линий, составляющих сетку, образуются так называемые узлы сетки i, j.

2. Заданное дифференциальное уравнение в частных производных – уравнение Лапласа

,                                              (1)

которое описывает процесс стационарной теплопроводности, заменяется в каждом из внутренних узлов сетки, так называемым, конечно-разностным уравнением (см. ниже). Конечно-разностное уравнение представляет собой алгебраическое уравнение, связывающее значения температур в соседних узлах сетки.

Таким образом, дифференциальное уравнение (1) заменяется целой системой большого числа алгебраических уравнений.

3. На основании известных граничных условий на контуре M области L (например, при решении задач с граничными условиями 1-го рода) устанавливаются значения искомого решения в граничных узлах области L^’, т.е. на контуре M^’.

4. Значения во внутренних узлах области L^’ находятся путем решения указанной системы алгебраических уравнений. На этом и заканчивается, в принципе, построение метода сеток.

Для решения систем алгебраических уравнений имеется большое число различных методов. Далее мы будем использовать здесь метод итераций.

Остановимся теперь подробнее на описании метода сеток. Для получения сеточной области L^’ на заданную область Lнаносится сетка, состоящая из 2-х систем взаимно перпендикулярных прямых, отстоящих друг от друга на расстоянии h. Это расстояние h называется шагом сетки, выбор которого определяется требованиями расчета температурного поля двумерной области.

Контур M^’ области L^’ выбирается так, чтобы он был как можно ближе к контуру М области L.

В каждый из граничных узлов контура M^’ задаются граничные значения, равные известным значениям точки контура М, ближайшей к данному узлу.

 

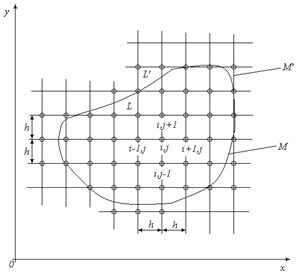
Рис.1. Сеточная область двумерной задачи стационарной теплопроводности

 

Пусть температура вдоль оси х меняется так, как показано на рис.2.

Рис.2. Схема определения разностных производных

 

Производную от t по x в узле i, j можно приближенно заменить на конечно-разностные соотношения следующими способами:

1)  - разностная производная «вперед» для узла i, j;

2)  - центральная разностная производная;

3)  - разностная производная «назад» для узла i, j.

Вторую производную, очевидно, можно приближенно получить в виде

 

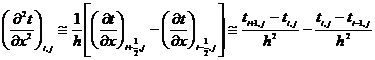
.                                (2)

Аналогичным образом запишем вторую производную по оси y

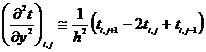.                     (3)

Тогда уравнение (1) в конечных разностях будет иметь вид

                    (4)

или

,                            (5)

т.е. t_i,j в узле i, j является среднеарифметическим значением температур в соседних узлах.

Такое уравнение может быть записано для каждой узловой точки i, j внутри области L^’.

Записав уравнение вида (4) для всех точек внутренней сеточной области L^’, заменим дифференциальное уравнение (1) целой системой линейных алгебраических уравнений типа (4).

Если внутренних точек области L^’ было N, то получится система из Nлинейных алгебраических уравнений с N неизвестными. Решение этой системы уравнений может быть проведено методом итераций.

Метод итераций заключается в следующем:

1) во всех внутренних точках области L^’ задаются произвольные значения температур t_i,j – эту систему значений обозначают системой №1;

2) во всех внутренних точках области L^’ образуются в соответствии с (5) среднеарифметические значения системы №1, полученную систему обозначают №2 (граничные значения температур на контуре всегда остаются заданными);

3) из системы №2 аналогичным образом получается система №3 и т.д.

Процесс итераций считается законченным тогда, когда в пределах заранее заданной точности система № (n+1) совпадает с системой № n.

В курсах высшей математики показывается, что описанный процесс итераций в данном случае будет сходиться к решению дифференциального уравнения Лапласа (1) с заданными условиями.

 

Постановка задачи

Найти температурное поле в углу печи (здания) (рис.3), используя метод конечных разностей, если на поверхностях ДС и ДЕ задана температура t_w2, на поверхностях АВ и АF – температура t_w1. На ВС и FE имеют место линейные законы распределения температур.

Расчет на ЭВМ производить с точностью δt. Результаты решения представить в виде сетки изотерм с шагом Δt. Построить графики распределения температур в двух сечениях исследуемой области (по указанию преподавателя).

Рис.3. Сеточная область угла здания

Числовые значения температур и размеров области взять из табл.1.

Таблица 1

Номер варианта	l1, мм	l2, мм	tw1, oC	tw2, oC	Заданная точность расчета, oC
1	320	160	20	-20	0,1
2	200	100	80	0	0,2
3	100	50	500	50	1,0
4	160	80	30	-10	0,1
5	120	60	200	20	1,0
6	200	100	100	20	0,8
7	400	200	800	0	1,5
8	80	40	220	20	2,5
9	100	50	30	-20	0,4
10	600	300	1000	0	2
11	120	60	100	10	1,0
12	400	200	25	-25	0,5
13	240	120	20	-15	0,5
14	160	80	150	25	0,2
15	200	100	20	-10	0,3
16	240	120	500	50	0,4
17	160	80	100	10	0,5
18	400	200	700	70	0,4
19	80	40	10	-20	0,2
20	320	160	20	0	0,3
21	120	60	120	20	0,4
22	100	50	5	25	0,5
23	140	70	-20	20	0,1
24	500	250	600	100	2
25	300	150	100	0	0,3

 

Содержание отчета

1. Расчет температурного поля методом итераций (ручной счет двух итераций) с необходимыми пояснениями.

2. Результаты расчета температурного поля на ЭВМ.

3. Графическое представление результатов расчета в виде сетки изотерм.

Контрольные вопросы

1. Приведите примеры двумерных стационарных температурных полей.

2. Что значит двумерное температурное поле?

3. Объяснить термин «стационарное температурное поле».

4. В чем заключается идея метода итераций?

5. Когда процесс итераций можно завершить?

6. Как определялись граничные условия на торцах угла здания (печи)?

7. В чем заключается основная идея метода конечных разностей?

 

Лабораторная работа №2

«Численное решение одномерных задач нестационарной теплопроводности методом конечных разностей по явной схеме»

Цель работы: приобретение навыков расчета одномерных задач нестационарной теплопроводности методом конечных разностей по явной схеме.

 

На практике часто встречаются случаи, когда изменение температуры происходит только по одной координате (направлению) и по времени. Например, охлаждение или нагревание плоской неограниченной пластины; стержня, изолированного с боковой поверхности и др. Интерес представляет знание температуры в любой точке такого тела в любой момент времени. Одним из наиболее простых методов решения таких одномерных задач нестационарной теплопроводности является метод конечных разностей, реализуемый по, так называемой, явной схеме, т.е. когда температуру для последующего момента времени можно выразить через температуры для предыдущего момента времени, причем по очень простой формуле.

 

Изложение численного метода

Дифференциальное уравнение нестационарной теплопроводности в случае одномерной задачи имеет вид

.                                                          (6)

Для численного решения этого уравнения воспользуемся методом конечных разностей или методом сеток.

В соответствии с этим методом на пространственно-временную область АВСD одномерной задачи (рис.4) наносится сеточная область с шагом сетки по оси х - ∆х и по времени τ - ∆τ.

Рис.4. Пространственно-временная область

одномерной задачи теплопроводности

 

Затем уравнение (6) заменяют конечно-разностной аппроксимацией (приближением), которое может быть проведено по различным схемам.

Для уравнения теплопроводности различают два типа разностных схем: явнуюинеявную.

Явную схему мы получим, если возьмем разностное представление производной по времени в (6) «вперед»

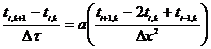.                                      (7)

(Здесь выражение для второй производной по координате также представлено конечно-разностной аппроксимацией . (см. лабораторную работу №1)).

Отсюда

.                                   (8)

В частности, при

                                                                (9)

формула (3) приобретает особенно простой вид

,                                              (10)

т.е. температура в данном узле для момента времени k+1 равна среднеарифметическому из значений температур в соседних узлах для момента времени k.

Из формул (8) и (10) видно, что температура для последующего момента времени k+1 явным образом выражается через температуры для предыдущего момента времени k, поэтому схема и называется явной.

Таким образом, начиная с какого-то начального момента времени k, можно последовательно вычислить все температуры для моментов k+1, k+2, k+3,…,k+n.

Исследования показали, что явная схема будет устойчивой, т.е. ошибки неточного задания краевых условий и округления не будут возрастать при увеличении τ, если выполняется условие

,                                                   (11)

откуда

.                                                  (12)

 

Постановка задачи

 

Найти температурное поле в теплоизолированном с боковой поверхности ограниченном стержне,разделенным на  частей, при следующих краевых условиях:

1) в начальный момент времени τ=0, t=t₀;

2) при х=0, t=t_w1=const;

3) при х=l, где l– длина стержня, t=t_w2=const.

Числовые значения исходных данных взять из табл.2.

 

Внимание!Шаг по времени должен быть обязательно меньше рассчитанногопо формуле:

,

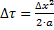где  – шаг по координате.

 

 

Таблица 2

Номер варианта	Материал	l, м	t0, oC	tw1, oC	tw2, oC	Физические свойства материала
						λ, Вт/(м·гр)	Ср, Дж/(кг·гр)	ρ, кг/м3
1	Асбест распушенный, 3 сорт	0,02	10	30	300	0,087	816	340
2	Асбест распушенный, 6 сорт	0,05	10	20	200	0,11	816	650
3	Асбестовый картон	0,02	20	50	140	0,16	816	900
4	Асбестовый шнур	0,025	20	100	100	0,13	816	800
5	Бетон с каменным щебнем	0,05	30	0	20	1,28	840	2000
6	Железобетон набивной	0,04	20	100	20	1,55	840	2200
7	Асфальт	0,01	20	50	20	0,7	1670	2120
8	Шлакобетон	0,36	20	50	50	0,7	800	1500
9	Гипс сухой	0,012	200	0	200	0,43	900	1250
10	Глина	0,02	300	20	20	0,9	840	2000
11	Глина огнеупорная	0,01	450	100	150	1,04	1090	1845
12	Дерево – дуб поперек волокон	0,2	10	30	30	0,2	2390	825
13	Дерево – дуб вдоль волокон	0,02	10	50	50	0,4	2390	819
14	Дерево – сосна поперек волокон	0,02	0	50	50	0,15	2720	546
15	Кирпич красный ручной формовки	0,06	150	150	0	0,7	880	1800
16	Кирпич красный машинной формовки	0,06	20	200	200	0,77	880	1700
17	Кирпич силикатный	0,02	10	300	10	0,81	840	1900
18	Мел	0,01	20	80	80	0,9	880	2000
19	Резина твердая	0,03	10	60	10	0,16	1380	1200
20	Стекло зеркальное	0,03	400	400	80	0,8	779	2550

 

 

Содержание отчета

 

1. Расчет температурного поля для двух моментов времени с необходимыми пояснениями по явной схеме.

2. Результаты расчета температурного поля на ЭВМ.

3. Графическое представление результатов расчета.

 

Контрольные вопросы

 

1. Приведите примеры одномерного нестационарного температурного поля.

2. В чем основная идея метода конечных разностей?

3. Почему схема расчета называется «явная»?

4. Укажите преимущества и недостатки явной схемы.

5. Почему явная схема считается неустойчивой?

6. Как определяется коэффициент температуропроводности?

7. Поясните, каким образом производится замена дифференциального уравнения теплопроводности на конечно-разностное уравнение по явной схеме.

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Основная литература

1. Кудинов А.А. Тепломассообмен. М.: ИНФРА-М, 2012. 375 с. (Высшее образование).

2. Техническая термодинамика и теплопередача [Текст] : учеб. / В. А. Кудинов, Э. М. Карташов, Е. В. Стефанюк. - М. : Юрайт, 2011. - 560 с. : граф., схем.

3. Техническая термодинамика и теплопередача [Текст] : учеб.пособие / В. В. Нащокин. - 4-е изд., стер. - М. : Аз-book, 2009. - 469 с. : граф.

 

Дополнительная литература

4. Теплопроводность и термоупругость в многослойных конструкциях: учеб.пособие / В.А.Кудинов, Б.В.Аверин, Е.В.Стефанюк. – М.: Высш.шк., 2008. -305 с.: ил.

5. Теплотехника: учеб.пособие / В.А.Кудинов, Э.М.Карташов, Е.В.Стефанюк. – Самар.гос.техн.ун-т, 2008. -471 с.: ил.Аналитические решения задач тепломассопереноса и термоупругости для многослойных конструкций [Текст] : учеб.пособие / В.А.Кудинов,Э.М.Карташов,В.В.Калашников. - М. : Высш.шк., 2005. - 430 с. : ил.,табл.

6. Теплопроводность и термоупругость в многослойных конструкциях [Текст] : учеб. пособие / В. А. Кудинов, Б. В. Аверин, Е. В. Стефанюк ; ред. Э. М. Карташов ; Самар.гос.техн.ун-т. - Самара : [б. и.], 2008. - 391 с. : граф., табл.

7. Справочник по теплофизическим свойствам газов и жидкостей [Текст] / Н. Б. Варгафтик. - 3-е изд.,стер.ииспр. - М. :Старс, 2006. - 720 с. (100 экз.)

8. Энергосбережение в теплоэнергетике и теплотехнологиях [Текст] / А. А. Кудинов, С. К. Зиганшина. - М. : Машиностроение, 2011. - 373 c. : ил., табл. (50 экз.)

9. Кудинов А.А. Строительная теплофизика: учеб.пособ. М.: ИНФРА-М, 2013. 295 с. (Высшее образование).

10. Методы интенсификации и моделирования тепломассообменных процессов [Текст] : учеб.-справ. пособие / А. Г. Лаптев, Н. А. Николаев, М. М. Башаров. - М. : Теплотехник, 2011. - 286 с. : граф., табл. - Библиогр.: с. 255-282. (5 экз.)

11. Кудинов А.А. Теплообмен и массообмен. Самара: Самар.гос.техн.ун-т, 2010. 373 с.

12. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. М.: Энергоиздат, 1981. (212 экз.)

13. Вычислительный практикум по курсам «Теплопередача» и «Основы тепло- и массообмена». Учебное пособие. А.В.Темников. Куйбышев, КПтИ, 1978. 70 с.

14. А.В.Темников. Современные методы математического моделирования и решения задач теплопроводности: Учеб.пособие. – Куйбышев: КПтИ, 1984, 90 с.

15. А.В.Темников, В.А.Бушев, В.Ф.Пеньков. Вычислительный практикум по курсу тепло- и массообмена: Учеб.пособие. – Куйбышев:КПтИ, 1988. 47 с.

 

 

Учебное издание

Габдушев Руслан Жамангараевич

Применение ЭВМ в тепловых расчетах

 

Печатается в авторской редакции

 

Подписано в печать ________________.

Формат 60 x 84 1/16. Бумага офсетная.

Печать офсетная.

Усл. п. л.. Уч..-изд. л.

Тираж 100 экз. Рег. №

 

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Самарский государственный технический университет»

443100, г. Самара, ул. Молодогвардейская, 244. Главный корпус

 

Отпечатано в типографии

Самарского государственного технического университета

443100, г. Самара, ул. Молодогвардейская, 244. Корпус №8

---

Дата добавления: 2018-02-28; просмотров: 568; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!