Свойства операций над матрицами. Образовательное учреждение высшего образования
Образовательное учреждение высшего образования
«Южно-Уральский институт управления и экономики»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
по выполнению домашней контрольной работы №2
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
Для студентов заочной формы обучения
По направлению:
13.03.02 «Электроэнергетика и электротехника»
Челябинск
2016
Номер варианта соответствует начальной букве фамилии студента.
| Начальная буква фамилии | Вариант задания |
| А, Е, Л | Первый |
| Р, Х, Э | Второй |
| Б, Ж, М | Третий |
| С, Ц, Ю | Четвертый |
| В, З, Н | Пятый |
| Т, Ч | Шестой |
| Г, И, О | Седьмой |
| У, Ш | Восьмой |
| Д, К, П | Девятый |
| Ф, Щ, Я | Десятый |
Задание №1. Выполнить операции над матрицами.
| 1 |
 * * 
|
| 2 |

|
| 3 |
5 
|
| 4 |
2 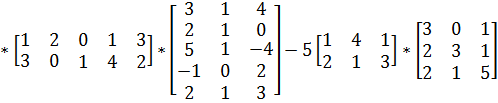
|
| 5 |
6 
|
| 6 |
3 
|
| 7 |
4  * * 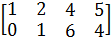
|
| 8 |
7  -5 -5 
|
| 9 |
6 
|
| 10 |
7 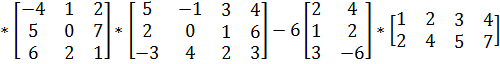
|
Задание №2. Вычислить пределы
|
|
|
|
|
|
|
|
|
|
Задание №3. Вычислить производную сложной функции.
| 1 | Y=(3x-4 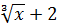 )4 )4
| Y= 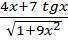
| Y=cos 3x* 
| Y=ln arctg2x |
| 2 | Y=(  -2 -2  )2 )2
| Y= 
| Y= 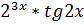
| Y= 
|
| 3 | Y=(  )4 )4
| Y= 
| Y= 
| Y= 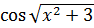
|
| 4 | Y= 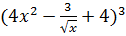
| Y= 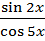
| Y= 
| Y= 
|
| 5 | Y= 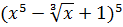
| Y= 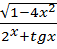
| Y= 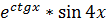
| Y= 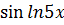
|
| 6 | Y= 
| Y= 
| Y= 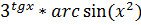
| Y=ln 
|
| 7 | Y= 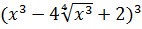
| Y= 
| Y= 
| Y= 
|
| 8 | Y= 
| Y= 
| Y= 
| Y=ln 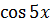
|
| 9 | Y= 
| Y= 
| Y= 
| Y=arc 
|
| 10 | Y= 
| Y= 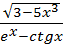
| Y= 
| Y=ln 
|
Задание №4.
|
|
|
А) Найти неопределенный интеграл заменой переменной
| 1 |

| 6 |

|
| 2 |

| 7 |
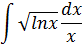
|
| 3 |

| 8 |

|
| 4 |

| 9 |

|
| 5 |
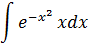
| 10 |
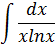
|
Б) Найти неопределенные интегралы, применяя метод интегрирования по частям.
| 1 | 
| 6 | 
|
| 2 | 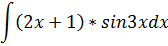
| 7 | 
|
| 3 | 
| 8 | 
|
| 4 | 
| 9 | 
|
| 5 | 
| 10 | 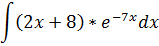
|
Задание № 5. Вычислить площадь фигуры, ограниченной линиями (площадь области D).
1. 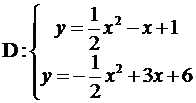
| 2. 
|
3. 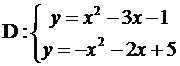
| 4. 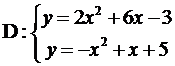
|
5. 
| 6. 
|
7. 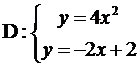
| 8. 
|
9. 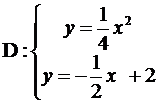
| 10. 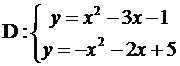
|
Методические материалы:
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Матрицы (и соответственно математический раздел - матричная алгебра)имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин "матрица" появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.
|
|
|
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.
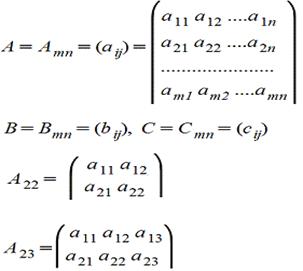
Элементы матрицы aij,у которых i=j, называются диагональными и образуют главную диагональ.
Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,..., ann .
Равенство матриц.
A=B, если порядки матриц A и B одинаковы и aij=bij(i=1,2,...,m; j=1,2,...,n)
Действия над матрицами.
1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция
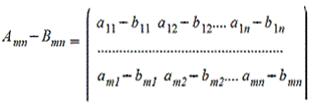
3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сijматрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

5. Возведение в степень
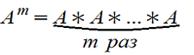
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц
|
|
|
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'

Строки и столбцы поменялись местами
Пример

Свойства операций над матрицами
A+B=B+A
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
Видыматриц
1. Прямоугольные: m и n - произвольные положительные целые числа
2. Квадратные: m=n
3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором
4. Матрица столбец: n=1. Например
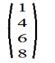
5. Диагональная матрица: m=n и aij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: aij=0, i=1,2,...,m
j=1,2,...,n
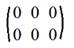
8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
Пример.

“ Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей”
Типы неопределенностей и методы их раскрытия
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей.
|
|
|
I. Неопределенность вида 
Пример 1. Вычислить предел 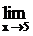

Решение: При подстановке вместо переменной х числа 5 видим, что получается неопределенность вида  . Для ее раскрытия нужно разложить знаменатель на множители: х2-25 = (х-5)*(х+5), получили общий множитель (х-5),на который можно сократить дробь. Заданный предел примет вид:
. Для ее раскрытия нужно разложить знаменатель на множители: х2-25 = (х-5)*(х+5), получили общий множитель (х-5),на который можно сократить дробь. Заданный предел примет вид: 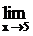
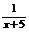 .Подставив х=5,получим результат:
.Подставив х=5,получим результат: 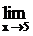
 =
= 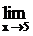
 =
= 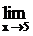
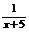 =
= 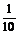
Пример 2. Вычислить предел 
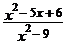
Решение: При подстановке вместо переменной х числа 3 видим, что получается неопределенность вида  . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х-3. В результате получим новый предел, знаменатель которого при подстановке вместо переменной х числа 3 не равен нулю. Этот предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х-3. В результате получим новый предел, знаменатель которого при подстановке вместо переменной х числа 3 не равен нулю. Этот предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.

Пример 3. Вычислить предел 

Решение: При подстановке вместо переменной х числа 0 видим, что получается неопределенность вида  . Для ее раскрытия воспользуемся первым замечательным пределом
. Для ее раскрытия воспользуемся первым замечательным пределом 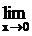
 и его следствием
и его следствием 
 . После чего предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.
. После чего предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.


II. Неопределенность вида 
Пример 4. Вычислить предел 
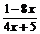
Решение: При подстановке вместо переменной х бесконечности ( 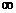 ) видим, что получается неопределенность вида
) видим, что получается неопределенность вида 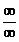 . Для ее раскрытия нужно числитель и знаменатель разделить на наивысшую степень, в данном случае на х. Получим:
. Для ее раскрытия нужно числитель и знаменатель разделить на наивысшую степень, в данном случае на х. Получим:

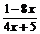 =
= 
 =
= 
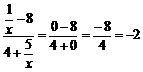 , т.к. величины
, т.к. величины 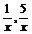 являются бесконечно малыми и их пределы равны 0.
являются бесконечно малыми и их пределы равны 0.
“Вычисление производных сложных функций”
Таблица производных основных элементарных функций:
1.  2.
2. 3.
3.  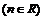 4.
4.  5.
5.  6.
6.  7.
7.  8.
8.  9.
9.  10.
10.  11.
11. 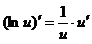
| 12. 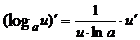 13.
13.  14.
14.  15.
15.  16.
16.  17.
17.  18.
18.  19.
19.  20.
20. 
|
“Интегрирование заменой переменной и по частям”
Таблица интегралов
1.  2.
2. 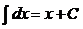 3.
3. 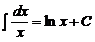 4.
4.  5.
5. 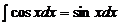 6.
6. 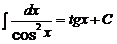
| 7.  8.
8. 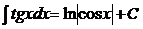 9.
9.  10.
10.  11.
11.  12.
12. 
| 13. 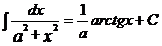 14.
14.  15.
15.  16.
16. 
|
Методы интегрирования
1. Непосредственное интегрирование
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Пример 1: Вычислите 
Решение: Для вычисления интеграла сначала воспользуемся 2 и 3 свойствами неопределенного интеграла, а затем применим 1 и 4 табличные интегралы:


Пример 2: Вычислите 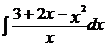
Решение: Для вычисления интеграла сначала каждый член числителя почленно разделим на знаменатель, затем воспользуемся 2 и 3 свойствами неопределенного интеграла и применим 1 и 3 табличные интегралы

2. Метод замены переменной (метод подстановки)
Он является одним из наиболее эффективных и распространенных приемов интегрирования, позволяющих вомногих случаях упростить вычисление интеграла. Суть этого метода состоит в том, что путем введения новой переменной интегрирования заданный интеграл сводится к новому интегралу, который легко вычисляется непосредственным интегрированием.
Пример 3: Вычислите 
Решение: Введем новую переменную t = 3x-4, тогда  , откуда
, откуда 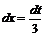 . Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо
. Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо  подставим
подставим  ).
).

Далее нужно вернуться к первоначальной переменной. Для этого сделаем обратную замену (вместо t подставим выражение 3х-4), получим окончательный ответ.
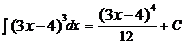
3. Метод интегрирования по частям
Рассмотрим функции  и
и  , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
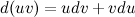
Проинтегрировав левую и правую части последнего равенства, получим:
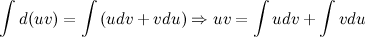
Полученное равенство перепишем в виде:
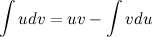
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл  можно свести к нахождению интеграла
можно свести к нахождению интеграла  , который может быть более простым.
, который может быть более простым.
Задание. Найти интеграл 
Решение. В исходном интеграле выделим функции  и
и  , затем выполним интегрирование по частям.
, затем выполним интегрирование по частям.

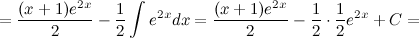
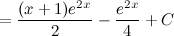
Ответ. 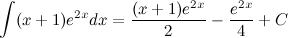
Задание. Найти интеграл 
Решение. В исходном интеграле выделим функции  и
и  , затем выполним интегрирование по частям. Для решения данного интеграла эту операцию надо повторить 2 раза.
, затем выполним интегрирование по частям. Для решения данного интеграла эту операцию надо повторить 2 раза.
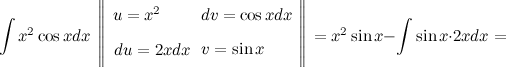

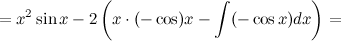


Ответ. 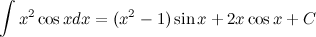
Задание. Найти интеграл 
Решение. В исходном интеграле выделим функции  и
и  , затем выполним интегрирование по частям.
, затем выполним интегрирование по частям.


Ответ. 
Задание. Найти интеграл 
Решение. В исходном интеграле выделим функции  и
и  , затем выполним интегрирование по частям. Для решения данного интеграла эту операцию надо повторить 2 раза.
, затем выполним интегрирование по частям. Для решения данного интеграла эту операцию надо повторить 2 раза.

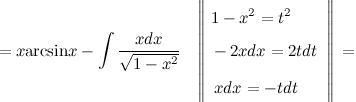

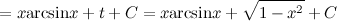
Ответ. 
“Вычисление площадей фигур с помощью определенных интегралов”
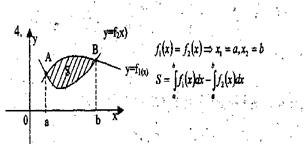
Площадь криволинейной трапеции, ограниченной непрерывной кривой у=f(х), двумя прямыми х=а и х=b и осью абсцисс, вычисляется с помощью определенного интеграла по формулам:
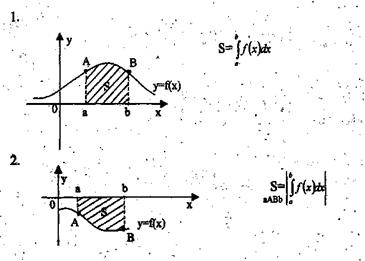

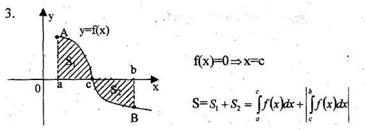
| 

|
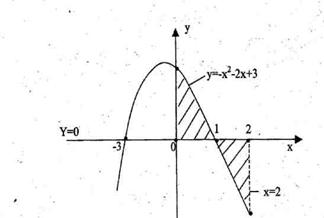
Пример: Вычислите площадь фигуры, ограниченной линиями  ,осями координат и прямой х=2.
,осями координат и прямой х=2.
Решение: Построим данные линии
|
|
Найдем точки пересечения графика функции с осью Ох:  ,
, 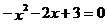 ,
, 



Дата добавления: 2018-02-28; просмотров: 461; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 ;
; 
 ;
; 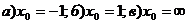
 ;
; 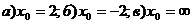
 ;
; 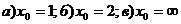
 ;
;  ;
;  ;
; 
 ;
; 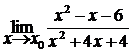 ;
;  ;
;