Оценка точности систем при случайных воздействиях

 

 

Реальные АС работают в условиях действия на них случайных возмущений. Это обусловлено нестабильностью внешних условий (температура, влажность, давление, ветер и т.п.), флуктуациями питающих напряжений.

 

Кроме того, в следящих системах задающее воздействие в общем случае описывается случайным процессом. И это обусловлено не только случайным характером, например, изменения положения объектом сопровождения, но и поступлением помехи на вход АС вместе с носителем полезной информации – радиосигналом.

 

Так, в системах автосопровождения цели на вход поступает несколько случайных возмущений, обусловленных следующими причинами:

 

− федингом;

 

− угловым шумом (блужданием центра отражения);

 

− шумами первых каскадов приемника.

51

 

Фединг –это флуктуация амплитуды принимаемого радиосигнала,обусловленные характером отражения электромагнитных волн от сложных поверхностей и изменениями плотности атмосферы.

 

Блуждание центра отражения –это флуктуации принимаемого сигнала,обусловленные сложением фаз сигналов, отраженных от элементарных площадок поверхности цели.

 

Шум приемника –обусловлен такими явлениями как тепловой шум,дробовой шум (для электронных ламп), шум мерцания (фликкер-эффект), генераторно-рекомбинационный шум (в полупроводниках).

 

В результате перечисленных причин как рассогласование в системе, ошибка слежения, так и управляемая величина являются случайными процессами.

 

В большинстве случае закон распределения случайных значений ошибки

 

и выходной величины можно считать нормальным (гауссовским), который полностью описывается его математическим ожиданием и корреляционной функцией. Если процессы являются также и стационарными, то для их описаний вместо корреляционной функции используется спектральная

плотность S(ω), которые связаны между собой преобразованием Фурье. Тогда,

 

для сигнала ошибки можно записать

R _ε ( τ) = ₂¹_π ^∞_∫S_ε ( ω ) _e^jωτ dω _.

−∞

 

Средней квадратической ошибкой системы называют величину

 

σ =  m²_ε + σ²_{ε ;}

где m_ε – математическое ожидание сигнала ошибки;

 

D_ε =σ_ε² – дисперсия сигнала ошибки.

 

МО m_ε рассчитывают по теореме о конечном значении

m _ε = _limS Φ_ε ( S) m_x ( S) _.

 

S→0

52

 

Точность системы относительно случайных составляющих сигнала и помехи оценивается дисперсией ошибки

 

σ ²_ε = M[ε ² ( t ) ]= R_ε ( τ) _{τ=0 .}

 

Проведенные исследования показывают, что дисперсия искомой ошибки может быть найдена по формуле

 

σ ²_ε = σ ²_εx + σ²_{εf .}

 

 

Из этой зависимости следует, что суммарная ошибка состоит из двух составляющих, одна из которых m_ε²+σ_ε², определяющая точность воспроизведения сигнала, зависит от ПФ ошибки и статистических характеристик сигнала Х, а вторая, обусловленная действием помехи σ_εf² – от ПФ замкнутой системы и характеристик помехи.

 

Аналогично находятся частотные и статистические характеристики случайной выходной величины Y(t). Например, если задающее воздействие является случайной функцией с нулевым МО и спектральной плотностью

 

S_x(ω), то спектральная плотность и дисперсия выходной величины определяются выражениями

 

S _Y ( ω ) = Φ( j ω ) ² S _x ( ω ); σ_Y² = ₂¹_π ^∞_∫S_Y ( ω ) d ω _.

−∞

 

 

Пример

 

Определить порядок астатизма системы по задающему ν_x и

 

возмущающему ν_f воздействиям, а также установившиеся ошибки системы от

53

 

задающего и возмущающего воздействий, если x(t)=x₀⋅1(t), f(t)=f₀⋅1(t), а

 

структурная схема системы имеет вид (рис.20)

 

 

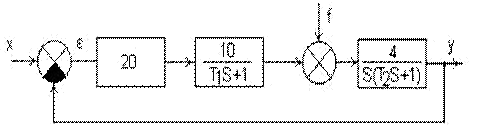
Рис. 21. Структурная схема АС

 

Решение. Порядок астатизма по задающему воздействию определяется числом интегрирующих звеньев во всем контуре управления. Поэтому ν_x=1.

 

Порядок астатизма по возмущающему воздействию равен числу ИЗ, находящихся между точкой применения воздействия и точкой наблюдения сигнала ошибки. В данном случае ν_f=0.

 

Передаточная функция для ошибки замкнутой системы по задающего

 

Фε(S) и возмущающего Фεf(S) воздействий имеют вид

Φε ( S) =

1

=

( T1S + 1)( T2 S + 2)S

;

1 + W ( S)

( T

1

S + 1)( T S + 1) S + 800

2

Φεf (S) =

Wf (S)

=

4 ( T1S +1)( T2 S +1)S

=

1 + W (S)

( T S

+ 1)S

(T S + 1)( T S

+ 1)S + 800

2

[

1

2

]

=

4 ( T1S +1)

.

( T S + 1)( T S + 1)S + 800

1

2

 

По теореме Лапласа о конечном значении оригинала

 

εx уст = limS ⋅	x 0	⋅	( T1S + 1)( T2 S +1)S	= 0 ;
	S		( T1S + 1)( T2 S + 1)S + 800
S→0

54

 

εf уст = limS ⋅

f 0

⋅

4 ( TS +1)

= −

f 0 ⋅4

= −

f 0 ⋅k f

= −0.005f0 ,

S

( TS

+ 1)( TS + 1)S +800

k

S→0

800

с учетом того, что x (S) =

x0

=

f0

; f (S)

.

S

S

 

---

Дата добавления: 2018-02-28; просмотров: 461; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!