Табличный способ задания функции
При табличном способе задания функции рядом с числовым значением аргумента записывается соответствующее значение функции. Широко известных таблицы квадратов и кубов чисел, квадратных корней, то есть таблицы функций 
, 
, 
.
Недостатком табличного способа задания функции является то, что в таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности изменения функции при этом могут быть искажены или утрачены.
Сложная функция
Если функция y зависит от переменной u, то есть y = f(u), а u, в свою очередь, является какой-либо функцией от независимой переменной x, то есть u = g(x), то переменная y называется функцией от функции или сложной функцией от x.
Это записывается в виде
y = f(u), u = g(x)
или
y = f[g(x)].
Таким образом, сложной называется функция, аргументом которой является не независимая переменная, а некоторая функция от неё.
Область определения сложной функции - это множество тех значений x из X, для которых соответствующие значения u принадлежат области определения U функции y = f(u). Ни для каких других значений x сложная функция не имеет смысла.
Из определения следует, что сложная функция y = f[g(x)] может быть представлена в виде цепочки простых функций y = f(u), u = g(x). Переменную u принято называть промежуточным аргументом в отличие от независимой переменной x. Цепочка, составляющая сложную функцию, может состоять не только из двух, но и из большего числа звеньев.
|
|
|
Например, функция 
состоит из трёх звеньев: 
, 
, 
.
Пример 5.Представить сложную функцию 
в виде звеньев - простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих звеньев:
Пример 6.Представить сложную функцию 
в виде звеньев - простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих звеньев:
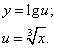
Обратная функция
Если функция y задана уравнением вида f(x, y) =0, не разрешённым относительно y, то она называется неявной функцией аргумента x (Что такое разрешить уравнение относительно одной из переменных - в примере 8).
Пусть задана некоторая функция y = f(x), т. е. некоторое соответствие между множествами D(f) (область определения) и E(f) (множество значений). Если обратное соответствие есть функция, т. е. каждому значению y∈E(f) соответствует одно единственное значение x∈E(f), то её называют обратной функцией по отношению к функции f(x).
В этом случае уравнение y = f(x) определяет x как неявную функцию от y. Если это уравнение разрешимо относительно x, то получим явное выражение обратной функции: x = g(y).
Пример 7.Будет ли функцией соответствие, обратное функции 
? А соответствие, обратное функции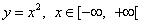 
?
Решение. Соответствие, обратное функции, заданной в первом условии, также является функцией:
|
|
|
.
Соответствие, обратное функции, заданной во втором условии, не является функцией, так как 
, то есть значениям икса, кроме нуля, соответствуют два значения игрека.
Пример 8.Найти функцию, обратную функции 
.
Решение. Множество значений данной функции 
. Разрешив уравнение, которым задана функция, относительно x, получаем 
. Заменив в этом уравнении x на y, получим функцию, обратную данной:
, где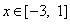 
, 
.
Дата добавления: 2018-02-28; просмотров: 1231; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!