Несобственные интегралы с бесконечным нижним пределом
Аналогично определяется несобственный интеграл от непрерывной функции с бесконечным нижним пределом интегрирования, обозначаемый символом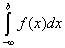 
, а именно
.
Если этот предел существует (и, значит, конечен, то есть, равен некоторому числу, а не бесконечности), то данный несобственный интеграл называется сходящимся.
Пример 6. Вычислить несобственный интеграл 
с бесконечным нижним пределом(если он сходится).
Решение. Находим предел данного интеграла:
Итак, данный несобственный интеграл сходится, а его значение равно -1/2.
Несобственные интегралы с двумя бесконечными пределами
Несобственный интеграл с двумя бесконечными пределами интегрирования, обозначаемый символом 
, нужно предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой - с конечным нижним пределом интегрирования, т.е.
.
По определению,
,
причём этот несобственный интеграл считается сходящимся, если оба предела существуют, когда a и b независимо друг от друга неограниченно возрастают по абсолютной величине.
Пример 7. Вычислить несобственный интеграл 
с двумя бесконечными пределами (если он сходится).
Решение. На основании определения несобственного интеграла с двумя бесконечными пределами представляем данный интеграл как сумму двух несобственных интегралов:
.
Преобразуем подынтегральное выражение к форме 
, с помощью выделения полного квадрата:
|
|
|
По формуле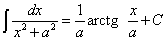 
находим:
(Эта формула, которой мы воспользовались, а также другие формулы, пригодные для интегрирования дробей, приведены в уроке Интегрирование некоторых рациональных дробей и иррациональностей).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
.
Несобственные интегралы второго рода - от неограниченных функций и их сходимость
Пусть функция f(x) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b, в то время как во всех остальных точках отрезка она непрерывна.
Определение.Несобственным интегралом функции f(x) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c, если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена, т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.
|
|
|
Используя формулу Ньютона-Лейбница, получаем
.
Это также обобщённая формула Ньютона-Лейбница. Именно она применяется в решении задач на вычисление несобственных интегралов от неограниченных функций.
Пример 8. Вычислить несобственный интеграл 
(если он сходится).
Решение. Подынтегральная функция при 
неограниченно возрастает, а в точке x = 0 функция не определена, то есть, не существует. Используя обобщённую формулу Ньютона-Лейбница, получаем
(так как при x = 0 первообразная непрерывна). Итак, данный несобственный интеграл сходится и равен -3/2.
Пример 9. Вычислить несобственный интеграл 
(если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке полуотрезка[0, 1]. В точке x = 1 функция обращается в бесконечность. Если взять 
, то на [0, c] подынтегральная функция непрерывна и, следовательно, существует интеграл.
.
Найдём предел этого интеграла:
Таким образом, несобственный интеграл сходится и его значение мы нашли.
Пример 10. Исследовать на сходимость несобственный интеграл 
(верхний предел интегрирования больше нижнего).
Решение. Подынтегральная функция обращается в бесконечность при x = b, в остальных точках она непрерывна. Предположим сначала, что 
, тогда для 
:
|
|
|
В полученном выражении перейдём к пределу при 
:
Нетрудно видеть, что предел в правой части существует и равен нулю, когда 
, то есть 
, и не существует, когда 
, то есть 
.
В первом случае, то есть при
.
Если 
, то
.
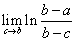не существует.
Таким образом, вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходитсяпри 
.
Дата добавления: 2018-02-28; просмотров: 740; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!