Интегрирование иррациональных функций: способы и примеры решений

В подынтегральном выражении - различные дробно-рациональные функции
Корень из квадратного трёхчлена и подстановки Эйлера
Интегралы от дифференциального бинома и подстановки Чебышева
Частный случай квадратичных иррациональностей

Рассмотрим интегралы от иррациональных функций, то есть функций, содержащих переменную (обычно икс) под корнем или, что то же самое - в дробной степени. Интегралы от таких функций с помощью подстановок приводятся к интегралам от рациональных функций и могут быть проинтегрированы окончательно.

В подынтегральном выражении - различные дробно-рациональные функции

Разберём интегралы, где в подынтегральном выражении переменная присутствует под корнем. В формально обобщённом виде речь идёт об интегралах вида

где λ, ... μ - рациональные числа (целые или дробные).

В примерах мы увидим, что переменная икс, присутствующая под корнем, присутствует там без степени. В примере 3 икс присутствует также в квадрате, но при этом - не по корнем. То есть корни отдельно, степени - отдельно.

В этом случае важное значение имеет наименьшее общее кратное чисел λ, ... μ (или общий знаменатель, если эти числа дробные). Обозначим это наименьшее общее кратное (общий знаменатель) через n. Рассматриваемые интегралы от иррациональных функций можно найти, используя следующую подстановку:

Тогда каждая дробная степень "икса" выразится через целую степень "тэ" и подынтегральная функция преобразуется в рациональную функцию от "тэ".

Пример 1. Найти интеграл от иррациональной функции .

Решение. Преобразуем все корни икса в степени. Выписываем степени при иксе в подынтегральном выражении - все, которые там находим:

Находим наименьшее общее кратное знаменателей этих чисел: 4.

Поэтому используем следующую подстановку:

Подставляем и преобразуем:

Начинаем интегрировать:

Возвращаясь к переменной икс, окончательно находим:

Пример 2. Найти интеграл от иррациональной функции .

Решение. Используем следующую подстановку:

Подставляем и преобразуем:

Интегрируем и получаем:

Возвращаясь к переменной икс, окончательно находим:

Понятие определённого интеграла и формула Ньютона-Лейбница

Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) - F(a)).

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.

Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,

(38)

Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:

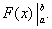
Поэтому формулу Ньютона-Лейбница будем записывать и так:

(39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому

Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. ПостояннаяСиз последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего пределаb, далее - значение нижнего пределаaи вычисляется разностьF(b) - F(a). Полученное число и будет определённым интегралом..

При a = b по определению принимается

Для того чтобы потренироваться в нахождении определённых интегралов, потребуется таблица основных неопределённых интегралов и пособие "Действия со степенями и корнями".

Пример 1.Вычислить определённый интеграл