Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму
Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида
 (1)
(1)
Воспользовавшись известными тригонометрическими формулами
 (2)
(2)
 (3)
(3)
 (4)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам
 (5)
(5)
и
 (6)
(6)
Пример 1.Найти интеграл от тригонометрической функции
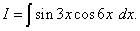
Решение. По формуле (2) при

имеем

Поэтому

Применяя далее формулу (5), получим
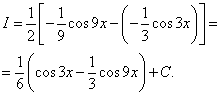
Пример 2.Найти интеграл от тригонометрической функции

Решение. По формуле (3) при  получаем следующее преобразование подынтегрального выражения:
получаем следующее преобразование подынтегрального выражения:

Поэтому

Применяя далее формулу (6), получим
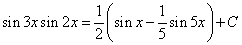
Пример 3.Найти интеграл от тригонометрической функции

Решение. По формуле (4) при  получаем следующее преобразование подынтегрального выражения:
получаем следующее преобразование подынтегрального выражения:

Применяя формулу (6), получим
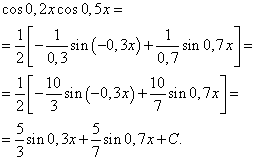
Интеграл произведения степеней синуса и косинуса одного и того же аргумента
Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.
 (7)
(7)
В частных случаях один из показателей (m или n) может равняться нулю.
При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен - sin x dx).
|
|
|
Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.
Пусть имеет место первый случай, а именно показатель n = 2k + 1 - нечётный. Тогда, учитывая, что

получим

Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t. Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx, выражая остальную часть подынтегральной функции через cosx и полагая t = cos x. Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса, когда хотя бы один из показателей - нечётный. Всё дело в том, что частное степеней синуса и косинуса - это частный случай их произведения: когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень - отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени - только чётные. О них - следующем абзаце.
Если же оба показателя m и n – чётные, то, используя тригонометрические формулы
|
|
|

понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей - отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится. Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.
Пример 4.Найти интеграл от тригонометрической функции

Решение. Показатель степени косинуса – нечётный. Поэтому представим

в виде

и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим

Возвращаясь к старой переменной, окончательно найдём

Пример 5.Найти интеграл от тригонометрической функции
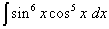 .
.
Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим

в виде

и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим

Раскроем скобки
 и получим
и получим
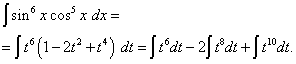
Возвращаясь к старой переменной, получаем решение

Пример 6.Найти интеграл от тригонометрической функции

Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:
|
|
|

Тогда получим

Во втором интеграле произведём замену переменной, полагая t = sin2x. Тогда (1/2)dt = cos2x dx. Следовательно,

а

Окончательно получаем

Дата добавления: 2018-02-28; просмотров: 626; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
