Применяем интегрирование по частям вместе
Суть метода замены переменной
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной. Он основан на следующей теореме.
Теорема.Пусть функция  определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
 (1)
(1)
Формула (1) называется формулой замены переменной в неопределённом интеграле.
Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.
Применяем замену переменной вместе
Надо полагать, вы уже держите перед собой домашние задания и готовы применять к ним приёмы по аналогии с теми, которые мы ниже рассмотрим. При этом не обойтись без преобразований выражений. Для этого потребуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Пример 1. Найти неопределённый интеграл методом замены переменной:

Решение. Положим x – 1 = t ; тогда x = t + 1. Отсюда dx = dt. По формуле (1)
|
|
|

Возвращаясь к переменной x, окончательно получаем

Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.
Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.
Пример 2. Найти неопределённый интеграл методом замены переменной:
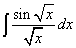 .
.
Решение. Положим  .Отсюда
.Отсюда
 .
.
По формуле (1)
 .
.
Возвращаясь к переменной x, окончательно получаем

Если трудно уследить, куда в процессе решения примера 2 делись  и
и  , это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.
, это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.
Пример 3. Найти неопределённый интеграл методом замены переменной:
 .
.
Решение. Положим  , откуда
, откуда 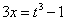 и
и  .
.
Тогда  , в свою очередь
, в свою очередь 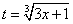 .
.
Заменяем переменную и получаем:
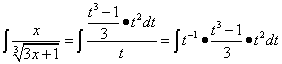 ,
,
где степени при t складываются. Продолжаем преобразования и получаем:

Приводим дроби к общему знаменателю и возвращаемся к переменной x. Решаем и получаем ответ:

Уть метода интегрирования по частям
Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:
|
|
|

Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u, а остальная часть относится ко второму множителю и обозначается через dv. Затем дифференцированием находится du и интегрированием - функция v. При этом за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv - такую часть подынтегрального выражения, которая легко интегрируется.
Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит:
1)  - логарифмические функции, а также обратные тригонометрические функции (с приставкой "arc"), тогда на основании продолжительного опыта интегрирования по частям эти функции обозначаются через u;
- логарифмические функции, а также обратные тригонометрические функции (с приставкой "arc"), тогда на основании продолжительного опыта интегрирования по частям эти функции обозначаются через u;
2)  ,
,  ,
,  - синус, косинус и экспоненту, умноженные на P(x) - произвольный многочлен от икса, тогда эти функции обозначают через dv, а многочлен - через u;
- синус, косинус и экспоненту, умноженные на P(x) - произвольный многочлен от икса, тогда эти функции обозначают через dv, а многочлен - через u;
3)  ,
,  ,
,  ,
,  , в этом случае интегрирование по частям применяется дважды.
, в этом случае интегрирование по частям применяется дважды.
Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.
|
|
|
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:

Так как

то её можно записать в виде
 ,
,
который и был приведён в самом начале урока.
При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С, равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.
Применяем интегрирование по частям вместе
Пример 1. Найти неопределённый интеграл методом интегрирования по частям:
 .
.
Решение. В подынтегральном выражении - логарифм, который, как мы уже знаем, разумно обозначить через u. Полагаем, что  ,
,  .
.
Тогда  ,
, 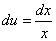 .
.
Находим:

И снова логарифм...
Пример 2.Найти неопределённый интеграл:
 .
.
Решение. Пусть  ,
, 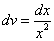 .
.
Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим
 ,
,
 .
.
Применяя формулу интегрирования по частям, получаем:
|
|
|

Второй интеграл вновь находим по частям.


Находим изначальный интеграл:
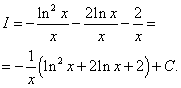
Пример 3.Найти неопределённый интеграл методом интегрирования по частям:
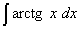 .
.
Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть 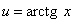 ,
, 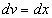 .
.
Тогда  ,
,
 .
.
Применяя формулу интегрирования по частям, получаем:

Второй интеграл находим методом замены переменной.


Возвращаясь к переменной x, получаем
 .
.
Находим изначальный интеграл:
 .
.
Пример 4. Найти неопределённый интеграл методом интегрирования по частям:
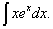
Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что

находим

Пример 5. Найти неопределённый интеграл методом интегрирования по частям:
 .
.
Решение. Пусть  ,
,  . Тогда
. Тогда  ,
,  .
.
Используя формулу интегрирования по частям (1), находим:

Пример 6.Найти неопределённый интеграл методом интегрирования по частям:
 .
.
Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть  ,
,  .
.
Тогда  ,
,  .
.
По формуле интегрирования по частям находим:

Дата добавления: 2018-02-28; просмотров: 505; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
