Основные теоремы и утверждения
Основные понятия теории вероятностей. События. Алгебра событий. Классическое определение вероятности события
Основные определения
Испытание – неопределяемое понятие, понимается как наблюдение того или иного явления.
Событие – возможный исход того или иного испытания.
Классификация событий
· Достоверное событие– событие, которое обязательно происходит в результате испытания.
· Невозможное событие – событие, которое вообще не может произойти в результате испытания.
· Случайное событие – событие, которое в результате испытания может произойти, а может и не произойти.
Численная мера степени объективной возможности наступления события называется вероятностью события, и обозначается: P(A).
Определение
Пусть исходы некоторого испытания образуют полную группу событий и равновозможные. Такие события (исходы) называются элементарными исходами (другими словами – это общее число исходов испытания).
Определение
Случай называется благоприятствующим событию A, если его появление влечет за собой появление события A.
Основные утверждения и теоремы
Согласно классическому определению, вероятность события A есть отношение числа случаев благоприятствующих событию к общему числу исходов испытания: 
, где m – число случаев, благоприятствующее событию A; n – общее число исходов испытания.
Для отыскания общего числа исходов испытания и числа исходов, благоприятствующих некоторому событию можно использовать основные правила и формулы комбинаторики.
|
|
|
Правило суммы
Если элемент а1 может быть выбран n1 способами, а2 – n2 способами, отличными от первого, …ак – nк- способами, отличными от (к-1), то выбор одного из элементов а1, или а2,…или ак может быть осуществлен n1+n2+…+nkспособами.
Правило произведения
Если элемент а1 может быть выбран n1 способами, а2 – n2 способами, …, после (к-1) выбора, элемент ак может быть выбран nк способами, то выбор всех элементов а1, а2, …, ак в указанном порядке может быть осуществлен n1n2…nk способами.
Элементы комбинаторики: размещение из n элементов по m, размещение из n элементов по m с повторением, сочетания из n элементов по m, перестановки из n элементов.
, 
Основные алгоритмы
Использование классического определения при нахождении вероятности события
1) Найти общее число исходов испытания.
2) Сформулировать событие.
3) Найти число исходов испытания, благоприятствующих событию.
4) Провести расчет вероятности события по классическому определению вероятности.
Пример
В арсенале знаний студентов по теме 11 формул из 15. Какова вероятность того, что в процессе решения задачи будет использоваться формула, которую он знает.
|
|
|
Решение
Испытание: использование формулы в процессе решения задачи
, т.к. общее число формул по теме – 15.
А= {в процессе решения задачи студент использует формулу, которую он знает}
, т.к. число формул, которые он знает – 11.
Тогда по классическому определению вероятности события 
.Ответ: 
.
Теоремы сложения и умножения вероятностей
Основные определения
Определение
Два события называются несовместными, если наступление одного из них исключает наступление другого, в ином случае они называются совместными.
Определение
Несколько событий называются единственно возможными, если в результате испытания обязательно произойдет хотя бы одно из них.
Определение
Несколько событий образуют полную группу, если они являются единственно возможными и несовместными исходами испытания.
Частным случаем событий, образующих полную группу, являются противоположные события.
Определение
Два несовместных события, из которых одно должно обязательно произойти, называются противоположными. Событие противоположное событию A обозначается: 
.
Действия над событиями
Определение:
|
|
|
Суммой нескольких событий называется событие, состоящее в том, что произойдет хотя бы одно из данных событий.
Определение
Произведением нескольких событий называется событие, состоящее в совместном появлении каждого из данных событий.
Определение
События называются независимыми, если происхождение одного не изменяет вероятности происхождения другого (других), иначе они зависимые.
Замечание
Попарная независимость нескольких событий еще не означает независимость их совокупности.
Основные теоремы и утверждения
Теорема сложения вероятностей несовместных событий:
Вероятность появления одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий
Следствие
Сумма вероятностей событий, образующих полную группу, равна единице
, где А1, А2,…,Аn образуют полную группу событий.
Следствие
Сумма вероятностей противоположных событий равна единице
Теорема умножения вероятностей независимых событий:
Вероятность произведения двух или нескольких независимых событий равна произведению вероятностей этих событий
Теорема сложения вероятностей совместных событий:
Теорема умножения вероятностей зависимых событий:
|
|
|
, где 
- условная вероятность.
Основные алгоритмы
Использование теорем сложения и умножения при вычислении вероятности данного события.
1) Сформулировать данное событие, вероятность которого следует найти.
2) Сформулировать элементарные события.
3) Составить конструкцию данного события с помощью элементарных событий и действий над событиями.
4) Выбрать одну или несколько теорем сложения и умножения, в зависимости от вида элементарных событий и конструкции события.
5) Провести расчет вероятности данного события.
Пример
Студент знает 20 из 25 вопросов программы. Найдите вероятность того, что
1) студент знает предложенные ему экзаменатором 3 вопроса;
2) студент ответит хотя бы на один вопрос из 3-х.
Решение
1) А={событие, что студент ответит на все 3 вопроса}
Обозначим А1={событие, что студент ответил на первый вопрос}
А2={событие, что студент ответил на второй вопрос}
А3={событие, что студент ответил на третий вопрос}.
Тогда А= А1и А2 и А3, т.е. А= А1 А2 А3
Р(А)=Р(А1 А2 А3)=Р(А1)Р(А2/A1)P(A3/A1A2)= 
. Ответ: 
1.3.Формула полной вероятности, формула Байеса
Основные определения
Пусть событие А происходит с одним из событий H1, H2, …, Hn, образующих полную группу попарно несовместных событий. События H1, H2, …, Hn называются гипотезами.
Основные теоремы
Теорема (формула полной вероятности)
Если A может произойти только при появлении одной из гипотез H1, H2, …, Hn. Тогда вероятность появления события А равна сумме произведений вероятностей гипотез на условные вероятности события А при каждой гипотезе: 
.
Теорема (Формула Байеса)
Пусть H1, H2, …, Hn, - полная группа событий и А- произвольное событие, которое может произойти только с одной из гипотез Hi, 
. Тогда для каждого 
справедливо равенство 
.
Основные алгоритмы
Использование формулы полной вероятности при вычислении вероятности данного события или формулы Байеса для переоценки вероятности гипотез, известных до испытания.
1) Сформулировать совокупность гипотез, образующих полную группу событий, найти их вероятности.
2) Сформулировать событие, найти его вероятность или условную вероятность одной из гипотез.
3) Записать ответ.
Пример
Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит первому стрелку?
Решение
1) Обозначим события: 
-={первый стрелок попал в мишень, 2-ой не попал};
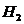={первый стрелок не попал в мишень, 2-ой попал};
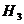={ оба стрелка попали в мишень};
={ оба стрелка не попали в мишень}.
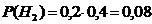
Отметим, что 
2) А={событие, что в мишени одна пробоина}.
1;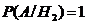 
; 
; 
.
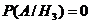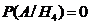По формуле Байеса имеем: 
. Ответ: 
1.4.Повторные независимые испытания
Основные определения
Пусть некоторый эксперимент повторяется n-раз, причем вероятность наступления события А не меняется в зависимости от исходов других событий. Такие серии повторений называют независимыми испытаниями.
Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:
1) вероятность наступления события А в каждом испытании одна и та же;
2) результатом каждого испытания является один из двух возможных исходов.
Определение
Число k0 наступления события А в n независимых испытаниях называетсянаивероятнейшим,если вероятность того, что событие наступит в этих испытаниях k0 раз, превышает (или по крайней мере, не меньше) вероятности остальных возможных исходов испытаний. Наивероятнейшее число k0 определяют из двойного неравенства:
np-q 
k0<np+p, причем, если
1) np-q –дробное, то существует одно наивероятнейшее число k0;
2) np-q –целое, то существует два наивероятнейших числа k0 и k0+1;
3) np – целое, то наивероятнейшее число k0=np.
Основные теоремы
Теорема (формула Бернулли)
Если вероятность р наступления события А в каждом испытании постоянна, то вероятность того, что событие А наступит m-раз в n независимых испытаниях, равна
Дата добавления: 2018-02-28; просмотров: 419; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!