Равносильные преобразования. Упрощение формул
Раздел 2. Логическая равносильность формул. Нормальные формы для формул алгебры высказываний
Отношение равносильности
С помощью таблиц истинности можно установить, при каких наборах значений истинности входящих переменных формула будет принимать истинное или ложное значение (а также высказывание, имеющее соответствующую логическую структуру), какие формулы будут тавтологиями или противоречиями, а также установить, являются ли две данные формулы равносильными.
В логике говорят, что два предложения равносильны, если они одновременно истинны, либо одновременно ложны. Слово «одновременно» в этой фразе неоднозначно. Так, для предложений «Завтра будет вторник» и «Вчера было воскресенье» это слово имеет буквальный смысл: в понедельник они оба истинны, а в остальные дни недели – оба ложны. Для уравнений «х = 2» и «2х = 4» «одновременно» означает «при одних и тех же значениях переменной». Прогнозы «Завтра будет дождь» и «Неверно, что завтра не будет дождя» одновременно подтвердятся (окажутся истинными) либо не подтвердятся (окажутся ложными). В сущности, это один и тот же прогноз, выраженный в двух разных формах, которые можно представить формулами Х и 
. Эти формулы одновременно принимают значение «истина» либо значение «ложь». Для проверки достаточно составить таблицу истинности:
| Х | 
|
|
| 1 | 0 | 1 |
| 0 | 1 | 0 |
Видим, что значения истинности в первом и последнем столбцах совпадают. Такие формулы, как и соответствующие им предложения, естественно считать равносильными.
|
|
|
Формулы F1 и F2 называются равносильными, если их эквиваленция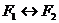 
– тавтология.
Равносильность двух формул записывается так: 
(читается: формула F1 равносильна формуле F2).
Проверить, равносильны ли формулы, можно тремя способами: 1) составить их эквиваленцию и с помощью таблицы истинности проверить, не является ли она тавтологией; 2) для каждой формулы составить таблицу истинности и сравнить итоговые результаты; если в итоговых столбцах при одинаковых наборах значений переменных значения истинности обеих формул будут равны, то формулы являются равносильными; 3) с помощью равносильных преобразований.
Пример 2.1: Выяснить, являются ли формулы равносильными: 1) 
, 
; 2)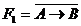 
, 
.
Решение.
1) Воспользуемся для определения равносильности первым способом, то есть выясним, является ли эквиваленция формул и тавтологией.
Составим эквиваленцию формул: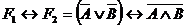 
. Полученная формула содержит две различные переменные (А и В) и 6 операций: 1) 
; 2) 
; 3) 
; 4) 
; 5) 
; 6) 
. Значит, в соответствующей таблице истинности будет 5 строк и 8 столбцов:
| А | В |
|
|
|
|
|
|
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
Из итогового столбца таблицы истинности видно, что составленная эквиваленция является тавтологией и, значит, .
|
|
|
2) Для того чтобы выяснить являются ли формулы 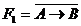и равносильными, используем второй способ, то есть составим для каждой из формул таблицу истинности и сравним итоговые столбцы. (Замечание. Для того чтобы эффективно использовать второй способ, необходимо, чтобы все составленные таблицы истинности начинались одинаково, то есть наборы значений переменных были одинаковы в соответствующих строках.)
В формуле 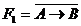две различные переменные и 2 операции, значит, в соответствующей таблице истинности 5 строк и 4 столбца:
| А | В | 
| 
|
| 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 |
В формуле две различные переменные и 3 операции, значит, в соответствующей таблице истинности 5 строк и 5 столбцов:
| А | В |
|
| 
|
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
Сравнивая итоговые столбцы составленных таблиц истинности (так как таблицы начинаются одинаково, мы можем не обращать внимание на наборы значений переменных), видим, что они не совпадают и, следовательно, формулы не равносильны ( 
).
|
|
|
Выражение 
не является формулой (так как символ «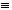 
» не относится к какой-либо логической операции). Оно выражает отношение между формулами (также как равенство между числами, параллельность между прямыми и т.п.).
Справедлива теорема о свойствах отношения равносильности:
Теорема 2.1. Отношение равносильности между формулами алгебры высказываний:
1) рефлексивно: 
;
2) симметрично: если , то 
;
3) транзитивно: если и 
, то 
.
Законы логики
Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них:
1. 
– закон тождества.
2. 
– закон исключенного третьего
3. 
– закон противоречия
4. 
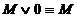– дизъюнкция с нулем
5. 
– конъюнкция с нулем
6. 
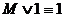– дизъюнкция с единицей
7. 
– конъюнкция с единицей
8. 
– закон двойного отрицания
9. 
– коммутативность конъюнкции
10. 
– коммутативность дизъюнкции
11. 
– ассоциативность конъюнкции
12. 
– ассоциативность дизъюнкции
13. 
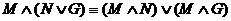– дистрибутивность конъюнкции
14. 
– дистрибутивность дизъюнкции
15. 
– законы идемпотентности
16. 
; 
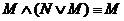– законы поглощения
17. 
; 
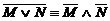– законы де Моргана
18. 
– закон, выражающий импликацию через дизъюнкцию
|
|
|
19. 
– закон контрапозиции
20. 
– законы, выражающие эквиваленцию через другие логические операции
Законы логики используются для упрощения сложных формул и для доказательства тождественной истинности или ложности формул.
Равносильные преобразования. Упрощение формул
Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными в соответствии с правилом подстановки. Таким способом из каждой равносильности можно получить сколько угодно новых равносильностей.
Пример 1:Если в законе де Моргана 
вместо Х подставить 
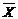, а вместо Y подставить 
, то получим новую равносильность 
. Справедливость полученной равносильности легко проверить с помощью таблицы истинности.
Если какую-нибудь формулу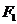 
, являющуюся частью формулы F, заменить формулой 
, равносильной формуле 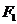, то полученная формула окажется равносильной формуле F.
Тогда для формулы из примера 2 можно провести следующие замены:
– закон двойного отрицания;
– закон де Моргана;
– закон двойного отрицания;
– закон ассоциативности;
– закон идемпотентности.
По свойству транзитивности отношения равносильности можем утверждать, что 
.
Замену одной формулы другой, ей равносильной, называют равносильным преобразованием формулы.
Под упрощением формулы, не содержащей знаков импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая не содержит отрицаний неэлементарных формул (в частности, двойных отрицаний) или содержит в совокупности меньшее число знаков конъюнкции и дизъюнкции, чем исходная.
Пример 2.2: Упростим формулу 
.
.
На первом шаге мы применили закон, преобразующий импликацию в дизъюнкцию. На втором шаге применили коммутативный закон. На третьем шаге применили закон идемпотентности. На четвертом – закон де Моргана. И на пятом – закон двойного отрицания.
Замечание 1. Если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией.
Таким образом, равносильные преобразования можно также применять для доказательства тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями привести к одной из формул, которые являются тавтологиями.
Замечание 2. Некоторые тавтологии и равносильности объединены в пары (закон противоречия и закон альтернативы, коммутативный, ассоциативный законы и т.д.). В этих соответствиях проявляется так называемый принцип двойственности.
Две формулы, не содержащие знаков импликации и эквиваленции, называются двойственными, если каждую из них можно получить из другой заменой знаков 
соответственно на 
.
Принцип двойственности утверждает следующее:
Теорема 2.2: Если две формулы, не содержащие знаков импликации и эквиваленции, равносильны, то и двойственные им формулы также равносильны.
Нормальные формы
Нормальная форма – это синтаксически однозначный способ записи формулы, реализующей данную функцию.
Пользуясь известными законами логики, всякую формулу можно преобразовать в равносильную ей формулу вида 
, где 
и каждое 
– либо переменная, либо отрицание переменной, либо конъюнкция переменных или их отрицаний. Другими словами, любую формулу можно привести к равносильной ей формуле простого стандартного вида, которой будет являться дизъюнкция элементов, каждый из которых представляет собой конъюнкцию отдельных различных логических переменных либо со знаком отрицания, либо без него.
Пример 2.3: В больших формулах или при многократных преобразованиях принято знак конъюнкции опускать (по аналогии со знаком умножения): 
. Мы видим, что после проведенных преобразований формула представляет собой дизъюнкцию трех конъюнкций.
Такая форма называется дизъюнктивной нормальной формой (ДНФ). Отдельный элемент ДНФ называется элементарной конъюнкцией или конституентой единицы.
Аналогично любую формулу можно привести к равносильной ей формуле, которая будет являться конъюнкцией элементов, каждый из которых будет представлять собой дизъюнкцию логических переменных со знаком отрицания или без него. То есть, каждую формулу можно привести к равносильной ей формуле вида 
, где 
и каждое 
– либо переменная, либо отрицание переменной, либо дизъюнкция переменных или их отрицаний. Такая форма называется конъюнктивной нормальной формой (КНФ).
Пример 2.4: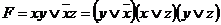 
Отдельный элемент КНФ называется элементарной дизъюнкцией или конституентой нуля.
Очевидно, что каждая формула имеет бесконечно много ДНФ и КНФ.
Пример 2.5: Найдем несколько ДНФ для формулы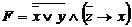 
.
1) 
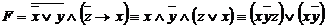
2) 
3) 
4) 
5) 
Совершенные нормальные формы
СДНФ (совершенная ДНФ) – это такая ДНФ, в которой каждая элементарная конъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные конъюнкции не повторяются.
СКНФ (совершенная КНФ) – это такая КНФ, в которой каждая элементарная дизъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные дизъюнкции не повторяются.
Пример 2.6:1) 
– СДНФ
2) 
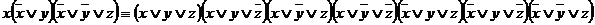1 - СКНФ
Сформулируем характерные признаки СДНФ (СКНФ).
1) Различны все члены дизъюнкции (конъюнкции);
2) Различны все члены каждой конъюнкции (дизъюнкции);
3) Ни одна конъюнкция (дизъюнкция) не содержит одновременно переменную и ее отрицание;
4) Каждая конъюнкция (дизъюнкция) содержит все переменные из числа входящих в исходную формулу.
Как мы видим, характерные признаки (но не формы!) удовлетворяют определению двойственности, поэтому достаточно разобраться с одной формой, чтобы научиться получать обе.
Из ДНФ (КНФ) с помощью равносильных преобразований легко можно получить СДНФ (СКНФ). Так как правила получения совершенных нормальных форм также являются двойственными, то подробно разберем правило получения СДНФ, а правило получения СКНФ сформулируйте самостоятельно, используя определение двойственности.
Общее правило приведения формулы к СДНФ с помощью равносильных преобразований:
Для того чтобы привести формулу F, не являющуюся тождественно ложной, к СДНФ, достаточно:
1) привести ее к какой-нибудь ДНФ;
2) удалить члены дизъюнкции, содержащие переменную вместе с ее отрицанием (если таковые имеются);
3) из одинаковых членов дизъюнкции (если таковые имеются) удалить все, кроме одного;
4) из одинаковых членов каждой конъюнкции (если такие имеются) удалить все, кроме одного;
5) если в какой-нибудь конъюнкции не содержится переменной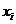 
из числа переменных, входящих в исходную формулу, добавить к этой конъюнкции член 
и применить соответствующий дистрибутивный закон;
6) если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием 3.
Полученная формула и является СДНФ данной формулы.
Пример 2.7:Найдем СДНФ и СКНФ для формулы 
.
Так как ДНФ для данной формулы уже найдена (см. Пример 2.5), то начнем с получения СДНФ:
1) ;
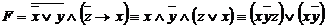2) в полученной дизъюнкции нет переменных вместе с их отрицаниями;
3) в дизъюнкции нет одинаковых членов;
4) ни в одной конъюнкции нет одинаковых переменных;
5) первая элементарная конъюнкция содержит все переменные из числа входящих в исходную формулу, а во второй элементарной конъюнкции не хватает переменной z, поэтому добавим в нее член 
и применим дистрибутивный закон: 
;
6) легко заметить, что в дизъюнкции появились одинаковые члены, поэтому убираем один (предписание 3);
Таким образом, получаем СДНФ формулы F: 
.
Для получения СКНФ воспользуемся 4 вариантом ДНФ (пример 3.3), которую можно также рассматривать как КНФ формулы: .
1) ;
2) полученная конъюнкция не содержит переменных вместе с их отрицаниями;
3) в конъюнкции нет одинаковых членов;
4) так как пока нет дизъюнкций, то в них нет и одинаковых членов;
5) получим первые элементарные дизъюнкции, добавив к переменной х конъюнкцию 
, а к переменной 
– конъюнкцию 
: 
;
6) в полученной конъюнкции имеются одинаковые члены, поэтому перейдем к предписанию 3;
3) уберем одну из одинаковых дизъюнкций: 
;
4) в оставшихся дизъюнкциях нет одинаковых членов;
5) ни в одной из элементарных дизъюнкций нет всех переменных из числа входящих в исходную формулу, поэтому дополним каждую из них конъюнкцией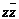 
: 
;
6) в полученной конъюнкции нет одинаковых дизъюнкций, поэтому найденная конъюнктивная форма является совершенной.
Так как в совокупности СКНФ и СДНФ формулы F 8 членов, то скорее всего они найдены верно.
Каждая выполнимая (опровержимая) формула имеет одну единственную СДНФ и одну единственную СКНФ. Тавтология не имеет СКНФ, а противоречие – СДНФ.
Дата добавления: 2018-02-28; просмотров: 27559; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!