Проверка полноты множества функций
Тема программы: Основные классы функций. Полнота множеств. Теорема Поста
Цель работы:Получение практических навыков применения теоремы Поста.
Время выполнения: 2 часа.
Теоретические основы
Теорема Поста о полноте
Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T0, T1, L, S, M.
Следствие. Всякий замкнутый класс функций из Р2, не совпадающий с Р2 содержится, по крайней мере, в одном из замкнутых классов T0, T1, L, S, M.
1. Покажем, что система функций {f1 =x1x2, f2 =0, f3 =1, f4 = x1Åx2Åx3} полна в Р2. Составим таблицу, которая называется критериальной :
2.
| Т0 | Т1 | L | M | S | |
| x1x2 | + | + | - | + | - |
| + | - | + | + | - | |
| - | + | + | + | - | |
| x1Åx2Åx3 | + | + | + | - | + |
| x1 x2 x3 | x1Åx2Åx3 |
| 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Из таблицы видно, что какой бы класс мы ни взяли, всегда есть функция из данной системы , которая в этот класс не входит. Можно сформулировать следующее правило: для того чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце критериальной таблицы был хотя бы один «минус».
Отметим еще одно обстоятельство, касающееся приведенной системы. Какую бы функцию из этой системы мы ни удалили, система станет неполной, действительно, {f2, f3, f4}ÎL, {f1, f3, f4}ÎT1, {f1, f2, f4}ÎT0, {f1, f2, f3}ÎM.
2 Мы знаем, что система {x1|x2} – полна в Р2. Составим для нее критериальная таблица? x1|x2=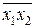 
= x1x2Å1.
|
|
|
| Т0 | Т1 | L | M | S | |
| x1|x2 | - | - | - | - | - |
3. Составим критериальную таблицу для другой полной системы функций из Р2: из Р2: {0, 1, x1x2, x1Åx2}.
| Т0 | Т1 | L | M | S | |
| + | - | + | + | - | |
| - | + | + | + | - | |
| x1x2 | + | + | - | + | - |
| x1Åx2 | + | - | + | - | - |
Согласно критериальной таблице, полной является и система {0, 1, x1x2, x1Åx2}. Константа 0 введена в эту систему для удобства, тогда мы можем записать полином Жегалкина в виде, где а 
равны 0, если члены х 
х 
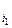...х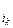 
, в полиноме отсутствуют.
4. Выясним, полна ли система 
. Составим критериальную таблицу, очевидно 
. Чтобы показать, что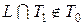 
, достаточно найти одну функцию 
и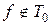 
. Возьмем 
, удовлетворяющую требуемым условиям. Если f 
S\T0, то f(0, ..., 0) = 1, f(1, ..., 1)=0, следовательно, f 
M, f T1. Рассмотрим функцию h = x1x2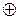 
x2x3 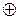x1x3=1, набор ее значений (11101000), h S\T0, но h L. Следовательно, критериальная таблица имеет вид:
| Т0 | Т1 | L | M | S | |
L  T1
| - | + | + | - | - |
| S\T0 | - | - | - | + | - |
и А – полная система функций.
Определение.Система функций {f1, ..., fs, ...} называется базисом в Р2,если она полна в Р2, но любая ее подсистема не будет полной. Например, система функций {x1&x2, 0, 1, x1 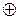x2 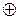x3} – базис.
Рассмотрим набор функций f, g и h, представленный в следующей таблице:
|
|
|
| Функции f, g и h | |||||
| X1 | X2 | X3 | f | g | h |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 |
Таблица 1
Функция f, очевидно, не сохраняет 0 и 1, но является самодвойственной. Функция g(X1,X2,X3)= 1+X1+X2 + X1 * X3 + X1 * X2 * X3 является несамодвойственной, немонотонной и нелинейной. По лемме 5.1 получаем, что 
, функция 
, а функция 
. Подставив X2=0 в g получим g3(X1,X3)= g(X1,0,X3)= 1 + X1 + X1 * X3. Тогда 
. Таким образом, мы с помощью f и g сумели выразить обе функции полной системы 
и, следовательно, система функций {f, g } полная.
Практические задания
Вариант 1
Задача 1. Докажите полноту системы 
, включающей только стрелку Пирса, непосредственно выразив через нее отрицание, дизъюнкцию и конъюнкцию.
Задача 2. Проверьте полноту системы функций {g, h}, представленных в таблице 1 Если она полна, выразите с помощью этих функций обе константы, отрицание 
и импликацию 
Задача 3 Докажите, что система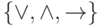 
не является полной. Можно ли ее сделать полной, добавив некоторую константу?
Вариант 2
Задача 1. Определите принадлежность каждой из функций f1, f2, f3, f4 и f5, представленных в таблице 1, каждому из классов 
и 
.
|
|
|
Задача 2 Используя результаты задачи 1, определите, какие из троек функций, представленных в таблице 5.1, являются полными системами. Имеются ли среди них полные системы из двух функций? Из одной функции?
Задача 3. Выразите функции 
с помощью формул, построенных из функций полной системы 
Контрольные вопросы
1. Полнота системы функций и критерий Поста?
2. Теорема Поста (практическое применение) ?
3.Базис системы функций ?
Список литературы
| 1.Аляев Ю.А. Тюрин С.Ф. Дискретная математика и математическая логика. — М.: Финансы и статистика, 2006. — 368 с. |
| 2.Варпаховский Ф.Л. Элементы теории алгоритмов. - М., Просвещение, 1970. - 25 с. (МГЗПИ) |
| 3.Гуц А.К. Математическая лоrика и теория алrоритмов. - Омск: Издательство Наследие. Диалог-Сибирь, 2003. - 108 с. |
| 4.Босс В. Лекции по математике. Т. 6: От Диофанта до Тьюринга. - М.: КомКнига, 2006. - 208 с. |
| 5.Босс В. Лекции по математике. Т. 10: Перебор и эффективные алгоритмы: Учебное пособие. — М.: Издательство ЛКИ, 2008. - 216 с. |
Практическое занятие №20
Дата добавления: 2018-02-28; просмотров: 1715; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!