Продольные и крутильные колебания прямых стержней
Уравнения продольных и крутильных колебаний прямого стержня.
Обозначим через  погонную массу стержня;
погонную массу стержня; 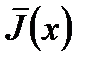 - погонный момент инерции относительно оси стержня; через
- погонный момент инерции относительно оси стержня; через  - площадь поперечного сечения;
- площадь поперечного сечения;  - экваториальный момент поперечного сечения;
- экваториальный момент поперечного сечения;  - модуль Юнга;
- модуль Юнга; 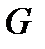 - модуль сдвига. Пусть
- модуль сдвига. Пусть  и
и 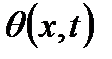 - соответственно продольное смещение и угол поворота какого-либо сечения стержня в момент
- соответственно продольное смещение и угол поворота какого-либо сечения стержня в момент  Обозначим далее через
Обозначим далее через  интенсивность внешней нагрузки – продольной, направленной по оси стержня, в случае продольных колебаний и моментной – в случае колебаний крутильных. Уравнения продольных и крутильных колебаний стержня мы получим как необходимые условия экстремума функционалов:
интенсивность внешней нагрузки – продольной, направленной по оси стержня, в случае продольных колебаний и моментной – в случае колебаний крутильных. Уравнения продольных и крутильных колебаний стержня мы получим как необходимые условия экстремума функционалов:

 (1.1)
(1.1)
для продольных колебаний и
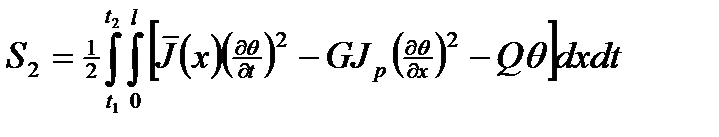 (1.2)
(1.2)
для крутильных.
Интегралы по  , взятые в пределах от 0 до
, взятые в пределах от 0 до  (длина стержня) от первого и двух последних слагаемых в квадратных скобках, представляют соответственно кинетическую и потенциальную энергию рассматриваемой системы.
(длина стержня) от первого и двух последних слагаемых в квадратных скобках, представляют соответственно кинетическую и потенциальную энергию рассматриваемой системы.
Согласно (*) необходимое условие экстремума функционала  будет иметь вид
будет иметь вид
 (1.3)
(1.3)
необходимое условие экстремума функционала 
 (1.4)
(1.4)
Условия (3) и (4) и будут уравнениями продольных и крутильных колебаний соответственно.
Когда  и жесткость
и жесткость  и
и 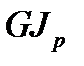 постоянны по всей длине стержня, то уравнения свободных колебаний (продольных и крутильных) однородного стержня имеют вид
постоянны по всей длине стержня, то уравнения свободных колебаний (продольных и крутильных) однородного стержня имеют вид
|
|
|
 (1.5)
(1.5)
 (1.6)
(1.6)
где 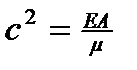 ;
;  Уравнения (5) и (6) – линейные уравнения в частных производных второго порядка с постоянными коэффициентами. Для продольных и крутильных колебаний однородного стержня они имеют одинаковую форму. Можно поэтому в общей теории ограничиться рассмотрением одного из них, например, второго, т. е. уравнения крутильных колебаний. При этом рассмотрении мы будем опираться на общий принцип линейной теории колебаний – принцип суперпозиции малых колебаний, который был положен в основу изучения колебаний систем с конечным числом степеней свободы. Мы будем предполагать, что малые колебания системы с бесконечным числом степеней свободы также представляют собой линейное наложение главных гармонических колебаний.
Уравнения (5) и (6) – линейные уравнения в частных производных второго порядка с постоянными коэффициентами. Для продольных и крутильных колебаний однородного стержня они имеют одинаковую форму. Можно поэтому в общей теории ограничиться рассмотрением одного из них, например, второго, т. е. уравнения крутильных колебаний. При этом рассмотрении мы будем опираться на общий принцип линейной теории колебаний – принцип суперпозиции малых колебаний, который был положен в основу изучения колебаний систем с конечным числом степеней свободы. Мы будем предполагать, что малые колебания системы с бесконечным числом степеней свободы также представляют собой линейное наложение главных гармонических колебаний.
Руководствуясь этим принципом, мы будем искать главные гармонические крутильные колебания стержня в таком виде:
 (1.7)
(1.7)
где  - функция, определяющая непрерывную совокупность амплитудных угловых отклонений сечений стержня от их равновесных положений. В дискретных системах с конечным числом степеней свободы эта функция вырождается в конечную совокупность амплитудных смещений сосредоточенных масс.
- функция, определяющая непрерывную совокупность амплитудных угловых отклонений сечений стержня от их равновесных положений. В дискретных системах с конечным числом степеней свободы эта функция вырождается в конечную совокупность амплитудных смещений сосредоточенных масс.
|
|
|
Подставив (7) в (6), получим уравнение собственных форм
 (1.8)
(1.8)
или

где 
Уравнение собственных форм продольных колебаний будет иметь аналогичную форму
 (1.9)
(1.9)
где 
Величины  и
и  называются иногда собственными нагрузками стержня. Применив к этим нагрузкам обобщенный принцип взаимности Рэлея, выражающийся здесь в равенстве работы нагрузки
называются иногда собственными нагрузками стержня. Применив к этим нагрузкам обобщенный принцип взаимности Рэлея, выражающийся здесь в равенстве работы нагрузки  на перемещении
на перемещении  работе нагрузки
работе нагрузки  на перемещении
на перемещении  получим условие ортогональности собственных форм крутильных колебаний. В самом деле, из равенства этих работ
получим условие ортогональности собственных форм крутильных колебаний. В самом деле, из равенства этих работ
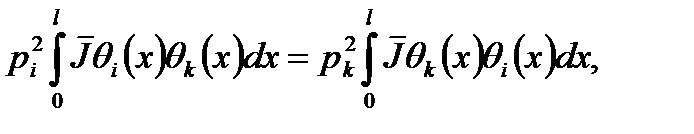
если  получим
получим
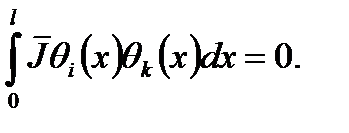 (1.10)
(1.10)
Для продольных колебаний условие ортогональности напишется аналогичным образом:
 (1.11)
(1.11)
Задача о собственных формах и частотах колебаний приводится к интегрированию обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами. Общий интеграл уравнения (8) (для крутильных колебаний) будет иметь вид
 (1.12)
(1.12)
|
|
|
или
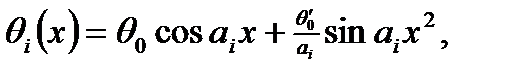
где  и
и 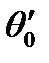 - значение угла поворота и производной от него по
- значение угла поворота и производной от него по  для
для 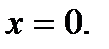 Постоянные
Постоянные  и
и 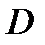 или
или  и
и 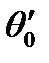 , а также собственные значения
, а также собственные значения  определяются из краевых условий задачи, т.е. из условий закрепления концов стержня. В простейших случаях концы стержня (один или оба) свободны или жестко закреплены. Эти способы закрепления выражаются следующими соотношениями:
определяются из краевых условий задачи, т.е. из условий закрепления концов стержня. В простейших случаях концы стержня (один или оба) свободны или жестко закреплены. Эти способы закрепления выражаются следующими соотношениями:
1) для крутильных колебаний на свободном конце
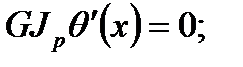 (1.13)
(1.13)
на закрепленном
 (1.14)
(1.14)
2) в случае продольных колебаний на свободном конце
 (1.15)
(1.15)
на закрепленном
 (1.16)
(1.16)
Другие свойства собственных форм аналогичны свойствам форм систем с конечным числом степеней свободы. Так, остается в силе теорема об узлах собственных форм: число узлов собственной формы  -го порядка равно
-го порядка равно  -1; при этом узлы двух последовательных форм перемежаются. Остается также в силе и теорема о разложении любой формы по собственным формам однородной задачи.
-1; при этом узлы двух последовательных форм перемежаются. Остается также в силе и теорема о разложении любой формы по собственным формам однородной задачи.
Общее решение уравнения (8) мы получим как бесконечную линейную сумму главных колебаний
|
|
|
 (1.17)
(1.17)
или
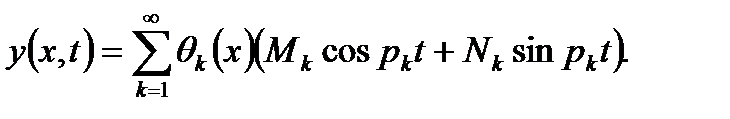 (1.18)
(1.18)
Постоянные  определяются из начальных условий, которые в случае крутильных колебаний выражаются заданием в начальный момент
определяются из начальных условий, которые в случае крутильных колебаний выражаются заданием в начальный момент  распределения по стержню угловых отклонений
распределения по стержню угловых отклонений

и их производных по 

где  и
и  - некоторые заданные функции переменной
- некоторые заданные функции переменной  .
.
Само вычисление постоянных производится следующим образом. Прежде всего находим из (18)
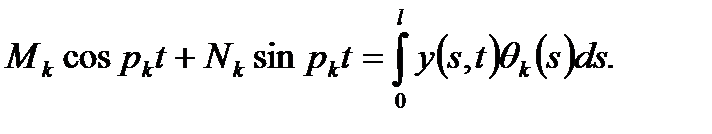

 (1.19)
(1.19)
Положив здесь  получим
получим
 (1.20)
(1.20)
Взяв производную от (19) по 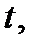 найдем
найдем
 (1.21)
(1.21)
Как видно из последней формулы, постоянные  и
и  являются коэффициентами разложения заданных функций
являются коэффициентами разложения заданных функций  и
и  по собственным формам
по собственным формам 
Частоты главных колебаний стержня образуют бесконечный дискретный ряд значений. Перенумерованные в порядке возрастания они вместе с порядковым номером растут до бесконечности.
Дата добавления: 2018-02-28; просмотров: 529; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
