Правила вычисления неопределенного интеграла

ГЛАВА 1 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ Какая операция является обратной к операции дифференцирования и какое отношение это имеет к интегрированию? Об этом мы узнаем в данной главе.

ЛЕКЦИЯ 1 Первообразная, неопределенный интеграл

Что главное мы узнали на прошлой лекции в 1-м семестре

На прошлой лекции мы закончили главу, посвященную дифференциальному исчислению функции одной переменной.

Что мы узнаем на этой лекции

Мы переходим к главе, в которой будем изучать вопросы, связанные с нахождением первообразной и интегрированием.

Понятие первообразной и неопределенного интеграла

Что такое интеграл? Правда ли, что интегрирование – это действие, обратное дифференцированию. Давайте ответим на эти и другие вопросы.

Определение 1. Первообразной для функции называется функция , такая что в области определения этих функций .

Итак, первообразная – это функция, производная от которой равна заданной функции. Заметим, что первообразная для такой функции не определяется однозначно. Например, производная от функции 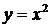равна функции 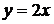. Следовательно, функция 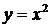является первообразной для функции 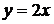. Но ведь производная от функции также равна функции . Следовательно, функция также является первообразной для функции 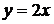, как и функция , где - произвольная постоянная. Кроме того, мы можем говорить о первообразной на некотором односвязном множестве, т. е. множестве, которое вместе с любыми двумя точками содержат отрезок, их соединяющий.

Теорема 1. (Общий вид первообразных для заданной функции) Пусть функция является первообразной для непрерывной функции на некотором односвязном множестве. Тогда любая первообразная функции представляется в виде , где - произвольная постоянная. И наоборот, при любом функция является первообразной для функции на этом множестве.

Доказательство. Вторая часть теоремы очевидна, т. к. . Теперь достаточно доказать, что, если производные двух функций равны, то эти функции отличаются на константу. По сути, достаточно доказать, что если производная от функции (разности упомянутых функций) равна 0, то это производная от константы. Но это действительно так. Возьмем любые две точки множества. Разность значений функции в этих точках по формуле конечных приращений Лагранжа равна производной в некоторой промежуточной точке, умноженной на разность аргументов ( ). Но ведь производная везде равна 0, следовательно, и приращение функции всегда равно 0, т. е. функции равна константе. Теорема доказана.

Определение 2. Совокупность всех первообразных для функции называется неопределенным интегралом от функции и обозначается символом .

Итак, действительно, вычислить неопределенный интеграл – это означает выполнение действия, обратного вычислению производной. Кроме того, с учетом теоремы 1, справедлива формула для вычисления неопределенного интеграла

, (1)

где 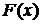- одна из первообразных для подынтегральной функции .

Мы уже знаем, что производная функции имеет многочисленные приложения. Речь в приложениях, конечно идет о значении производных в отдельных точках, т. е. о числах. Обратите внимание, что неопределенный интеграл – это совокупность функций. Поэтому непосредственное применение неопределенного интеграла весьма ограничено. В приложениях встречаются другие виды интегралов, где результатом является число, а технически вычисление сводится к нахождению первообразной функции. Поэтому очень важно научиться вычислять неопределенный интеграл – это является основой вычисления практически всех других типов интегралов.

2. От каких функций можно вычислить
неопределенный интеграл

Мы знаем, что можно вычислить производную любой элементарной функции, используя таблицу производных основных элементарных функций и правила вычисления производных (производная суммы, разности, произведения, частного, сложной функции).

Отсюда можно написать таблицу первообразных, прочитав таблицу производных «справа налево». Можно также сформулировать правила, соответствующие правилам вычисления производной. С суммой, разностью, вынесением числового множества правила дифференцирования и интегрирования идентичны. А вот с произведением, частным и вычислением производной сложной функции ситуация сложнее. Ведь производная, скажем, произведения не равна «произведению производных». Поэтому таблица первообразных и правила вычисления первообразных не позволяют найти первообразную любой элементарной функции. Существуют так называемые, «не берущиеся» интегралы от элементарных функций. Например, казалось бы, простой интеграл нельзя в нашем понимании вычислить, т. к. среди элементарных функций нет функции, производная от которой равна . Первообразная для непрерывной функции существует всегда, но в данном случае она не является элементарной. Такие функции называются специальными. Многие из них нужны в приложениях, и их изучают особо.

Итак, в отличии от вычисления производной функции, от нас не требуется умение вычислить неопределенный интеграл от любой элементарной функции, да это и невозможно. Мы изучим определенные типы элементарных функций, от которых должны научиться вычислять неопределенные интегралы.

Таблица простейших неопределенных интегралов

Давайте вспомним таблицу производных основных элементарных функций:

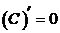
1)	2)	3)	4)
5)	6)	7)	8)
9)	10)	11)	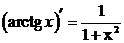12)

Во многом она порождает таблицу простейших неопределенных интегралов. Здесь есть и другие интегралы. Все они легко могут быть проверены вычислением производной от правых частей.

1)	2)	3)
4)	5)	6)
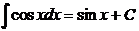
7)	8)	9)
10)	11)	12)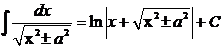
13)	14)	15)

Правила вычисления неопределенного интеграла

Правила вычисления неопределенного интеграла получены и соответствуют правилам вычисления производной.

Мы помним, что производная суммы равна сумме производных дифференцируемых функций.

Теорема 2. Пусть и . Тогда справедлива формула .

Доказательство сводится к проверке того, что производная правой части равна подынтегральной функции, что очевидно в силу условий теоремы.

Итак, интеграл от суммы интегрируемых функций равен сумме их интегралов. Аналогично справедливы следующие теоремы:

Теорема 3. Пусть и . Тогда справедлива формула .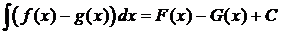

Теорема 4. Пусть , тогда справедлива формула .

Итак, для интегрируемых функций первообразная разности этих функций равна разности соответствующих первообразных, и постоянный множитель выносится при вычислении интеграла.

Производная произведения дифференцируемых функций вычисляется по формуле . Проинтегрировав обе части этого равенства, мы приходим к формуле интегрирования по частям в неопределенном интеграле.

Теорема 5. Пусть существуют и интегрируемы функци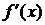и , , и . Тогда справедлива формула

. (2)

Для дифференцируемых функци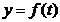й и справедлива формула , т. е. производная сложной функции равна произведению соответствующих производных. Этой формуле соответствует формула замены переменных в неопределенном интеграле.

Теорема 6. Пусть существуют, дифференцируемы и интегрируемы функции , . Тогда для значений переменной , входящей в область определения функции и в множество значений функции , справедлива формула

. (3)

Дата добавления: 2018-02-28; просмотров: 923; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!