Шаг 2 – Вычисление частных производных
Nbsp;
Оглавление
№1 – Вычислить первый и второй дифференциал функции 
в точке 
2
Теория: 2
Практика: 2
№2 – Исследовать на дифференцируемость функцию в точке 
.. 5
Теория: 5
Практика: 6
№3 – Разложить функцию в точке по формуле Тейлора до порядка 
включительно. 9
Теория: 9
Практика: 9
№4 – Исследовать на экстремум функцию.. 12
Теория: 12
Практика: 12
№5 – Найти дифференциал в точке M функции заданной неявно. 14
Практика: 14
№6 – Преобразовать уравнение, заменив независимые переменные. 15
Практика: 15
№7 – Найти производную функции f по направлению вектора 
в точке M.. 16
Практика: 16
№8 – Написать уравнение касательной плоскости к заданной поверхности в точке 17
Практика: 17
№9 – Написать уравнение нормали, проходящей через заданную точку к поверхности 18
Практика: 18
Литература: 19
№1 – Вычислить первый и второй дифференциал функции 
в точке 
Теория:
Практика:
Задание (Тип 1): 
Замечание:тут Fзависит только от одного аргумента. В заданиях функции зависят только от одного или от двух аргументов.
Шаг 1 – Найдем первый дифференциал
Пояснение:
Вспомним, что 
, поэтому в нашем примере возникает второй множитель 
. Он и есть это 
, которое мы добавляем, чтобы получить именно дифференциал, а не производную.
Шаг 2 – Подставим в найденный дифференциал точку 
Шаг 3 – Найдем второй дифференциал
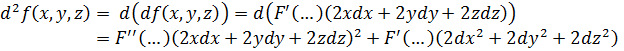
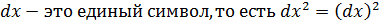
Пояснение:
Тут у нас дифференциал произведения, то есть
. У нас нужно найти такой дифференциал:
, он является произведением. Поэтому находим по формуле выше. Квадрат получился по следствию из первого пояснения. Мы записали вторую производную
, и вот из-за этого квадрата в знаменателе и возникает квадрат во втором дифференциале(чтобы сократить этот квадрат в знаменателе и получить дифференциал, а не производную)
|
|
|
Шаг 4 – Подставим во второй дифференциал точку
Замечание: теперь выполним задание для функции двух аргументов.
Задание (Тип 2): 
Пояснение: 
- производная по первому аргументу, то есть второй множитель в первом слагаемом – это как раз дифференциал первого аргумента. Для второго аргумента и слагаемого аналогично.
Замечание: для кратности будем 
обозначать как просто 
Пояснение: 
производные, взятые по первому, потом по второму аргументу и наоборот. Тут применялись все правила из пояснений выше.
№2 – Исследовать на дифференцируемость функцию в точке 
Теория:
Практика:
Замечание: в заданиях рассматриваются функции только двух переменных. Заданы они либо системой, либо просто формулой. И проверяется дифференцируемость всегда в нуле( 
).
|
|
|
Задание (Тип 1):
Точка как обычно
Шаг 1 – Пишем условие дифференцируемости
Замечание:cлева в равенстве стоит приращение функции в точке 
.
Этот критерий можно переформулировать иначе(Это более удобно для доказательства):
У нас дифференцируемость функции проверяется в точке 
, так что предел можно переписать так:
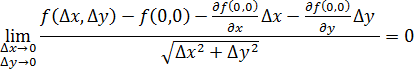
Шаг 2 – Вычисление частных производных
1. 
У нас 
по условию, значит:
2. 
Видим, что первая частная производная равна бесконечности. Из этого следует, что наша функция не дифференцируема в точке (0,0)
Задание (Тип 2):
Дата добавления: 2018-02-28; просмотров: 243; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!