Показательная форма комплексного числа
 .
.
1.2. Действия над комплексными числами
Сложение и вычитание.


Умножение.

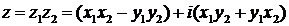
В тригонометрической форме:
 ,
, 

В случае комплексно – сопряженных чисел:

В показательной форме:
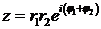
Деление.


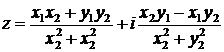
В тригонометрической форме:

В показательной форме:

Возведение в степень.
Из операции умножения комплексных чисел следует, что
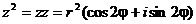 .
.
В общем случае получим:
 ,
,
где n – целое положительное число.
Это выражение называется формулой Муавра.
(Абрахам де Муавр (1667 – 1754) – английский математик)
Извлечение корня из комплексного числа.

Возводя в степень, получим:

Отсюда: 

Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
2. ПОНЯТИЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
Однозначная функция комплексной переменной  – это правило, по которому каждому комплексному значению независимой переменной z (из области определения) соответствует одно и только одно комплексное значение функции w. В теории рассматриваются также многозначные и некоторые другие типы функций, но для простоты я остановлюсь на одном определении.
– это правило, по которому каждому комплексному значению независимой переменной z (из области определения) соответствует одно и только одно комплексное значение функции w. В теории рассматриваются также многозначные и некоторые другие типы функций, но для простоты я остановлюсь на одном определении.
Функция комплексной переменной 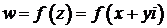 зависит от переменных x и y, которые принимают «обычные» значения.
зависит от переменных x и y, которые принимают «обычные» значения.
Функцию комплексной переменной можно записать в виде:  , где
, где 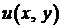 и
и  – две функции двух действительных переменных.
– две функции двух действительных переменных.
Функция 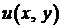 называется действительной частью функции w. Функция
называется действительной частью функции w. Функция  называется мнимой частью функции w.
называется мнимой частью функции w.
|
|
|
То есть, функция комплексной переменной  зависит от двух действительных функций
зависит от двух действительных функций 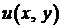 и
и  .
.
2.1. Основные элементарные функции комплексного переменного
1. Показательная функция  определяется для любого z=x+iy соотношением
определяется для любого z=x+iy соотношением
 . (2.1)
. (2.1)
Показательная функция  обладает следующими свойствами:
обладает следующими свойствами:
а)  , где z1 и z2 _- любые комплексные величины;
, где z1 и z2 _- любые комплексные величины;
б)  , т. е.
, т. е.  является периодической функцией с периодом
является периодической функцией с периодом  .
.
2. Тригонометрические функции sin z и cos z в комплексной плоскости выражаются через показательную функцию. Для функций комплексного переменного справедливы формулы Эйлера:
 ,
,  ,
,
откуда
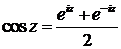 ,
, 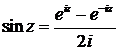 . (2.2)
. (2.2)
Функции tg z и ctg z определяются равенствами
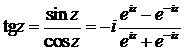 ,
,  . (2.3)
. (2.3)
Для тригонометрических функций остаются в силе все формулы тригонометрии.
3. Гиперболические функции sh z, ch z, th z, cth z в комплексной плоскости определяются равенствами
 ,
,  , (2.4)
, (2.4)
 ,
, 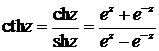 . (2.5)
. (2.5)
4. Тригонометрические и гиперболические функции связаны следующими соотношениями:
 ;
;  ;
;
 ;
; 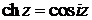 ;
;
 ;
;  ;
;
 ;
;  .
.
5. Логарифмическая функция Ln z, где  , определяется как функция, обратная к показательной, причем
, определяется как функция, обратная к показательной, причем
|
|
|

 , (2.6)
, (2.6)
где Arg z - аргумент комплексного числа z,
arg z - главное значение Arg z.
Эта функция является многозначной. Главным значением Ln z называется то значение, которое получается при k = 0; оно обозначается ln z:
 . (2.7)
. (2.7)
Очевидно, что
 ,
,  (2.8)
(2.8)
Справедливы следующие соотношения:
 ,
,  .
.
6. Обратные тригонометрические функции Arcsin z, Arccos z, Arctg z, Arcctg z определяются как функции, обратные соответственно к функциям sinω, cosω, tgω, ctg ω.
Например, если z = cosω, то ω называется арккосинусом числа z и обозначается ω = Arccos z.
Все эти функции являются многозначными и выражаются через логарифмические функции:
 ; (2.9)
; (2.9)
 ; (2.10)
; (2.10)
 ; (2.11)
; (2.11)
 . (2.12)
. (2.12)
Главные значения обратных тригонометрических функций arcsin z, arccosz, arctg z, arcctg z получаются, если брать главные значения соответствующих логарифмических функций.
7. Общая степенная функция 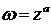 , где
, где  - любое комплексное число, определяется равенством
- любое комплексное число, определяется равенством
 . (2.13)
. (2.13)
Эта функция многозначная, ее главное значение равно
|
|
|
 .
.
8. Общая показательная функция  (
(  - любое комплексное число) определяется равенством
- любое комплексное число) определяется равенством
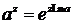 . (2.14)
. (2.14)
Главное значение этой многозначной функции  .
.
2.2. Дифференцирование функции комплексного переменного.
Условия Коши-Римана
Пусть однозначная функция f(z) определена и конечна в некоторой окрестности точки z комплексной плоскости, включая и саму точку z.
Функция f(z) называется дифференцируемой в точке z, если существует конечный предел отношения
 . (2.15)
. (2.15)
Этот предел называется производной функции f(z) в точке z.
Условие дифференцируемости функции  в терминах действительных функций
в терминах действительных функций 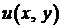 и
и  выражает следующая теорема.
выражает следующая теорема.
Теорема. Для того, чтобы функция  была дифференцируема в точке z = x + iy, необходимо и достаточно, чтобы функции
была дифференцируема в точке z = x + iy, необходимо и достаточно, чтобы функции 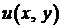 и
и  были дифференцируемы в этой точке и удовлетворяли в ней условиям Коши-Римана:
были дифференцируемы в этой точке и удовлетворяли в ней условиям Коши-Римана:
 ;
;  . (2.16)
. (2.16)
С учетом условий (2.16) производную функции f(z) можно представить в следующих равносильных формах:
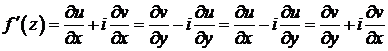 (2.17)
(2.17)
Так как обычные свойства алгебраических действий и предельного перехода сохраняются при переходе к функциям комплексного переменного, то сохраняются и обычные правила дифференцирования:
|
|
|
 ,
,  ,
,
 ,
,  ,
,  .
.
В последней формуле f и φ обозначают взаимно обратные функции, осуществляющие однолистные отображения соответственно точек z и 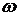 .
.
Функция  называется аналитической в данной точке z ∈ D, если она дифференцируема как в самой точке z, так и в некоторой ее окрестности.
называется аналитической в данной точке z ∈ D, если она дифференцируема как в самой точке z, так и в некоторой ее окрестности.
Функция f(z) называется аналитической в области D, если она дифференцируема в каждой точке этой области.
Производные элементарных функций  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 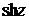 ,
,  находятся по тем же формулам, что и для действительного аргумента:
находятся по тем же формулам, что и для действительного аргумента:
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
Если для функции 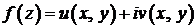 в области D функции
в области D функции 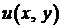 и
и  непрерывны, то выполнение условий (2.16) достаточно для того, чтобы данная функция была аналитической в этой области, причем в любой точке z∈D производная аналитической функции может быть найдена по правилам дифференцирования функции действительной переменной.
непрерывны, то выполнение условий (2.16) достаточно для того, чтобы данная функция была аналитической в этой области, причем в любой точке z∈D производная аналитической функции может быть найдена по правилам дифференцирования функции действительной переменной.
3. РЕШЕНИЕ ТИПОВОГО ВАРИАНТА ПО ДИСЦИПЛИНЕ
«ФУНКЦИИ КОМПЛЕКСОНОГО ПЕРЕМЕННОГО»
Задание №1. Даны два комплексных числа, записанных в алгебраической форме z1 = 5 + 2 i и z2 = 3 – 4 i. Найти:
а) z1+ z2; б) z1– z2
в) z1 × z2; г) z1: z2,
Решение:
а) z1+ z2 = (5 + 2 i) +(3 – 4 i) = 8 – 2 i
б) z1– z2= (5 + 2 i) – (3 – 4 i) = 2 +6 i
в) z1 × z2 = (5 + 2 i) +(3 – 4 i) = 15 – 20 i + 6 i – 8 i2.
Учитывая, что i2= – 1, получим z1 × z2 = 23 – 14 i
г)  =
=  . Умножим числитель и знаменатель на сопряженное знаменателю комплексное число (3 + 4 i), получим:
. Умножим числитель и знаменатель на сопряженное знаменателю комплексное число (3 + 4 i), получим:
 =
=  =
=  = 0.28 + 1.04i.
= 0.28 + 1.04i.
Задание №2. Записать число  в алгебраической форме.
в алгебраической форме.
Решение:
Воспользуемся тем, что
i4×k = 1 i4×k +1= i
i4×k +2= i2= –1 i4×k +3= i3 = – i, тогда
i 34 = i4×8 +2 = i2 = –1,
i 53 = i4×13 +1 = i,
i76 = i4×19 = 1, поэтому заданное число z принимает вид:
 .
.
Аналогично заданию 1(г) умножим числитель и знаменатель на сопряженное знаменателю комплексное число
(–4– 5 i), получим:
z = 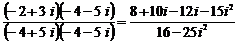 =
=  =
=  –
– 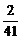 i.
i.
Задание №3. Представить числа в тригонометрической и показательной форме.
а) z = – 5 + 5 i б) z = 3 i
Решение:
а) Найдем модуль комплексного числа z:
r = ïz ç=  =
= 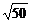 = 5
= 5  .
.
Из соотношений cosj =  и sinj =
и sinj =  , получаем аргумент числа z (берем главное значение аргумента): j =
, получаем аргумент числа z (берем главное значение аргумента): j =  . Тогда z = 5
. Тогда z = 5  (cos
(cos  + +i sin
+ +i sin  ) – тригонометрическая форма комплексного числа. Запишем показательную форму комплексного числа: z = 5
) – тригонометрическая форма комплексного числа. Запишем показательную форму комплексного числа: z = 5 
 .
.
б) Аналогично, модуль комплексного числа z:
r = ïz ç=  = 3, cosj =
= 3, cosj =  = 0 и sinj =
= 0 и sinj = 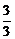 = 1, получаем Arg z= j =
= 1, получаем Arg z= j =  , т.е. z = 3 (cos
, т.е. z = 3 (cos  +i sin
+i sin  ) – тригонометрическая форма комплексного числа и z = 3
) – тригонометрическая форма комплексного числа и z = 3  – показательная форма комплексного числа.
– показательная форма комплексного числа.
Задание №4. Даны два числа z1 = 5 (cos  + i sin
+ i sin  ).
).
и z2= 3 (cos  + i sin
+ i sin  ), записанные в тригонометрической форме. Найти: а) z1× z2; б)
), записанные в тригонометрической форме. Найти: а) z1× z2; б)  ; в) z17; г)
; в) z17; г)  .
.
Решение:
а) Так как при умножении комплексных чисел, записанных в тригонометрической форме, их модули перемножаются, а аргументы складываются, получаем:
z1× z2 = 5×3×  =15
=15  .
.
б) При нахождении частного двух комплексных чисел, записанных в тригонометрической форме модуль полученного числа равен частному модулей этих чисел, а аргумент равен разности их аргументов.
 =
= 
 =
= 
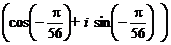 .
.
в) Для возведения числа z1 в седьмую (натуральную) степень, применим формулу Муавра:
[r (cosj + i sinj)]n = rn (cosnj + i sinnj).
Получим:
z17=  = 57
= 57  .
.
г) Для извлечения корня из комплексного числа используем формулу:

 , где k = 0, 1,…,(n – 1).
, где k = 0, 1,…,(n – 1).
Далее при k = n, п + 1,… значения будут повторяться. Таким образом, корень п-ой степени из комплексного числа (не равного нулю) имеет п различных значений.
Имеем:
 =
= 
 , где k = 0, 1, 2 и 3.
, где k = 0, 1, 2 и 3.
Откуда получаем четыре значения корня:
при k = 0 получаем 
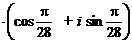 ,
,
при k = 1 получаем 
 ,
,
при k = 2 получаем 
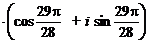 ,
,
при k = 3 получаем 
 .
.
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки, расположенные на окружности радиуса  , т.е. соответствуют вершинам правильного четырехугольника (квадрата) вписанного в окружность радиуса
, т.е. соответствуют вершинам правильного четырехугольника (квадрата) вписанного в окружность радиуса  с центром в начале координат.
с центром в начале координат.
Задание №5. Изобразить множество точек комплексной плоскости, удовлетворяющих отношениям:

Решение:
Поскольку z = х + у i, тогда условие 2 £ Im z < 4, эквивалентно неравенству 2 £ у < 4 и задает бесконечную горизонтальную полосу между прямыми у = 2 и у = 4, включая нижнюю прямую у = 2 (Рис. 2.1).
Условие çz – (2 + i)ï£ 3 задает круг с центром в точке (2; 1) и радиусом равным 3, включая ограничивающую его окружность (Рис. 2.2).
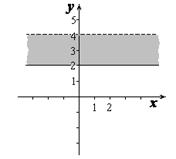

Рис. 2.1. Рис. 2.2.
Тогда получаем множество точек комплексной плоскости, удовлетворяющих заданным отношениям (Рис. 2.3).

Рис. 2.3.
Задание №6. Для функции f(z)= (`z )2 найти действительную Re(f(z)) и мнимую Im(f(z)) части.
Решение:
Полагая z = х + у i, получим `z = х – у i, тогда
f(z)= (`z )2 =(х – у i)2 = х2 –2 х у i + (у i)2 = (х2– у2) + (– 2 х у) i,
откуда имеем: Re(f(z)) = (х2– у2) и Im(f(z)) = – 2 х у.
Задание №7. Показать, что функция f(z) = z2 + z i является аналитической. Найти производную этой функции.
Решение:
Напомним определение аналитической функции:
Определение. Функция f(z) называется аналитической (иначе, регулярной или голоморфной) в области D, если она однозначно определена и дифференцируема в каждой точке этой области.
Таким образом, для выяснения аналитичности функции необходимо проверить выполнение условий Коши-Римана (условия дифференцируемости функции): 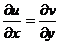 и
и  , где и(х, у) – действительная часть функции комплексного переменного и v(х, у) – мнимая.
, где и(х, у) – действительная часть функции комплексного переменного и v(х, у) – мнимая.
Функция f(z) = z2 + z i, всюду определенная на комплексной плоскости и т.к. z = х + у i, получаем:
f(z) = z2 + z i = (х + у i)2 + (х + у i)×i = (х2 – у2 – у) + (2х у +х) i, т.е.
и(х, у) = х2 – у2 – у v(х, у) = 2х у +х.
Найдем частные производные действительных функций и(х, у) и v(х, у): 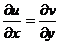 = 2х и
= 2х и  = – 2у – 1, т.е. условия Коши-Римана для функции f(z) = z2 + z i выполняются во всех точках комплексной плоскости, в силу чего она дифференцируема, а значит и аналитична во всей плоскости.
= – 2у – 1, т.е. условия Коши-Римана для функции f(z) = z2 + z i выполняются во всех точках комплексной плоскости, в силу чего она дифференцируема, а значит и аналитична во всей плоскости.
Найдем производную этой функции, применяя одно из следующих соотношений:
f¢(z) =  =
=  =
=  =
=  ,
,
получаем: f¢(z) = 2х + (2у+ 1) i = 2(х + у i) +i = 2 z + i., таким образом: (z2 + z i)¢ = 2 z + i.
Задание №8. Вычислить интеграл  , где АВ – отрезок А(0, 0) и В(1, 4).
, где АВ – отрезок А(0, 0) и В(1, 4).
Решение:
Запишем параметрическое уравнения отрезка прямой, соединяющей точки А(0, 0) и В(1, 4):
 ,
,
тогда z = х + у i = (1 + 4i)×t, где параметр t изменяющийся от 0 до 1.
Для вычисления интеграла воспользуемся формулой:
 , получим:
, получим:
 =
=  =
=
= 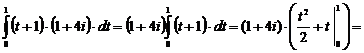
= (1 + 4i)× 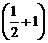 =1.5 + 6 i.
=1.5 + 6 i.
Задание №9. Вычислить интеграл I =  по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши, если g: ïz – 2ç= 1.5.
по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши, если g: ïz – 2ç= 1.5.
Решение:
Функция f(z) =  аналитична в круге g:ïz – 2 ç= 1.5, поэтому, применяя формулу Коши, находим:
аналитична в круге g:ïz – 2 ç= 1.5, поэтому, применяя формулу Коши, находим:
 =
=  = f (3) =
= f (3) =  .
.
Задание №10. Разложить функцию f(z) =  в ряд Лорана в кольце 1<½z½< 3.
в ряд Лорана в кольце 1<½z½< 3.
Решение:
Представим функцию f(z) в виде суммы простейших алгебраических дробей:
f(z) =  =
=  =
=  =
=
=  , откуда имеем систему
, откуда имеем систему
 , решая которую, получаем А= –
, решая которую, получаем А= –  и В =
и В =  , а тогда f(z) =
, а тогда f(z) =  = –
= –  ×
×  +
+  ×
×  . Принимая во внимание, что 1<½z½< 3, преобразуем f(z) = –
. Принимая во внимание, что 1<½z½< 3, преобразуем f(z) = –  ×
× 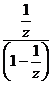 –
–  ×
×  .
.
Следовательно, f(z) = –  ×
× 

Задание №11. Охарактеризовать особую точку для указанной функции:
а) f(z) = 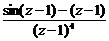 б) f(z) =
б) f(z) =  .
.
Решение:
а) Точка z0 = 1 является особой для данной функции. Воспользуемся разложением функции sin(z –1) в ряд:
sin(z–1) = (z–1) –  +
+  –
–  +…, тогда
+…, тогда
f(z) = 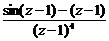 = –
= –  +
+  –
–  +
+  …
…
Т.к. разложение в ряд Лорана содержит в своей главной части лишь конечное число членов  , то z0 – полюс кратности т, а в нашем случае т = 1, следовательно, z0 = 1 является простым полюсом.
, то z0 – полюс кратности т, а в нашем случае т = 1, следовательно, z0 = 1 является простым полюсом.
б) Точка z0 = 0 является особой для данной функции. Воспользуемся разложением функции e t в ряд:
et = 1+ t +  +
+  + …, тогда
+ …, тогда
 = z2 +
= z2 +  +
+  + …
+ …
и f(z) =  =
=  +
+  +
+  + …, таким образом, разложение в ряд Лорана не содержит главной части, т.е. точка z0 = 0 является устранимой особой точкой.
+ …, таким образом, разложение в ряд Лорана не содержит главной части, т.е. точка z0 = 0 является устранимой особой точкой.
Задание №12. Найти все вычеты для данных функции.
f(z) =  .
.
Решение:
Определим особые точки функции f(z) и типы полюсов в этих точках. У функции f(z) три особые точки: z0 = 3i, z1 = 2i, z2 = 5. Точки z0 и z1 являются простыми полюсами, точка z2 является полюсом кратности 2. Найдем вычеты в этих точках:

Задание №13. Вычислить интеграл, применяя вычеты,
 .
.
Решение:
 = 2pi×
= 2pi× 
Найдем особые точки, попадающие в круг │z +3│=4: z1=2i, z2= –2i и z3=5.

 = 2pi×
= 2pi×  =
=
 .
.
4. ВАРИАНТЫ ЗАДАНИЙ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Вариант 1.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 1 – 2 i, z2 = 2 +3 i.
, если z1 = 1 – 2 i, z2 = 2 +3 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 4 – 4 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 2 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 3; n = 5.
); m = 3; n = 5.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданной функции
f(z): f(z) = cos (1 + 2z).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) =  .
.
8. Вычислить интеграл  .
.
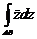 , где АВ – отрезок А(0, 0) и В (1, 2).
, где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 5.
g: ïz ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z÷ <
÷ z÷ <  .
.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
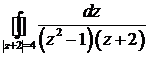 .
.
Вариант 2.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 4 – i, z2 = 3 + 2 i.
, если z1 = – 4 – i, z2 = 3 + 2 i.
2. Записать число z в алгебраической форме: 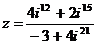 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 2– 2  i.
i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 4 (cos  + i sin
+ i sin  ); z2 = 5 (cos
); z2 = 5 (cos  + i sin
+ i sin  ); m = 5; n = 4.
); m = 5; n = 4.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z2 + z.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = sin (z3 +i).
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 3).
где АВ – отрезок А(0, 0) и В (1, 3).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I = 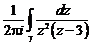 g: ïz – i ç= 5.
g: ïz – i ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  1<÷ z÷ <2.
1<÷ z÷ <2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 3.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 2 + 5 i, z2 = – 1 – 4 i.
, если z1 = 2 + 5 i, z2 = – 1 – 4 i.
2. Записать число z в алгебраической форме: 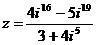 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 1 + i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = (cos  + i sin
+ i sin  ); z2 = 2 (cos
); z2 = 2 (cos  + i sin
+ i sin  ); m = 4; n = 4.
); m = 4; n = 4.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = 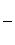
 .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = cos (z2+  +1).
+1).
8. Вычислить интеграл  .
.
 где АВ – часть кривой у = х2 от А(0, 0) до В (2, 4).
где АВ – часть кривой у = х2 от А(0, 0) до В (2, 4).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 1 ç= 2.
g: ïz – 1 ç= 2.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  1<÷ z÷<3.
1<÷ z÷<3.
11. Охарактеризовать особую точку данной функции: f(z) = 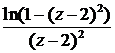 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
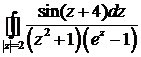 .
.
Вариант 4.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 2 +3 i, z2 = 3 + 5 i.
, если z1 = – 2 +3 i, z2 = 3 + 5 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 3 + 3  i.
i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 3 (cos  + i sin
+ i sin  ); z2 = 2 (cos
); z2 = 2 (cos  + i sin
+ i sin  ); m = 6; n = 4.
); m = 6; n = 4.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) =  .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z3 + 2 z.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I = 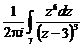 g: ïz – 3 ç= 4.
g: ïz – 3 ç= 4.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  2<÷ z÷<5.
2<÷ z÷<5.
11. Охарактеризовать особую точку данной функции: f(z) = 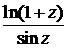 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 5.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 5 – 4 i, z2 = 6 + 4 i.
, если z1 = 5 – 4 i, z2 = 6 + 4 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = – 5  + 5 i.
+ 5 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 =5 (cos  + i sin
+ i sin  ); z2 = 6 (cos
); z2 = 6 (cos  + i sin
+ i sin  ); m = 10; n = 5.
); m = 10; n = 5.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = sin (`z + 1).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) =  .
.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 1).
где АВ – отрезок А(0, 0) и В (1, 1).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 4.
g: ïz ç= 4.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  4<÷ z÷<7.
4<÷ z÷<7.
11. Охарактеризовать особую точку данной функции: f(z) = 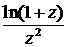 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 6.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 1 – 6 i, z2 = 2 – 7 i.
, если z1 = – 1 – 6 i, z2 = 2 – 7 i.
2. Записать число z в алгебраической форме: 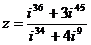 .
.
3. Представить число в тригонометрической и показательной формах:
z =  – i.
– i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 7 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 5; n = 6.
); m = 5; n = 6.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z + (`z )2.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = (i z)3.
8. Вычислить интеграл  .
.
 где АВ – часть кривой у = х2от А(0, 0) до В(1, 1).
где АВ – часть кривой у = х2от А(0, 0) до В(1, 1).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 7.
g: ïz ç= 7.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  2<÷ z – 4÷<3.
2<÷ z – 4÷<3.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 7.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 3 + 4 i, z2 = – 4 + i.
, если z1 = 3 + 4 i, z2 = – 4 + i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = – 2 – 2 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 2 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 8; n = 6.
); m = 8; n = 6.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = (`z )3.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = 4z3 – z.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 1 ç= 3.
g: ïz – 1 ç= 3.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z÷ > 3.
÷ z÷ > 3.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 8.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = –7 – 3 i, z2 = – 2 + 3 i.
, если z1 = –7 – 3 i, z2 = – 2 + 3 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 2  + 2 i.
+ 2 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 3 (cos  + i sin
+ i sin  ); z2 = 8 (cos
); z2 = 8 (cos  + i sin
+ i sin  ); m = 9; n = 6.
); m = 9; n = 6.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z3 + 2.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z4 + iz.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 5.
g: ïz ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) = 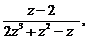 ÷ z÷ >
÷ z÷ >  .
.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
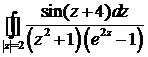 .
.
Вариант 9.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 1 + 2 i, z2 = 3 + 5 i.
, если z1 = – 1 + 2 i, z2 = 3 + 5 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = – 3  – 3 i.
– 3 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 4 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 5; n = 4.
); m = 5; n = 4.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) =  .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z×  .
.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 3).
где АВ – отрезок А(0, 0) и В (1, 3).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 2ç= 1.5.
g: ïz – 2ç= 1.5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z + 1÷ > 2.
÷ z + 1÷ > 2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 10.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 5 – 2 i, z2 = 2 + 4 i.
, если z1 = 5 – 2 i, z2 = 2 + 4 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = – 5 + 5 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 5 (cos  + i sin
+ i sin  ); z2 = (cos
); z2 = (cos  + i sin
+ i sin  ); m = 8; n = 4.
); m = 8; n = 4.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = sin (i z2).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z4 + 5z – iz.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 3.
g: ïz ç= 3.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z + 5÷ > 2.
÷ z + 5÷ > 2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 11.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 1 – 2 i, z2 = 2 +3 i.
, если z1 = 1 – 2 i, z2 = 2 +3 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 2.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 2 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 5; n = 3.
); m = 5; n = 3.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданной функции
f(z): f(z) = cos (1 + 2z).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) =  .
.
8. Вычислить интеграл  .
.
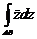 , где АВ – отрезок А(0, 0) и В (1, 2).
, где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 5.
g: ïz ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z÷ <
÷ z÷ <  .
.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
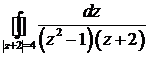 .
.
Вариант 12.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 4 – i, z2 = 3 + 2 i.
, если z1 = – 4 – i, z2 = 3 + 2 i.
2. Записать число z в алгебраической форме: 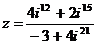 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 4 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 4 (cos  + i sin
+ i sin  ); z2 = 5 (cos
); z2 = 5 (cos  + i sin
+ i sin  ); m = 4; n = 5.
); m = 4; n = 5.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z2 + z.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = sin (z3 +i).
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 3).
где АВ – отрезок А(0, 0) и В (1, 3).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I = 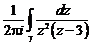 g: ïz – i ç= 5.
g: ïz – i ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  1<÷ z÷ <2.
1<÷ z÷ <2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 13.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 2 + 5 i, z2 = – 1 – 4 i.
, если z1 = 2 + 5 i, z2 = – 1 – 4 i.
2. Записать число z в алгебраической форме: 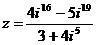 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 3.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = (cos  + i sin
+ i sin  ); z2 = 2 (cos
); z2 = 2 (cos  + i sin
+ i sin  ); m = 4; n = 4.
); m = 4; n = 4.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = 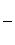
 .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = cos (z2+  +1).
+1).
8. Вычислить интеграл  .
.
 где АВ – часть кривой у = х2 от А(0, 0) до В (2, 4).
где АВ – часть кривой у = х2 от А(0, 0) до В (2, 4).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 1 ç= 2.
g: ïz – 1 ç= 2.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  1<÷ z÷<3.
1<÷ z÷<3.
11. Охарактеризовать особую точку данной функции: f(z) = 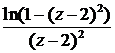 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
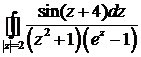 .
.
Вариант 14.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 2 +3 i, z2 = 3 + 5 i.
, если z1 = – 2 +3 i, z2 = 3 + 5 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 5 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 3 (cos  + i sin
+ i sin  ); z2 = 2 (cos
); z2 = 2 (cos  + i sin
+ i sin  ); m = 5; n = 2.
); m = 5; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) =  .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z3 + 2 z.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I = 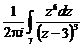 g: ïz – 3 ç= 4.
g: ïz – 3 ç= 4.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  2<÷ z÷<5.
2<÷ z÷<5.
11. Охарактеризовать особую точку данной функции: f(z) = 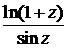 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 15.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 5 – 4 i, z2 = 6 + 4 i.
, если z1 = 5 – 4 i, z2 = 6 + 4 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 7.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 =5 (cos  + i sin
+ i sin  ); z2 = 6 (cos
); z2 = 6 (cos  + i sin
+ i sin  ); m = 10; n = 2.
); m = 10; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = sin (`z + 1).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) =  .
.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 1).
где АВ – отрезок А(0, 0) и В (1, 1).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 4.
g: ïz ç= 4.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  4<÷ z÷<7.
4<÷ z÷<7.
11. Охарактеризовать особую точку данной функции: f(z) = 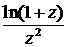 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 16.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 1 – 6 i, z2 = 2 – 7 i.
, если z1 = – 1 – 6 i, z2 = 2 – 7 i.
2. Записать число z в алгебраической форме: 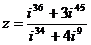 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 2 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 7 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 5; n = 2.
); m = 5; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z + (`z )2.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = (i z)3.
8. Вычислить интеграл  .
.
 где АВ – часть кривой у = х2от А(0, 0) до В(1, 1).
где АВ – часть кривой у = х2от А(0, 0) до В(1, 1).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 7.
g: ïz ç= 7.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  2<÷ z – 4÷<3.
2<÷ z – 4÷<3.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 17.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 3 + 4 i, z2 = – 4 + i.
, если z1 = 3 + 4 i, z2 = – 4 + i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z =6 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 2 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 8; n = 3.
); m = 8; n = 3.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = (`z )3.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = 4z3 – z.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 1 ç= 3.
g: ïz – 1 ç= 3.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z÷ > 3.
÷ z÷ > 3.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 18.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = –7 – 3 i, z2 = – 2 + 3 i.
, если z1 = –7 – 3 i, z2 = – 2 + 3 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 4.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 3 (cos  + i sin
+ i sin  ); z2 = 8 (cos
); z2 = 8 (cos  + i sin
+ i sin  ); m = 9; n = 3.
); m = 9; n = 3.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z3 + 2.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z4 + iz.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 5.
g: ïz ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) = 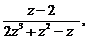 ÷ z÷ >
÷ z÷ >  .
.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
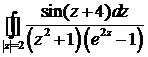 .
.
Вариант 19.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 1 + 2 i, z2 = 3 + 5 i.
, если z1 = – 1 + 2 i, z2 = 3 + 5 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 4 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 5; n = 2.
); m = 5; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) =  .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z×  .
.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 3).
где АВ – отрезок А(0, 0) и В (1, 3).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 2ç= 1.5.
g: ïz – 2ç= 1.5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z + 1÷ > 2.
÷ z + 1÷ > 2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 20.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 5 – 2 i, z2 = 2 + 4 i.
, если z1 = 5 – 2 i, z2 = 2 + 4 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = – 6.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 5 (cos  + i sin
+ i sin  ); z2 = (cos
); z2 = (cos  + i sin
+ i sin  ); m = 9; n = 2.
); m = 9; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = sin (i z2).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z4 + 5z – iz.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 3.
g: ïz ç= 3.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z + 5÷ > 2.
÷ z + 5÷ > 2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 21.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 1 – 2 I, z2 = 2 +3 i.
, если z1 = 1 – 2 I, z2 = 2 +3 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 2i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 2 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 3; n = 2.
); m = 3; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданной функции
f(z): f(z) = cos (1 + 2z).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) =  .
.
8. Вычислить интеграл  .
.
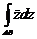 , где АВ – отрезок А(0, 0) и В (1, 2).
, где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 5.
g: ïz ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z÷ <
÷ z÷ <  .
.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
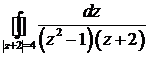 .
.
Вариант 22.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 4 – i, z2 = 3 + 2 i.
, если z1 = – 4 – i, z2 = 3 + 2 i.
2. Записать число z в алгебраической форме: 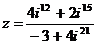 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 4 i+4.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 4 (cos  + i sin
+ i sin  ); z2 = 5 (cos
); z2 = 5 (cos  + i sin
+ i sin  ); m = 6; n = 2.
); m = 6; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z2 + z.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = sin (z3 +i).
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 3).
где АВ – отрезок А(0, 0) и В (1, 3).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I = 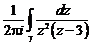 g: ïz – i ç= 5.
g: ïz – i ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  1<÷ z÷ <2.
1<÷ z÷ <2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 23.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 2 + 5 i, z2 = – 1 – 4 i.
, если z1 = 2 + 5 i, z2 = – 1 – 4 i.
2. Записать число z в алгебраической форме: 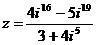 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 3+3i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = (cos  + i sin
+ i sin  ); z2 = 2 (cos
); z2 = 2 (cos  + i sin
+ i sin  ); m = 8; n = 3.
); m = 8; n = 3.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = 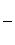
 .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = cos (z2+  +1).
+1).
8. Вычислить интеграл  .
.
 где АВ – часть кривой у = х2 от А(0, 0) до В (2, 4).
где АВ – часть кривой у = х2 от А(0, 0) до В (2, 4).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 1 ç= 2.
g: ïz – 1 ç= 2.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  1<÷ z÷<3.
1<÷ z÷<3.
11. Охарактеризовать особую точку данной функции: f(z) = 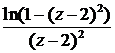 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
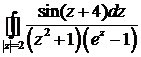 .
.
Вариант 24.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 2 +3 i, z2 = 3 + 5 i.
, если z1 = – 2 +3 i, z2 = 3 + 5 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 5+5 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 3 (cos  + i sin
+ i sin  ); z2 = 2 (cos
); z2 = 2 (cos  + i sin
+ i sin  ); m = 14; n = 2.
); m = 14; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) =  .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z3 + 2 z.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I = 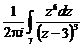 g: ïz – 3 ç= 4.
g: ïz – 3 ç= 4.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  2<÷ z÷<5.
2<÷ z÷<5.
11. Охарактеризовать особую точку данной функции: f(z) = 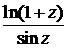 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 25.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 5 – 4 i, z2 = 6 + 4 i.
, если z1 = 5 – 4 i, z2 = 6 + 4 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 7 + 7i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 =5 (cos  + i sin
+ i sin  ); z2 = 6 (cos
); z2 = 6 (cos  + i sin
+ i sin  ); m = 8; n = 3.
); m = 8; n = 3.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = sin (`z + 1).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) =  .
.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 1).
где АВ – отрезок А(0, 0) и В (1, 1).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 4.
g: ïz ç= 4.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  4<÷ z÷<7.
4<÷ z÷<7.
11. Охарактеризовать особую точку данной функции: f(z) = 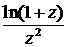 .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 26.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 1 – 6 i, z2 = 2 – 7 i.
, если z1 = – 1 – 6 i, z2 = 2 – 7 i.
2. Записать число z в алгебраической форме: 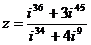 .
.
3. Представить число в тригонометрической и показательной формах:
z = – 2 – 2 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 7 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 16; n = 2.
); m = 16; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z + (`z )2.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = (i z)3.
8. Вычислить интеграл  .
.
 где АВ – часть кривой у = х2от А(0, 0) до В(1, 1).
где АВ – часть кривой у = х2от А(0, 0) до В(1, 1).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 7.
g: ïz ç= 7.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  2<÷ z – 4÷<3.
2<÷ z – 4÷<3.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 27.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 3 + 4 i, z2 = – 4 + i.
, если z1 = 3 + 4 i, z2 = – 4 + i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z =6 – 6 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 2 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 8; n = 2.
); m = 8; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = (`z )3.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = 4z3 – z.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 1 ç= 3.
g: ïz – 1 ç= 3.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z÷ > 3.
÷ z÷ > 3.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 28.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = –7 – 3 i, z2 = – 2 + 3 i.
, если z1 = –7 – 3 i, z2 = – 2 + 3 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = 4 + 4i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 3 (cos  + i sin
+ i sin  ); z2 = 8 (cos
); z2 = 8 (cos  + i sin
+ i sin  ); m = 10; n = 3.
); m = 10; n = 3.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = z3 + 2.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z4 + iz.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 5.
g: ïz ç= 5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) = 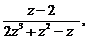 ÷ z÷ >
÷ z÷ >  .
.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
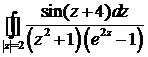 .
.
Вариант 29.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = – 1 + 2 i, z2 = 3 + 5 i.
, если z1 = – 1 + 2 i, z2 = 3 + 5 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 4 (cos  + i sin
+ i sin  ); z2 = 3 (cos
); z2 = 3 (cos  + i sin
+ i sin  ); m = 16; n = 2.
); m = 16; n = 2.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) =  .
.
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z×  .
.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 3).
где АВ – отрезок А(0, 0) и В (1, 3).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz – 2ç= 1.5.
g: ïz – 2ç= 1.5.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z + 1÷ > 2.
÷ z + 1÷ > 2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
Вариант 30.
1. Даны два числа z1и z2, записанные в алгебраической форме.
Найти: а) z1+ z2; б) z1– z2; в) z1 × z2; г)  , если z1 = 5 – 2 i, z2 = 2 + 4 i.
, если z1 = 5 – 2 i, z2 = 2 + 4 i.
2. Записать число z в алгебраической форме:  .
.
3. Представить число в тригонометрической и показательной формах:
z = – 6 + 6 i.
4. Даны два числа z1и z2, записанные в тригонометрической форме. Найти z1m;  , где:
, где:
z1 = 5 (cos  + i sin
+ i sin  ); z2 = (cos
); z2 = (cos  + i sin
+ i sin  ); m = 9; n = 3.
); m = 9; n = 3.
5. Изобразить множество точек комплексной плоскости, удовлетворяющих указанным отношениям: 
6. Найти Re(f(z)) и Im(f(z)) для заданных функций f(z):
f(z) = sin (i z2).
7. Показать, что данная функция является аналитической. Найти производную этой функции:
f(z) = z4 + 5z – iz.
8. Вычислить интеграл  .
.
 где АВ – отрезок А(0, 0) и В (1, 2).
где АВ – отрезок А(0, 0) и В (1, 2).
9. Вычислить интеграл по замкнутому контуру g, пробегаемому против часовой стрелки, применяя интегральные формулы Коши:
I =  g: ïz ç= 3.
g: ïz ç= 3.
10. Разложить функцию в ряд Лорана в данной области:
f(z) =  ÷ z + 5÷ > 2.
÷ z + 5÷ > 2.
11. Охарактеризовать особую точку данной функции: f(z) =  .
.
12. Найти все вычеты для данной функции:
f(z) =  .
.
13. Вычислить интеграл:
 .
.
ЛИТЕРАТУРА
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 2. М.: Оникс 21 век, Мир и Образование, 2007. 304 c.
2. Ильина И.В. Теория функции комплексного переменного. Операционное исчисление. / И.В. Ильина, А.А. Чермошенцева. Петропавловск-Камчатский: КамчатГТУ, 2006.
3. Пантелеев А.В., Якимова А.С. Теория функций комплексного переменного и операционное исчисление в примерах и задачах. М.: ысш. шк., 2007. 445 с.
Обухова Галина Александровна
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Методическое пособие для самостоятельной работы студентов направления «Электроэнергетика и электротехника» заочной формы обучения
Редактор Е.Ф. Изотова
Подписано к печати __.__.__. Формат 60х84/16.
Усл. печ. л. 3. Тираж 50 экз. Зак.______ Рег. № ___.
Отпечатано в ИТО Рубцовского индустриального института
658207, Рубцовск, ул. Тракторная, 2/6.
Дата добавления: 2018-02-28; просмотров: 440; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
