На электродах протекают реакции 3 страница

⇐ ПредыдущаяСтр 3 из 23Следующая ⇒

В начальный момент (рис. 3.1) газ занимает объем V1 и находится под давлением Р1. На графике такое состояние обозначено как начальное состояние 1.

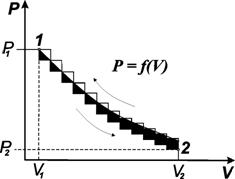
Рис. 3.1. Соотношение между Р_внеш и V, позволяющее определять работу расширения для газа, расширяющегося против постоянного внешнего давления Р₂ и против переменного давления Р

Начнем изменять давление бесконечно малыми шагами. Если оно будет падать, то объем будет возрастать также бесконечно малыми шагами. Таким путем можно перейти из состояния 1 в состояние 2, в котором газ будет иметь давление Р2 и объем V2. Графически этот бесконечно медленный процесс изображается плавной кривой 2. Работа, совершаемая системой, ограничена изотермой с ординатами Р1 и Р2 и отрезком на оси абсцисс V2 – V1 . Это работа расширения газа. Обозначим ее W1-2. Представим себе обратный процесс, в котором мы будем путем бесконечно малого увеличения давления сжимать газ. В конечном счете мы сможем вернуть его в первоначальное состояние 1. Графически этот процесс будет описываться той же плавной кривой 2-1, но протекать в обратном направлении.

В этом случае система при переходе из конечного состояния в начальное будет проходить через те же промежуточные состояния давления и объема как в прямом, так и в обратном процессах. Изменения происходили на бесконечно малые величины, и система в каждый момент времени находилась в равновесном состоянии. В этом случае работа, которую совершает система в обратном процессе W2-1, будет равной, но обратной по знаку работе прямого процесса:

W12 = - W2-1; W12 + W2-1 = 0. (3.1)

Следовательно, обратимый процесс – это процесс, в результате которого система может возвратиться в исходное состояние без изменений в окружающей среде.

Значит, обратимые процессы протекают с бесконечно малыми скоростями. Только при этих условиях система в каждый момент времени будет находиться в состоянии, бесконечно мало отличающемся от равновесного. такие процессы называют равновесными, или квазистатическими.

Проведем процесс расширения 1 моль газа с конечной скоростью. при изменении давления на конечную величину (нижняя кривая) объем газа увеличивается также на конечную величину. Последовательно перейдем из состояния 1 в состояние 2. Графически этот процесс изображен ломаной линией. Работа расширения, которую при этом совершает газ, численно равна площади под ломаной линией. Она меньше, чем в предыдущем случае. Проведем процесс в обратном направлении. Здесь также давление будет увеличиваться на конечную величину (верхняя ломаная линия). Объем газа уменьшается и через некоторое время достигает равновесного состояния. Работа, которую при этом производит внешняя среда (работа сжатия), численно равна площади, ограниченной верхней ломаной линией, двумя ординатами Р1 и Р2 и отрезком на оси абсцисс V1 – V2 . Сопоставим диаграммы сжатия и расширения и отметим, что при изменении состояния газа с конечной скоростью работа обратного процесса по абсолютной величине больше работы прямого процесса:

|W1-2| |-W2-1|, (3.2)

W1-2 + W2-1 0. (3.3)

Возвращение системы из конечного состояния в начальное происходит по другому пути, и в окружающей среде остаются какие-то изменения.

Необратимый процесс – это процесс, после которого система не может возвратиться в исходное состояние без изменений в окружающей среде. При протекании необратимого процесса в каждый момент времени система не находится в состоянии равновесия. Такие процессы называются неравновесными.

Вывод: Все самопроизвольные процессы протекают с конечными скоростями и поэтому являются необратимыми (неравновесными) процессами.

Вывод: Работа, совершаемая системой в обратимом процессе, всегда больше, чем в необратимом:

Wобр Wнеобр. (3.4)

Все реальные процессы в той или иной мере могут приближаться к обратимым. Работа, производимая системой, достигает максимального значения, если система совершает обратимый процесс:

Wобр = Wmax. (3.5)

Работу, производимую системой при переходе из одного состояния в другое, в общем случае можно представить как сумму работы расширения и других видов работы (работы против электрических, поверхностных, гравитационных и т.п. сил). Сумму всех видов работы, производимой системой за вычитом работы расширения, называют полезной работой. Если переход системы из состояния 1 в состояние 2 был осуществлен обратимо, то работа этого процесса будет максимальной (Wmax), а работа за вычетом работы расширения – максимальной полезной работой (W'max):

Wmax = W'max + p V; (3.6)

W'max = Wmax - p V. (3.7)

Формулировка и математическое выражение второго начала термодинамики

Установление второго начала термодинамики связано с исследованиями французского военного инженера С. Карно (1824 г.) принципов действия тепловых двигателей, т.е. машин, превращающих теплоту в работу, с целью повышения их коэффициента полезного действия (КПД). Окончательно второе начало термодинамики было сформулировано Р. Клаузиусом в 1850 году и У. Томпсоном (лордом Кельвином) в 1851 году.

Существует несколько эквивалентных формулировок второго начала термодинамики:

1. Невозможен самопроизвольный переход тепла от тела менее нагретого к телу более нагретому (Р. Клаузис).

2. Невозможно превратить теплоту в работу, не производя никакого другого действия, кроме охлаждения источника тепла (У. Томпсон, М. Планк).

3. Вечный двигатель второго рода невозможен (В. Оствальд).

Вечным двигателем второго рода называют такую машину, единственным результатом действия которой было бы получение работы за счет теплоты окружающей среды.

В любой системе два произвольно выбранные состояния (1” и 2”) различаются тем, что процесс перехода из состояния 1 в состояние 2 протекает самопроизвольно, а обратный процесс перехода из состояния 2 в состояние 1 самопроизвольно не идет.

Отсюда можно заключить, что существует какой-то объективный критерий, позволяющий установить принципиальное различие между этими двумя состояниями системы.

Рассмотрим изолированную систему, состоящую из теплового резервуара, 1 моля идеального газа, заключенного в цилиндре с подвижным поршнем, и устройства, позволяющего за счет перемещения поршня совершать работу (рис. 3.2).

Рис. 3.2. Изолированная система, состоящая из теплового резервуара, 1 моля идеального газа, заключенного в цилиндре с подвижным поршнем, и устройства, позволяющего за счет перемещения поршня совершать работу

Предположим, что газ обратимо расширяется от объема V1 до V2 и совершает работу W1. Энергия на совершение работы передается в форме тепла из резервуара. совершаемая газом работа равна полученной от резервуара энергии Q1:

. (3.8)

Функция 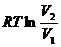определяется не только изменением объема, но и температурой. Разделим обе части уравнения на Т:

. (3.9)

Из равенства (3.9) видно, что изменения, происходящие в изолированной системе при протекании обратимого процесса, могут быть охарактеризованы величиной , которая определяется только исходным (V1) и конечным (V2) состоянием системы. Увеличение параметра в цилиндре с газом эквивалентно уменьшению этого параметра для теплового резервуара , т.е.

. (3.10)

При необратимом (самопроизвольном) расширении идеального газа от V1 до V2 (например, в вакууме, рис. 3.3) процесс происходит без совершения газом работы, так как Р=О и, соответственно, передача энергии от резервуара не происходит: Q=0, т.е. изменение внутренней энергии (U) для газа равно нулю.

Рис. 3.3. При самопроизвольном расширении идеального газа от V1 до V2 в вакууме процесс происходит без совершения газом работы, так как Р = О и,
соответственно, передачи энергии от резервуара не происходит: Q = 0,
т.е. изменение внутренней энергии ( U) для газа равно нулю

Однако состояние газа в резервуаре изменилось на величину , а состояние резервуара – нет. Поэтому в целом состояние системы изменилось на величину , т.е. , так как

. (3.11)

Таким образом, протекание самопроизвольного процесса в изолированной системе в общем случае связано с возрастанием некоего параметра состояния системы. Этот параметр получил название энтропии.

Из примера следует, что самопроизвольно в изолированной системе протекают те процессы, которые приводят к возрастанию энтропии системы.

Если энтропия системы в исходном состоянии может быть выражена как S1 = R ln V1, а в конечном состоянии S2 = R ln V2, то изменение энтропии в результате протекания обратимого процесса следующее:

S = S2 - S1 = R ln V2/V1,

или

S(обр.процесс) = . (3.12)

Соответственно для необратимого процесса (самопроизвольного)

S(необр.процесс) > . (3.13)

Справедливость последнего выражения следует из первого начала термодинамики.

В соответствии с I началом:

U = Q – W. (3.14)

Переведем систему из состояния 1 в состояние 2 обратимым и необратимым путем:

U(обр)=Qобр – Wобр, (3.15)

U(необр) = Qнеобр – Wнеобр. (3.16)

Если U является функцией состояния, то U(обр) = U(необр). Известно, что Wобр  Wнеобр, следовательно Qобр  Qнеобр. S не зависит от пути процесса, так как является функцией состояния, т.е. S(обр) = S(необр). Тогда

(3.17)

или в общем случае

; (3.18)

. (3.19)

Знак равенства относится к обратимым, неравенства – к необратимым процессам.

Изменение энтропии изолированной системы

Для изолированной системы Q = 0, так как система не обменивается с окружающей средой ни веществом, ни энергией, и

S  0. (3.20)

Для обратимого процесса

S = 0;

для необратимого энтропия системы увеличивается:

S  0. (3.21)

Какие бы процессы ни протекали в изолированной системе, ее энтропия не может уменьшаться.

Так как самопроизвольные процессы в изолированных системах идут с увеличением энтропии, то при достижении равновесия энтропия изолированной системы будет максимальной, а ее изменение равно нулю:

Sравн. = Smax, (3.22)

S = 0. (3.23)

Уравнения (3.22; 3.23) – критерии равновесия изолированных систем.

Статистическая природа второго начала
термодинамики

В то время как первое начало термодинамики является всеобщим законом природы, не знающим ограничений и применимым к любым системам, второе начало термодинамики представляет собой статистический закон, справедливый для макроскопических систем, состоящих из очень большого числа частиц (молекул, атомов, ионов), для которых применимы физические понятия, имеющие статистическую природу (например, как температура, давление).

Известно, что состояние и свойства любой макроскопической системы, состоящей из совокупности большого числа частиц, могут быть описаны с помощью статистической механики. Сущность статистического описания макросистем состоит в применении к совокупности большого числа частиц основных положений теории вероятности, а к отдельным частицам – законов классической механики.

С точки зрения статистической механики второе начало термодинамики, как это впервые было показано Л. Больцманом, сводится к утверждению: все самопроизвольные процессы в макроскопических системах протекают в направлении от менее вероятного к более вероятному состоянию системы.

Таким образом, процессы, запрещенные вторым началом, например самопроизвольный переход тепла от менее нагретого тела к более нагретому, оказываются не невозможными, а крайне маловероятными, вследствие чего они не наблюдаются.

Любое состояние системы характеризуется определенной термодинамической вероятностью, и чем больше последняя, тем ближе система к состоянию равновесия. В состоянии равновесия система обладает максимальной термодинамической вероятностью.

Л. Больцман предложил следующее уравнение, устанавливающее связь между энтропией S и термодинамической вероятностью :

S = k ln , (3.24)

где k – постоянная Больцмана, численно равная отношению газовой постоянной R к числу Авогадрo NA, т.е. ;  – термодинамическая вероятность системы, т.е. число микросостояний, которыми можно осуществить данное макросостояние системы.

Статистическая термодинамика показывает, что энтропия может рассматриваться как сумма составляющих, относящихся к различным формам движения частиц.

Принято группировать их по характеру движения частиц, рассматривая следующие составляющие энтропии: энтропию поступательного движения молекул (Sпост.), энтропию вращательного движения молекул (Sвращ.), энтропию вращательного движения атомов и атомных групп, содержащихся в молекуле (Sвн.вращ.), энтропию колебательного движения атомов и атомных групп (Sкол) и энтропию движения электронов (Sэл.).

Таким образом, энтропию можно представить как сумму следующих составляющих:

S = Sпост +Sвращ + Sвн.вращ + Sкол + Sэл. (3.25)

При этом некоторые из них можно рассматривать как сумму более частных составляющих. Так, Sкол. является суммой составляющих, относящихся к различным видам колебаний.

При рассмотрении обычных химических процессов не учитывают составляющие энтропии, связанные с состоянием атомных ядер (спиновой эффект) и с изотопным эффектом.

Для каждого данного вещества энтропия возрастает при всех процессах, вызываемых движением частиц (испарение, плавление, расширение газов, диффузия и пр.). энтропия возрастает при ослаблении связей между атомами в молекулах и при разрыве их, т.е. диссоциации молекул на атомы или атомные группы. Наоборот, с упрочением связей уменьшается энтропия.

Вместе с тем второе начало термодинамики не настолько простое в смысле его применения.

Рассмотрим, например, условия и задачу, которая была решена Клаузиусом в середине XIX века следующим образом. Если вселенная является изолированной системой, и энтропия в обратимых процессах не меняется, а в необратимых только возрастает, то это возрастание должно приводить к постепенному выравниванию температуры во всех ее частях. В плане вселенной это должно привести в конце концов к полному выравниванию температуры, т.е. к «тепловой смерти». Правомерность такого вывода рассматривается с разных сторон такими учеными, как М. Смолуховский, Я. Ван-дер-Ваальс и др. Можем ли мы в настоящее время на основе тех знаний, которые у нас есть, его оспорить?

Формулировка третьего начала термодинамики

В 1912 году М. Планк высказал постулат: при абсолютном нуле энтропия правильно образованного кристалла чистого вещества равна нулю.

Справедливость постулата Планка, называемого третьим началом термодинамики, следует из экспериментальных данных о зависимости теплоемкости кристаллических веществ от температуры, а также из статистического характера второго начала термодинамики. При абсолютном нуле данное макросостояние кристалла чистого вещества, кристаллическая решетка которого не имеет каких-либо дефектов, предельно упорядочено и может быть реализовано единственным способом. Следовательно, термодинамическая вероятность при абсолютном нуле равна 1:

S = k ln 1 S = 0. (4.1)

На основании постулата Планка можно вычислить абсолютное значение энтропии. Если , а , то , где С – молярная теплоемкость данного вещества.

Интегрируя последнее уравнение в пределах от абсолютного нуля до Т, получим:

(4.2)

или

S_T = . (4.3)

4.2. Абсолютные и стандартные значения энтропии

Энтропию S_T называют абсолютной энтропией. Она численно равна изменению энтропии при равновесном переходе 1 моля кристаллического вещества от абсолютного нуля до данной температуры.

Вычисление абсолютной энтропии по уравнению (4.3) возможно лишь в том случае, если известна зависимость теплоемкости данного вещества от температуры.

Абсолютную энтропию тела в стандартном состоянии при данном Т называют стандартной энтропией и обозначают через S⁰_T; чаще всего Т=298.15 °К и ее обозначают через S⁰₂₉₈:

Дата добавления: 2018-02-28; просмотров: 311; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!