Практ. зан № 15 Тема 14 Несобственные интегралы
1. А3 [10] 2366, 2269, 2378, 2394, 2395
2. Образцы решения задач
Вычислить несобственный интеграл
или установить его расходимость.
Решение. Имеем
.
2.2. Доказать, что интеграл 
сходится.
Решение. Так как 
при 
и интеграл
сходится, то исходный интеграл также сходится.
2.3. Вычислить несобственный интеграл 
.
Решение. Подынтегральная функция терпит бесконечный разрыв в точке 
. Следовательно, по определению
,
т.е. данный интеграл сходится.
2.4. Исследовать, сходится ли интеграл 
.
Решение. Подынтегральная функция терпит разрыв в точке 
. Очевидно, что при 
Так как несобственный интеграл
т.е. сходится, то сходится и исходный интеграл.
2.5. Вычислить координаты центра масс однородной плоской фигуры, ограниченной решениями 
, 
.
Решение.Из однородности и симметричности данной фигуры следует, что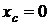 
. Для определения 
воспользуемся формулами:
, (1)
, (2)
где 
поверхностная плотность фигуры.
3. Д3 [10] 2367, 2370, 2377, 2396, 2400
Планы занятий в рамках самостоятельной работы студентов (СРСП)
Кредит-1. Линейная алгебра и аналитическая геометрия.
Тема: Определители и матрицы. Обратная матрица. Ранг матрицы и методы ее вычисления.
Тема: Система линейных алгебраических уравнений. Правило Крамера. Метод Гаусса.
Тема: Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Их свойства
|
|
|
и приложения.
Тема: Прямая на плоскости, плоскость и прямая в пространстве.
Тема: Кривые и поверхности второго порядка. Канонические уравнения эллипса, гиперболы и пара
болы.
Кредит-2. Дифференциальное исчисление функций одной переменной.
Тема: Введение в анализ. Функция. Предел функции.
Тема: Непрерывность. Сравнение функций. Вычисление пределов.
Тема: Производная и дифференциал..
Тема: Производные и дифференциалы высших порядков. Теоремы о среднем для дифференцируемых функций. Формула и ряд Тейлора.
Тема: Раскрытие неопределенностей. Исследование поведения функций и их графиков. Приложения дифференциального исчисления к геометрии.
Кредит-3. Интегральное исчисление функций одной переменной.
Тема: Неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица основных
интегралов. Метод подстановки. Интегрирование по частям.
Тема: Методы интегрирование некоторых классов. Интегралы, содержащие квадратных трехчлен.
Интегрирование рациональных, иррациональных, тригонометрических функций.
|
|
|
Тема: Определенный интеграл. Формула Нютона - Лейбница. Замена переменной. Формула интегри-
рования по частям.
Тема: Приложение определенного интеграла. Вычисление площади плоской фигуры, длина дуги пло-
ской кривой, объем тел вращения, площади поверхности вращения и работы переменной силы.
Тема: Несобственные интегралы.
2.5 Планы занятий в рамках самостоятельной работы студентов (СРС)
Кредит-1
Дата добавления: 2018-02-28; просмотров: 302; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!