Практ. зан. № 13 Тема 12 Определенный интеграл. Свойства . Формула Ньютона-Лейбница
1. А3[10] 2232, 2251, 2261, 2280, 2285
2. Образцы решения задач
2.1. Вычислить интеграл  .
.
Решение.  .
.
2.2. Вычислить интеграл  .
.
Решение.

 .
.
2.3. Вычислить интеграл  .
.
Решение.
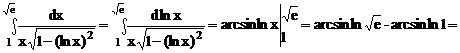
 .
.
2.4. Вычислить интеграл  .
.
Решение. Положим  . Если
. Если 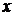 меняется от 0 до 1, то переменная
меняется от 0 до 1, то переменная  меняется от 0 до
меняется от 0 до  . На отрезке
. На отрезке  функция
функция  монотонна, непрерывна и имеет непрерывную производную. Применяя правило замены переменной в определенном интеграле, получим
монотонна, непрерывна и имеет непрерывную производную. Применяя правило замены переменной в определенном интеграле, получим
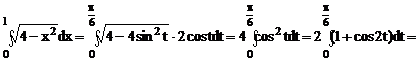
 .
.
2.5. Вычислить интеграл  .
.
Решение. Положим  ,
, 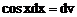 , тогда
, тогда  ,
,  . Тогда, применяя формулу интегрирования по частям, получим
. Тогда, применяя формулу интегрирования по частям, получим
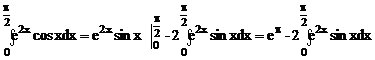 (*)
(*)
Последний интеграл еще раз проинтегрируем по частям, положив  ,
,  ,
,  ,
,  .
.
 .
.
Возвращаясь к равенству (*), имеем
 ,
,
и, перенося интеграл в левую часть равенства, получим
 , откуда
, откуда  .
.
3. Д3[10] 2233, 2245, 2264, 2279, 2286
Практ. зан. № 14 Тема 13 Приложение определенного интеграла.
1. А3 [10] 267, 2490, 2521, 2568, 2605, 2682
2. Образцы решения задач
2.1. Найти площадь фигуры, ограниченной параболой  и прямой
и прямой  .
.
Решение. Рассмотрим уравнение параболы:

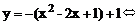
 .
.
Отсюда видно, что парабола симметрична относительно прямой  , ветвями направлена вниз и вершина ее лежит в точке (1,1).
, ветвями направлена вниз и вершина ее лежит в точке (1,1).
|
|
|
Вычертим данную параболу и прямую.

Совместным решением уравнений параболы и прямой определим абсциссы точек  и
и  . Имеем
. Имеем
 . Тогда
. Тогда

 (кв.ед.).
(кв.ед.).
Найти площадь фигуры, ограниченную первой аркой циклоиды
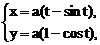
и отрезком оси абсцисс.
Решение. Начертим данную кривую

Точки  и
и  соответствуют значениям параметра
соответствуют значениям параметра  и
и  . Вычислим площадь фигуры:
. Вычислим площадь фигуры:

 (кв.ед.)
(кв.ед.)
2.3. Вычислить площадь, ограниченную кривой  (лемниската Бернулли).
(лемниската Бернулли).
Решение. Опишем кривую. Имеем  при
при  , т.е. кривая проходит через полюс. Из уравнения кривой видно, что полярный радиус
, т.е. кривая проходит через полюс. Из уравнения кривой видно, что полярный радиус  принимает вещественные значения, когда
принимает вещественные значения, когда  . Тогда
. Тогда
 ,
,  . При
. При 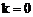 и
и  имеем
имеем
 ,
,  , откуда
, откуда  ,
,  .
.
Период функции  равен
равен  , поэтому при замене
, поэтому при замене  на
на  полярный радиус
полярный радиус  не изменяется, т.е. кривая симметрична относительно полюса
не изменяется, т.е. кривая симметрична относительно полюса  . Кривая так же симметрична относительно полярной оси
. Кривая так же симметрична относительно полярной оси  , т.к. для значений
, т.к. для значений  , отличающихся знаком,
, отличающихся знаком,  не изменяется. Начертим кривую.
не изменяется. Начертим кривую.
|

Учитывая симметрию, вычислим площадь фигуры, расположенной в первой четверти, т.е.  .
.
 (кв.ед.).
(кв.ед.).
2.4. Вычислить длину дуги кривой  от начала координат до точки
от начала координат до точки  .
.
Решение. Из уравнения кривой находим:  . Тогда длина дуги кривой равна:
. Тогда длина дуги кривой равна:
|
|
|

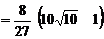 .
.
2.5. Вычислить длину дуги одной арки циклоиды  ,
,  .(рис.1)
.(рис.1)
Решение.

Параметр  изменяется от 0 до
изменяется от 0 до  , так как точка описывает одну арку циклоиды при одном обороте круга. Из уравнения циклоиды находим
, так как точка описывает одну арку циклоиды при одном обороте круга. Из уравнения циклоиды находим
 ,
,  ,
, 
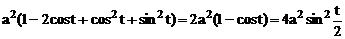 .
.
Тогда
 .
.
2.6. Вычислить длину кардиоиды  .
.
Решение. Так как кривая симметрична относительно полярной оси, то
при изменении  от 0 до
от 0 до  полярный радиус
полярный радиус  опишет половину кривой.
опишет половину кривой.
 |
Вычислим  . Тогда длина кардиоиды равна
. Тогда длина кардиоиды равна

 .
.
2.7. Найти объем тела, образованного вращением вокруг оси  одной арки циклоиды
одной арки циклоиды
 ,
,  .
.
Решение. Первой арке циклоида соответствует изменение параметра  от
от  до
до  . Тогда
. Тогда 


2.8. Вычислить работу, которую нужно затратить, чтобы растянуть пружину на 8 см., если известно, что для удлинения ее на 1см. необходимо приложить силу в 1кH.
Решение. Согласно закону Бука, сила  , растягивающая пружину, пропорциональна ее растяжению, т.е.
, растягивающая пружину, пропорциональна ее растяжению, т.е.  где
где  растяжение пружины (в метрах);
растяжение пружины (в метрах); 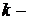 коэффициент пропорциональности. Так как по условию при
коэффициент пропорциональности. Так как по условию при  сил
сил  , то из равенства
, то из равенства  получаем
получаем  и
и  Следовательно, искомая работа
Следовательно, искомая работа
 ж.
ж.
2.9. Вычислить координаты центра масс однородной плоской фигуры, ограниченной линиями 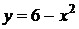 ,
,  .
.
|
|
|
Решение. Из однородности и симметричности данной фигуры следует, что 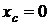 . Для определения
. Для определения  воспользуемся формулами:
воспользуемся формулами:
 (1)
(1)
 (2)
(2)
где  поверхностная плотность фигуры.
поверхностная плотность фигуры.



3.Д3 [10] 2455, 2491, 2522, 2572, 2606, 2683
Дата добавления: 2018-02-28; просмотров: 280; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

