Кредит-3. Интегральное исчисление функций одной переменной
Практ. зан. № 11. Тема 10 Неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица основных интегралов. Метод подстановки. Интегрирование по частям.
1. А3 [10] № 1676,16,85, 1686, 1687, 1693, 1706, 1721, 1698, 1699, 1771, 1773,1774,1842, 1838, 1847, 1850, 1860
2. Образцы решения задач
2.1. Вычислить интеграл 
Решение. Представляя интеграл алгебраической суммы в виде суммы интегралов, вынося постоянные множители за знаки интегралов и применяя формулы 1,2 таблицы основных интегралов, получим
 Здесь и далее произвольные постоянные, входящие в каждый из складываемых неопределенных интегралов, объединяются в одну произвольную постоянную.
Здесь и далее произвольные постоянные, входящие в каждый из складываемых неопределенных интегралов, объединяются в одну произвольную постоянную.
2.2. Вычислить интеграл 
Решение. Заменим единицу в числителе подинтегральной функции выражением  и применим формулы 7 и 8 таблицы интегралов
и применим формулы 7 и 8 таблицы интегралов


2.3. Вычислить интеграл 
Решение. Воспользуемся табличным интегралом

 полагая
полагая  , тогда
, тогда 
2.4. Вычислить интеграл 
2.5. Решение. Полагаем  , внесем функцию
, внесем функцию  под знак дифференциала, получим:
под знак дифференциала, получим:
 .
.
2.5. Вычислить интеграл 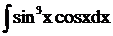 .
.
Решение. Внесем функцию  под знак дифференциала, т.е.
под знак дифференциала, т.е.  , обозначим
, обозначим  , тогда
, тогда
 .
.
2.6. Вычислить интеграл  .
.
Решение. Полагаем  ,
,  , тогда
, тогда
 ;
;  .Полагаем
.Полагаем  , так как достаточно иметь какую – либо одну первообразную. Итак,
, так как достаточно иметь какую – либо одну первообразную. Итак,  . Применяя формулу интегрирования по частям, получим:
. Применяя формулу интегрирования по частям, получим: 
 .
.
3. Д3 [10] № 1678, 1689, 1696, 1701, 1772, 1747, 1749, 1753, 1764, 1776, 1833, 1839, 1848, 1851
Практ. зан. № 12 Тема 11 Методы интегрирование некоторых классов функции.
|
|
|
1. А3 [10] 1800, 1796, 1805, 1940, 1943, 1952, 1944, 1950,2014,2068,1808,
2. Образцы решения задачи
2.1. Вычислить интеграл  .
.
Решение. Рассмотрим трехчлен знаменателя:

 .
.
Тогда

 .
.
2.2. Вычислить интеграл  .
.
Решение. Выделим полный квадрат из трехчлена:

 .
.
Тогда
 .
.
2.3. Вычислить интеграл  .
.
Решение. Вычислим производную знаменателя:  . Выделим двучлен
. Выделим двучлен  .
.



 .
.
2.4. Вычислить интеграл  .
.
Решение. Подынтегральная функция – неправильная рациональная дробь, поэтому выделим ее целую часть делением числителя на знаменатель


 .
.
Следовательно,
 .
.
Полученную справа правильную дробь разложим на простые дроби и учитывая, что  , получим
, получим
 . (5.1)
. (5.1)
Приводя правую часть к общему знаменателю и приравнивая числители, получим тождество
 (5.2)
(5.2)
Рассмотрим два способа нахождения неизвестных коэффициентов.
Первый способ. Метод частных значений.
Аргументу 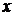 придают удобные значения (таковыми являются значения корней) и подставляют их в тождество (5.2). Отмечая за чертой слева значения, придаваемые аргументу
придают удобные значения (таковыми являются значения корней) и подставляют их в тождество (5.2). Отмечая за чертой слева значения, придаваемые аргументу 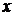 , получим:
, получим:




Второй способ. Метод неопределенных коэффициентов.
|
|
|
Коэффициенты при одинаковых степенях 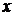 в обеих частях тождества (5.2) должны быть равны. Отметим слева за чертой при каких степенях
в обеих частях тождества (5.2) должны быть равны. Отметим слева за чертой при каких степенях 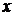 сравниваются коэффициенты, тогда
сравниваются коэффициенты, тогда


Из третьего уравнения системы находим  . Подставляя значение A в первое уравнение и сокращая второе на 2, будем иметь
. Подставляя значение A в первое уравнение и сокращая второе на 2, будем иметь

откуда  .
.
Итак,

 .
.
2.5. Вычислить интеграл  .
.
Решение. Выпишем показатели  :
:  . Общий знаменатель этих дробей равен 6, поэтому полагаем
. Общий знаменатель этих дробей равен 6, поэтому полагаем  , отсюда
, отсюда 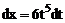 . Тогда
. Тогда



 .
.
2.6. Вычислить интеграл  .
.
Решение. Применяя универсальную подстановку  , получим
, получим
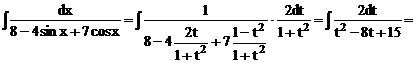

 .
.
3. Д3 [10] 1801, 1797, 1807, 1941, 1945, 1953, 1946, 2016, 2069, 1809,
Дата добавления: 2018-02-28; просмотров: 264; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
