Кредит-2. Дифференциальное исчисление функций одной переменной
Практ. зан. № 6 Тема № 5 Введение в анализ. Функция. Предел функции.
1. АЗ: [11], №№ 1.4,1.11, 1.18, 1.29, 1.44, 1.60, 1.80, 1.83, 1.95, 1.102, 1.106, 1.107, 1.108, 1.109,
1.113, 1.114, 1.126, 1.130, 1.141, 1.175, 1.177.
2. Образцы решения задач
2.1 Найти область определения функции 
.
Решение. Функция определена, если 
и 
, т.е. если 
и 
. Тогда 
.
2.2 Установить четность или нечетность функций:
1) 
; 2) 
; 3) 
;
4) 
; 5) 
.
Решение. 1) Заменяя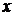 
на 
, получим
,
т.е.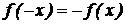 
. Следовательно, функция – нечетная.
2) Имеем 
, т.е. 
.
Итак, функция – четная.
3) Рассмотрим 
, т.е. . Следовательно, функция – четная.
4) Имеем 
. Таким образом 
и 
, т.е. данная функция не является ни четной, ни нечетной.
5) Рассмотрим
, т.е. .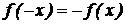
Следовательно, функция – нечетная.
2.3. Найти 
.
Решение.Здесь неопределенность вида 
.
Разделим числитель и знаменатель дроби на старшую степень 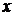, т.е. на 
:
= 
= 
.
2.4. Найти 
.
Решение:
разделим числитель и знаменатель на x
= 
2.5. Найти:
1) 
; 2) 
;
3) 
; 4) 
; 5) 
;
6) 
; 7) 
; 8) 
;
9) 
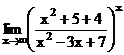; 10) 
.
Решение. 1) Используя первый замечательный предел, имеем
= 
= 
= 
.
2) Известно, что
.
Воспользуемся результатом предыдущего примера, приняв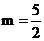 
.
= 
.
3) 
= 
.
4) Полагаем 
. Тогда 
при 
и
= 
= 
=
.
Заметим, что 
.
5) Используем замечательный предел
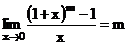при 
, тогда 
6) Преобразуем функцию так, чтобы использовать замечательный
предел:
.
|
|
|
= 
.
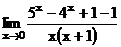7) Полагаем 
, тогда 
при 
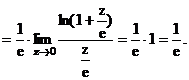
Воспользовались замечательным пределом
8) Имеем неопределенность вида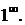 
В этом случае функция преобразуется так, чтобы использовать второй замечательный предел,
9) Делением числителя дроби на знаменатель выделим целую часть. Тогда,
= 
.
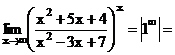
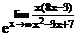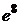10) 
.
Можно было также воспользоваться подстановкой 
3. ДЗ: [11], №№ 1.5, 1.12, 1.19, 1.30, 1.45, 1.61, 1.81, 1.84, 1.96, 1.103, 1.110, 1.111, 1.112,
1.115,1.125, 1.131, 1.142, 1.176.
Практ. зан. № 7 Тема 6 Непрерывность. Сравнение функций. Вычисление пределов.
1. АЗ: [11], №№ 1.213, 1.217, 1.223, 1.229, 1.231, 1.233, 1.235, 1.237, 1.264, 1.288, 1.290, 1.292, 1.303, 1.306, 1.310, 1.320, 1.322, 1.349, 1.351, 1.360, 1.366, 1.387, 1.389, 1.404.
2. Образцы решения задач
2.1 Сравнить бесконечно малые:
, 
, 
, 
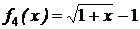
с бесконечно малой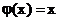 
.
Решение. 1) 
.
Следовательно, 
и 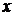одного порядка.
2) 
, 
1.
Следовательно,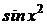 
является бесконечно малой высшего (второго) порядка.
3) 
, 
.
Следовательно, 
есть бесконечно малая низшего порядка (порядок равен 
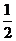) по отношению к х.
4) 
.
Следовательно, 
и х одного порядка.
2.2. Найти следующие пределы:
а) 
б) 
;
Решение. Числители и знаменатели дробей будем заменять эквивалентными бесконечно малыми.
а) 
~ 
, tg 8x ~ 8x, при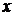 
, тогда 
.
б) 
~ , 
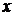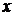~ , тогда 
.
2.3. Доопределить функцию 
в точке 
таким образом, чтобы она стала непрерывной в этой точке.
|
|
|
Решение. Функция 
не определена при . Вычислим односторонние пределы:
.
Следовательно, для непрерывности в точке 
полагаем 
. Итак, функция
,
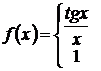
будет непрерывной в точке 
.
В следующим примере найти точки разрыва функций.
Решение. Каждая из трех функций 
непрерывны в области определения. Поэтому разрыв возможен только на стыке промежутков, то есть в точке . Вычислим
Следовательно, является точкой разрыва второго рода.
3. ДЗ: [11], №№ 1.214, 1.218, 1.224, 1.230, 1.234, 1.236, 1.265, 1.289, 1.291, 1.304, 1.311, 1.321, 1.350, 1.361, 1.367, 1.388, 1.405.
Практ. зан. № 8 Тема 7 Производная и дифференциал.
1. АЗ: [11], №№ 5.1, 5.5, 5.9, 5.17, 5.21, 5.23, 5.25, 5.27, 5.37, 5.41, 5.53, 5.61, 5.63, 5.69, 5.81, 5.83, 5.85, 5.94, 5.144, 5.146, 5.148, 5.164, 5.168, 5.170, 5.172, 5.184, 5.186, 5.192, 5.197, 5.290, 5.296, 5.303, 5.312.
2. Образцы решения задач
2.1 Найти 
и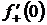 
для функции 
Решение: Имеем по определению
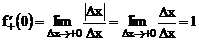
Заметим, что функция не имеет производной в точке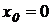 
2.2 Найти производную функции 
.
Решение: Полагая 
и 
, имеем 
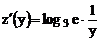и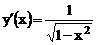 
. Отсюда получаем 
.
2.3 Найти 
, если 
, 
Решение:Имеем
.
2.4 Пользуясь определением производной функции, найти производную функции 
в точке 
Решение. Дадим значению 
приращение 
Тогда функция 
получит приращение:
|
|
|
Найдем:
Итак, 
.
2.5 Составить уравнения касательной и нормали к кривой 
в точке (2,3).
Решение 
Напишем уравнение пучка прямых, проходящих через данную точку (2,3) 
Вычислим: 
Тогда, для касательной: 
для нормали 
Подставляя эти значения в уравнение пучка прямых, получим
уравнение касательной 
или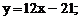 
уравнение нормали 
или 
2.6 Найти производную: 
Решение.Преобразуем функцию 
.
Тогда
.
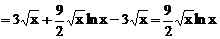2.7 Найти 
если 
Решение. 
Вычислим: 
Тогда 
2.8 Найти 
если 
Решение.Находим 
Тогда
2.9 Найти вторую производную функции, заданной параметрическим уравнением: 
.
Решение: В соответствии с формулами имеем:
3. ДЗ: [11], №№ 5.2, 5.10, 5.11, 5.22, 5.26, 5.38, 5.54, 5.62, 5.70, 5.82, 5.86, 5.95, 5.145, 5.147, 5.165, 5.169, 5.171, 5.185, 5.193, 5.198, 5.291, 5.304, 5.305, 5.313.
Дата добавления: 2018-02-28; просмотров: 272; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!