КОНТРОЛЬНАЯ РАБОТА ПО РАЗДЕЛУ «ДИНАМИКА»

Задача 3.1

Задание относится к прямой задаче динамики точки: по известным (заданным) силам и начальным условиям движения требуется определить движение точки, получив уравнения движения. Для этого следует изобразить движущееся тело (точку) в произвольный момент времени, показать все действующие на тело (заданные) силы, освободиться от связей, заменив их действие соответствую-щими реакциями. Затем составить дифференциальные уравнения движения (два при криволинейном и однопри прямолинейном движениях) и проинтегрировать их. Значения постоянных интегрирования определить из начальных условий. Исходные данные для различных вариантов даны в табл. 3.1., а схемы приведены на рис. 3.1.

Таблица3.1

Цифрашифра	1-яцифрашифра			2-яцифрашифра			3-яцифрашифра
	v0, м/с	a, м	b, м	a,град	Силы, Н		Номерусловия	Номерсхемы (рис.4.1)	f
					F	P
1	21	4,5	1,0	30	2	30	3.1.1	1	–
2	22	5,0	1,5	45	4	35	3.1.1	2	–
3	23	5,5	2,0	60	6	40	3.1.1	3	–
4	24	6,0	2,5	30	8	45	3.1.1	4	–
5	25	6,5	3,0	45	10	50	3.1.2	5	–
6	26	7,0	3,5	60	12	55	3.1.2	6	–
7	27	7,5	4,0	30	14	60	3.1.3	7	0,10
8	28	8,0	4,5	45	16	65	3.1.3	8	0,12
9	29	8,5	5,0	60	18	70	3.1.4	9	0,14
0	30	9,0	5,5	30	20	75	3.1.4	10	0,16

Условия

1. Тяжелая материальная точка М брошена под углом a к горизонту со скоростью v₀. В начальный момент времени точка находилась в положении М₀. Пренебрегая сопротивлением среды, определить уравнения движения точки в заданной системе координат (см. рис. 3.1, схемы 1 – 4).

2. Тело М весом Р брошено вертикально вверх (см. рис. 3.1, схема 5) или вниз (см. рис. 3.1, схема 6) со скоростью v₀. При движении на тело действует сила ветра F. В начальный момент тело находилось в положении М_о. Определить уравнение движения, приняв его за материальную точку, в заданной системе координат (см. рис. 3.1, схемы 5, 6).

3. Груз весом Р движется прямолинейно по горизонтальной плоскости. На груз действует сила F, составляющая с горизонталью угол a. Коэффициент трения скольжения груза о плоскость равен f. В начальный момент времени груз находился в положении М_о на расстоянии a от начала координат и имел скорость v₀. Определить уравнение движения груза в заданной системе координат (см. рис. 3.1, схемы 7, 8).

4. Груз весом Р движется вверх (см. рис. 3.1, схема 9) или вниз (см. рис. 3.1, схема 10) по шероховатой наклонной плоскости. Коэффициент трения скольжения груза о плоскость равен f. В начальный момент груз находился в положении М_о на расстоянии a от начала координат и имел скорость v₀. Определить уравнение движения груза в заданной системе координат (см. рис. 3.1, схемы 9, 10).

Примечание. Для схем 8 и 9 определить уравнение движения груза на первом этапе, когда движение происходит в направлении начальной скорости.

Рис.3.1. Схемы к задаче 3.1

Пример решения задачи 3.1.

Условие. Груз весом Р движется вниз по шероховатой наклонной плоскости, составляющей угол a=30°с горизонтом. Коэффициент трения скольжения груза о плоскость f=0,16. В начальный момент груз находился в положении М_о на расстоянии a=9 м от начала координат и имел скорость v₀=30 м/с. Определить уравнение движения груза в заданной системе координат (рис. 3.2).

Рис. 3.2

Решение. 1. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (шероховатой наклонной плоскости), заменив ее действие нормальной составляющей реакции N и силой трения F_тр. Тогда тело будет двигаться под действием системы трех сил (Р, N,F_тр).

1. Примем тело за материальную точку. Проектируя основноеуравнение динамики точки 

на оси декартовых координат Оx и Оy (ось Оx совпадает с направлением движения точки), получим два дифференциальных уравнения:

    Здесь m – масса точки; – проекции ускорения точки на соответствующие оси.

Так как тело движется прямолинейно вдоль оси Оx, то проекция ускорения на ось Оy равна нулю, следовательно, уравнение (3.2) примет вид .

Сила трения по закону Кулона равна . С учетом этого выражения дифференциальное уравнение (3.1) примет следующий вид:

.

После замены , где – ускорение свободного падения тела, и очевидных преобразований получим следующее дифференциальное уравнение второго порядка:

.

Для понижения порядка уравнения произведем замену , получим дифференциальное уравнение первого порядка с разделяющимися переменными:

.

Разделив переменные, проинтегрируем дифференциальное уравнение с учетом начальных условий (при t=0,v_x=v₀):

Произведем замену для понижения порядка уравнения  и, разделив переменные, проинтегрируем дифференциальное уравнение второй раз с учетом начальных условий (при t=0 x=x₀=a):

Подставив в соотношение (4.4) значения заданных величин, получим окончательно следующее уравнение движения груза:

Задача 3.2

Данная задача на определение скорости материальной точки решается с применением теоремы об изменении количества движения.

Телу массой m сообщена начальная скорость v₀, направленная вверх по наклонной плоскости, составляющей угол α с горизонтом. На тело действует сила P, направленная в те же сторону (рис. 3.3).

Рис.3.3

Зная закон изменения силы Р=Р(t) и коэффициент трения скольжения f, определить скорость тела в момент времени t₁ ,t₂ , t₃ и проверить полученный результат для момента времениt₁ с помощью дифференциального уравнения движения.

Необходимые для решения данные приведены в таблице 3.2

Таблица3.2 .

Цифрашифра	1-я цифрашифра							2-я цифрашифра									3-я цифрашифра
	m, кг	v0, м/с		t1, с		t2, с	t3, с	P0, Н		P1, Н			P2, Н				P3, Н			α, град	f
1	35	5,4		4		10	16	100	200			150			250				25			0,10
2	20	3,0		6		10	15	200	100			160			180				37			0,25
3	25	4,0		4		10	16	200	200			120			200				21			0,10
4	10	4,5		5		10	16	140	180			140			100				32			0,12
5	16	9,0		4		8	16	120	120			120			160				24			0,08
6	40		4,0		4	9	12	400	300			300		140					40			0,06
7	20		8,0		5	8	11	300	300			150		180					25			0,20
8	16		7,6		6	11	13	275	200			160		120					23			0,12
9	12		5,0		6	10	14	100	140			120		110					20			0,20
0	50		12,0		2	6	12	150	300		200					200		27			0,08

 

При построении графика изменения силы Р по заданным её значениям Р₀, Р₁, Р₂, Р₃ для момента времени t₀,t₁ , t₂ , t₃, считать зависимость Р=Р(t) между указанными моментами времени линейной. Значение силы Р, задаваемое по табл. 3.2 в виде дроби, указывает на то,что модуль силы в заданный момент времени претерпевает «скачок»: в числителе указан модуль силы в конце промежутка времени, а в знаменателе – в начале следующего промежутка времени.

Пример решения задачи 3.2.

Дано: m=40 кг, v₀=10 м/с, t₂=8 с, Р₀=0, t₃=12 с, Р₁=250 Н, Р₂=300/200 Н, α=30°, f=0,1.

Определить v₁,v₂, v₃и t₁, t₂, t₃.

Решение

Покажем силы, действующие на тело (рис. 3.3): вес , нормальную реакцию плоскости , силу трения скольжения , направив её противоположно начальной скорости, т.е. вниз по наклонной плоскости.

Построим график Р=Р(t) по заданным значениям Р₀, Р₁, Р₂, Р₃(рис. 3.4)

Рис. 3.4.

 1. Для тела, принимаемого за материальную точку, составим уравнение, выражающее теорему об изменении количества движения в проекциях на ось Х для промежутка времени от 0 до t:

mv_1x-mv_ox=ΣS_ix;

гдеΣS_ix=Gt₁ - Ft₁ + S_px.

 

Проекция импульса переменной силы Р за t₁ с:

S_px= .

Этот интеграл определяется как площадь треугольника ОВМ на графике Р=Р(t):

S_px= =375Н с

Учитывая, что сила трения скольжения F=fN=fGcosα, получаем уравнение (1) в следующем виде:

mv_1x-mv_0x=-gt₁ sinα-fgcosαt₁+375,

откуда

v_1x=v_0x-gt₁ sinα – fgcosαt₁+  ,

т.е. v_1x=10-9,81 3 0,5-0,1 9,81 0,87 3+ =10-14,72-2,76+9,38=2,10 м/с ,

таким образом, v₁= v_1x=2,10 м/с.

2. Для определения скорости тела в момент времени t₂ составим уравнение, выражающее теорему об изменении количества движения, для промежутка времени t₂-t₁:

mv_2x-mv_1x= ΣS_ix

где ΣS_ix=-G(t₂-t₁) -F(t₂-t₁)+S_px.

Проекция импульса переменной силы Р за (t₂-t₁) с выражается площадью трапеции МВСLS на графике Р=Р(t):

S_px= - =1375 Н

Поэтому уравнение имеет вид

mv_2x-mv_1x=-mg(t₂- t₁)sinα -fmgcosα(t₂- t₁)+1375,

откуда

v_2x=v_1x-g(t₂- t₁)sinα – fgcosα(t₂- t₁)+ =

=2,10-9,81 0,5-0,1 9,81 0,87 5+ =2,10-24,52-4,27+34,38=7,68 м/с .

Таким образом,

v₂=v_2x=7,68 м/с .

3. Уравнение, выражающее теорему об изменении количества движения и составленное для промежутка времени t₃-t₂, дает возможность определить скорость телаv₃в момент t₃:

mv_3x-mv_2x= ΣS_ix

где ΣS_ix=-G(t₃-t₂) -fGcos  (t₃-t₂)+S_px.

Проекция импульса переменной силы Р за (t₃-t₂) с выражается площадью трапеции УDEK :

S_px= =700 Н

тогда                    v_3x=v_2x-g(t₃- t₂)sinα – fgcosα(t₃- t₂)+ =

=7,68-9,81 0,5-0,1 9,81 0,87 4+ =7,68-19,62-3,41+17,5=2,15 м/с .

Таким образом,                v₃=v_3x=2,15 м/с.

Задача 3.3.

На звено 1 механизма, угловая скорость которого равна , с некоторого момента времени (t=0) начинает действовать пара сил с моментом M (движущий момент) или движущая сила Р.

Массы звеньев 1 и 2 механизма равны соответственно m₁ иm₂, а масса поднимаемого груза 3 – m₃. Момент сил сопротивления вращения ведомого звена 2 равен М_С. Радиусы больших и малых окружностей звеньев 1 и 2: R₁, r₁, R₂, r₂.

Схемы механизмов показаны на рис.3.5, а необходимые для реше­ния данные приведены втабл.3.3.

Haйти: уравнение вращательного движения звена механизма, указанного в последней графе табл.3.3. Определить также натяжение нитки в заданный момент времени, а в вариантах, где имеется соприкасание звеньев 1 и 2, найти, кроме того, окружное усилие в точке их касания. Звенья 1 и 2, для которых радиусы инерции  и  в табл.3.3 не заданы, считать сплошными однородными дисками.

Рис.3.5.

Таблица 3.3.

Цифрашифра	1-я цифрашифра					2-я цифрашифра				3-я цифрашифра						Номерсхемы
	m1, кг	m2, кг	m3, кг	R1, см	r1, см	R2, см	r2, см	iх1*, см	iх2*, см	M1, Нм	P1, Н	Mс, Нм	w10, с-1	t1, с	*
1	100	300	500	20	40	60	40	50	50	2100+20t	-	1000	2	2	1		1
2	300	80	500	70	50	40	30	60	-	1800+40t	t	600	0	0.5	2		2
3	200	100	400	60	30	30	20	60	20	t	3000+100t	800	0.5	2.5	1		3
4	100	250	300	20	60	50	30	50	40	-	2700+200t	1400	1.5	2	1		4
5	150	300	600	30	30	50	20	50	30	-	5500+200t	1500	2	1	2		5
6	400	250	600	70	20	30	20	70	20	4800+10t	-	800	3	4	1		6
7	300	200	400	60	40	30	20	50	20	-	3000+100t	500	0	3	2		7
8	300	250	700	50	30	40	20	40	30	-	9700+50t	500	1	2	1		8
9	200	100	500	80	60	40	20	50	-	5900+30t	-	600	2	3	2		9
0	250	100	400	40	20	30	20	30	-	-	500+100t	1200	0	1.5	2		10

Примечание:

1. Звёздочками (xx) обозначено звено, для которого нужно определить уравнение вращательного движения.
2. Радиусы инерции звеньев 1 и 2 i_X1, и i_X2, заданы относительно осей вращения этих звеньев.

Пример решения задачи 3.3

Пусть: m₁ =100, m₂= 150, m₃ = 400 кг, М=4200+200tНм,М_С =2000 Нм = соnst,

R₁=60, R₂=40 cм, r₂=20 cм, i_x1=20√2, i_xb= 30см, w₁₀= 2c^-1.

Найти уравнение вращательного движения звена второго механизма), а также окружное усилие S в точке касания звеньев 1 и 2 и натяжение нити Т в момент времени t₁ (рис.3.6) .

Решение

К звену 1 механизма приложена сила тяжести , движущий момент М, составляющие реакции подшипника ,  , окружное усилие  и нормальная реакция  звена 2.

 К звену 2 механизма приложена сила тяжести  , момент сил сопротивления , составляющие реакции подшипника , , натяжение нити Т , к которой подвешен груз 3, окружное усилие   и нормальная реакция   звена 1.

К грузу 3 приложена сила тяжести 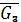, и натяжение нити Т.

Рисунок 3.6.

 

Очевидно: = - , = -  и .

Составим дифференциальное уравнение вращения звена 1 вокруг неподвижной оси :   

=  .

Главный момент  внешних сил, приложенных к звену 1 относительно оси   

Момент М приводит в движение систему и поэтому принят положительным, а момент, создаваемый усилием  , препятствует вращению звена 1 и, следовательно, отрицателен.

Дифференциальное уравнение вращательного движения звена 1 примет вид                        .

Выразим угловое ускорение  звена 1 через угловое ускорение  звена 2.

Так как            , то           .

Тогда уравнение принимает следующий вид:

Для составления дифференциального уравнения вращения вокруг оси   звена 2 , к которому подвешен груз 3, применим теорему об изменении кинетического момента

Кинетический момент системы 2-3 относительно оси

,

где  - кинетический момент звена 2, вращающегося с угловой скоростью вокруг неподвижной оси ;

 - момент количества движения груза 3 , движущегося поступательно со скоростью V. Так как V= ,

,

где   - приведённый к оси  момент инерции системы 2-3.

Главный момент

 

Момент, создаваемый усилием , приводит к движению системы 2-3 и поэтому принят положительным, а момент силы тяжести груза 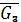  и момент сил сопротивления  препятствует движению системы и, следовательно, отрицательны.

Таким образом, получаем

Дифференциальное уравнение вращения звена 2:

=  .

В полученной системе уравнений

Неизвестные усилия  и угловое ускорение . Исключим , для чего первое уравнение этой системы умножим на  , второе на  и сложим соответствующие части уравнений:

() ,

Отсюда   .

Данное выражение определяет в общем виде угловое ускорение звена 2 механизма.

Учитывая исходные данные, найдём:

 = 100 (0,2 )² = 8 кг м²,

      = +  = 150·0,3² + 400·0,2² =29,5 кг м²

тогда    

Интегрируем это выражение дважды:

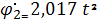+ 0,4597t+ ; 0,672 t³ + 0,230 t² + C₁t + C₂

Для определения постоянных интегрирования используем начальные условия задачи: при t = 0; = 0;

 2 ·  = 3

Следовательно, = С₁ ; = С₂ , т.е. С₁ = 3 с^-1 , С₂ = 0.

Уравнение угловой скорости звена 2 имеет вид

 2,017·t² + 0, 4597·t + 3, с^-1 .

Искомое уравнение вращательного движения звена 2 имеет вид

 0,672·t³ + 0,230·t² + 3t, рад.

Окружное усилие S можно определить из уравнения:

 , при t = 1 c

Рис. 3.7.

S =

                                                             =

Рис.11.5

Для определения натяжения нити Т составим дифференциальное уравнение вращения звена 2 в следующем виде (Рис.3.6):

= , из которого   T= , 

при t = 1 c

Рис. 11.5.

Т=

Задача3.4.

Данная задача решается с применением теоремы об изменении кинетической энергии механической системы. Прежде всего, требуется определить систему, т.е. перечислить те тела, которые включены в состав системы. Затем нужно изобразить систему в произвольный момент времени, показать все силы (заданные и реакции связей), действующие на тела системы, определить скорости тел и перемещения точек приложения сил. После этого необходимо вычислить кинетическую энергию системы в начальном и конечном положениях, вычислить работу всех сил на заданных перемещениях и подставить полученные результаты в формулу, выражающую теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме. Исходные данные приведены в табл. 3.4., а схемы- на рис. 3.8.

Условие

Однородный каток В весомQ и радиусом R соединен гибкой нерастяжимой и невесомой нитью с грузом А весом Р (см. рис. 3.8).

Таблица 3.4.

Цифрашифра	1-яцифрашифра			2-яцифрашифра			3-яцифрашифра
	r, см	S, м	M, Н м	Силы, кН			Номерсхемы (рис.12.5)	a, град	f
				P	Q	F
1	12	2,1	120	1,1	3,1	8,1+0,5S	1	30	0,06
2	14	2,2	140	1,2	3,2	8,2+0,4S	2	45	0,07
3	16	2,3	160	1,3	3,3	8,3+0,3S	3	60	0,08
4	18	2,4	180	1,4	3,4	8,4+0,2S	4	30	0,09
5	20	2,5	200	1,5	3,5	8,5+0,1S	5	45	0,10
6	22	2,6	220	1,6	3,6	8,6+0,5S	6	60	0,06
7	24	2,7	240	1,7	3,7	8,7+0,4S	7	30	0,07
8	26	2,8	260	1,8	3,8	8,8+0,3S	8	45	0,08
9	28	2,9	280	1,9	3,9	8,9+0,2S	9	60	0,09
0	30	3,0	300	2,0	4,0	9,0+0,1S	10	30	0,10

Рис. 3.8. Схемы к задаче 3.4

Нить переброшена через невесомый блок О радиусом r. К оси С катка (см. рис.3.8, схемы 1–5) или к грузу А (см. рис.3.8, схемы 6–8) или к свободному концу нити (см. рис.3.8, схемы 9,10) приложена сила F, линейно зависящая от величины перемещения S. Каток катится без скольжения; коэффициент трения скольжения груза о плоскость равен f, момент сил сопротивления в подшипнике блока – М. Определить скорость груза А, когда он переместится на величину S. В начальный момент система находилась в покое.

Пример решения задачи 3.4.

Условие. Однородный каток В весомQ=4 кН и радиусом R и груз А весом Р=2 кН, соединенные гибкой нерастяжимой и невесомой нитью, помещены на шероховатую поверхность, наклоненную к горизонту под углом a=30⁰  (рис. 3.9). Нить переброшена через невесомый блок О радиусом 30 см. К свободному концу нити приложена сила F, линейно зависящая от величины перемещения s: F=9,0+0,15×s (кН). Каток катится без скольжения; коэффициент трения скольжения груза о плоскость f=0,1, момент сил сопротивления в подшипнике блока М=300 Н м. Определить скорость груза А, когда он переместится на величину s=3 м. В начальный момент система находилась в покое.

Рис. 3.9

Решение. Формула, выражающая теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме, имеет вид

                                               (1)

где T, T₀– кинетическая энергия системы соответственно в конечный и начальный моменты времени;

– суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.

В рассматриваемой задаче система состоит из катка, груза, блока и нити. Система сил, действующих на систему, включает активные силы Q, P, F, реакции связей N_A, N_B, F_сц, F_тр, R_x, R_y и момент трения в блоке M.

Найдем сумму работ всех внешних сил системы на соответствующих перемещениях точек их приложения:

Работы сил N_А и N_B равны нулю, так как направления этих сил составляют прямой угол с направлениями перемещений точек их приложения. Работа силы сцепления F_сц и работы реакций R_x и R_у равны нулю, так как эти силы приложены к неподвижным точкам. Работы сил F, Р, Q, F_тр и пары сил с моментом М определим следующим образом:

После суммирования получим

.    (2)

Рассматриваемая механическая система состоит из абсолютно твердых тел, соединенных идеальной нитью. Для таких систем с идеальными связями сумма работ всех внутренних сил равна нулю

.                                               (3)

Рассчитаем кинетическую энергию системы в начальном и конечном положениях.

По условию задачи система в начальный момент находилась в покое, следовательно, ее кинетическая энергия в этот момент равна нулю T₀=0.

Кинетическая энергия груза А, движущегося поступательно, равна

,

где – масса груза А; – скорость груза.

Кинетическая энергия катка В, совершающего плоское движение, равна

,

где  – масса катка В;

v_C– скорость центра масс С катка, ;

– момент инерции катка относительно оси, проходящей через его центр масс;

w_В – угловая скорость катка, .

Кинетическая энергия системы равна сумме кинетических энергий всех тел, входящих в нее:

      (4)

Подставляя выражения (2) – (4) в формулу (1), выражающую теорему об изменении кинетической энергии системы, получим

,

откуда искомая скорость груза А, в момент, когда он переместится на расстояние 3 м, равна

Литература

Основная:

1. Никитин Н.Н. Курс теоретической механики: Учеб. для втузов.- СПб.: Лань, 2011. -720 с.- Режим доступа: http://e.lanbook.com/view/book/1807/.

 

Дополнительная:

2. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов / 19-е изд., стер.- М.: Высш.шк., 2009. - 416 с.

3. Мещерский И.В. Задачи по теоретической механике: Учебное пособие, 50-е изд., стер. / Под ред. В.А. Пальмова, Д.Р. Меркина.- СПб.: Издательство «Лань», 2010.- 448 с.

4. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах: Учеб. пособ. – М.: Политехника, 1995 – 670с.

5. Голубев Ю.Ф. Основы теоретической механики: Учеб. для вузов. – М.: Изд-во МГУ, 1992. - 524 с.

6. Сборник задач по теоретической механике: Учеб. пособие для студентов вузов / Будник Ф.Г., Зингерман Ю.М., Зеленский Е.И.; под ре. Кельзона А.С. – Высш. шк., 1987. – 176 с.

7. Никитин Е.М. Теоретическая механика для техникумов.- 12-е изд., испр.- М.: Наука. Гл.ред.физ.-мат.лит., 1988.- 336 с.

8. Техническая механика: Учеб. для техникумов / Эрдеди А.А. и др.- 2-е изд. перераб.- М.,Высш. школа, 1980.- 446 с.

 

 

Задания и методические указания

к выполнению контрольных работ по дисциплине

«Теоретическая механика»

 

 

Подписано в печать         . Формат 60х84/16. Бумага для множ. аппаратов. Печать плоская. Усл. печ. л. ____ . Уч.- изд. л.___ . Тираж____ экз. Заказ____     

ФГАОУ ВПО «Российский государственный профессионально-педагогический университет, Екатеринбург, ул. Машиностроителей, 11.

Ризограф ФГАОУ ВО РГППУ. Екатеринбург, ул. Машиностроителей, 11.

---

Дата добавления: 2018-02-28; просмотров: 655; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!